
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальный закон распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Этот закон наиболее часто встречается на практике. Он является предельным законом, к которому приближаются другие законы распределения. Нормальное распределение является одним из самых важных распределений в статистике. Обычно всё сравнивают с нормальным законом распределения. Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами µ и σ2, если ее плотность вероятности имеет вид:
Свойства плотности распределения вероятностей: Она колоколообразная ("колокол Гаусса"), иначе унимодальная. Плотность определяется двумя параметрами: математическим ожиданием (µ) и средним квадратическим отклонением (σ). Симметричная относительно среднего. Среднее и медиана нормального распределения равны. Кривая сдвигается вправо, если среднее увеличивается при постоянном квадратическом отклонении (рис. 11.56), и сдвигается влево, если среднее уменьшается. Кривая расширяется, если среднее квадратическое отклонениеσ увеличивается (если среднее постоянно). Кривая становится более остроконечной с меньшей шириной основания колокола, σ если уменьшается при среднем постоянном (площадь под графиком всегда равна 1) (рис. 11.5в).
Рис. 12.5. Кривая нормального закона распределения и ее изменение при изменении параметров Дополнительные свойства: Вероятность того, что нормально распределенная случайная величина X со средним µи средним квадратическим отклонением σ(стандартное отклонение) находится между (µ-σ) и (µ+σ), равна 0,68, т.е. 68% случайной величины X отличается от среднего не более чем на одно стандартное отклонение ± σ(рис. 11.6). Вероятность того, что нормально распределенная случайная величина X находится между (µ-2σ) и (µ+2σ), равна 0,95, т.е. примерно 95% случайной величины X отличается от среднего на два стандартных отклонения ±2σ (рис.11.6). Вероятность того, что нормально распределенная случайная величина X находится между (µ-3σ) и (µ+3σ), равна 0,99, т.е. 99% (практически достоверно). Это свойство носит название правило трех сигм (рис. 12.6).
Рис. 12.6. Правило трех сигм Пример 8. Построить графики для случая µ2>µ1; σ2>σ1. Решение. Рис. 11.5 г. Варианты заданий №12.1. Случайная величина X задана законом распределения:
Найти математическое ожидание и среднее квадратическое отклонение. Построить многоугольник распределения. №12.2. Найти дисперсию случайной величины X, зная закон ее распределения. Построить многоугольник распределения.
№12.3. Дискретная случайная величина X имеет закон распределения.
Чему равна вероятность Р4(X=0,8)? Построить многоугольник распределения. Найти математическое ожидание и дисперсию. №12.4. Дискретная случайная величина X имеет закон распределения.
Найти вероятность Р1(х = 3) и P3(х = 5), если известно, что Р3 в 4 раза больше Р1. Построить многоугольник распределения. Найти математическое ожидание и дисперсию. №12.5. Дискретная случайная величина x – число мальчиков в семьях с 3 детьми. Предполагая равновероятными рождения мальчика и девочки: а) составьте ряд распределения числа рождений мальчиков; б) постройте многоугольник распределения. №12.6. 2 стрелка стреляют по одной мишени, делая независимо друг от друга по 2 выстрела. Вероятность попадания в мишень для первого стрелка равна 0,5, для второго – 0,6. Найдите закон распределения случайной величины x, равной общему числу попаданий в мишень. №12.7. Дискретная случайная величина x задана таблицей распределения:
Найдите функцию распределения F(x) и, используя ее, найдите вероятность события №12.8. Случайная величина X имеет плотность вероятности
Найдите функцию распределения F(x) и вероятность события №12.9. Плотность вероятности случайной величины x, распределенной равномерно на отрезке
Найдите математическое ожидание величины x. №12.10. Даны все возможные значения дискретной случайной величины X: x1 =1, x2= 2, x3= 3, а также известны №12.11. Найдите математическое ожидание и среднее квадратическое отклонение случайной величины x, имеющей плотность вероятности
Пользуясь правилом «трех сигм», укажите интервал, симметричный относительно математического ожидания, в который попадает случайная величина x с вероятностью 0,9973.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (см. рис. 12.5а).
(см. рис. 12.5а).

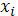
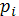
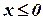 . Постройте график функции F(x).
. Постройте график функции F(x).

 , имеет вид:
, имеет вид: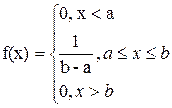
 Найдите закон распределения величины x.
Найдите закон распределения величины x. .
.


