
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача №1. Нормальный закон распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ. 2 ВВЕДЕНИЕ. 3 1 ЗАДАНИЕ И ИСХОДНЫЕ ДАННЫЕ. 4 1.1 Содержание задания. 4 1.2 Исходные данные. 5 2 ХОД ВЫПОЛНЕНИЯ РАБОТЫ.. 7 2.1 Задача №1. Нормальный закон распределения. 7 2.1.1 Гистограмма распределения. 7 2.1.2 Выборочные числовые характеристики. 9 2.1.3 Метод максимального правдоподобия. 10 2.1.4 Доверительные интервалы.. 11 2.2 Задача №2. Показательный закон распределения. 16 2.2.1 Гистограмма распределения. 16 2.2.2 Выборочные числовые характеристики. 19 2.2.3 Метод моментов. 19 2.2.4 Доверительные интервалы.. 19 2.2.5 Критерий Пирсона. 20 2.3 Задача №3. Случайный вектор. 22 2.3.1 Выборочные числовые характеристики. 22 2.3.2 Гипотеза о независимости. 23 2.3.3 Уравнения регрессии. 25 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 27 ПРИЛОЖЕНИЕ А Исходный код для задачи№1 ПРИЛОЖЕНИЕ Б Исходный код для задачи№2 ПРИЛОЖЕНИЕ В Исходный код для задачи№3
ВВЕДЕНИЕ
Математическая статистика - наука, которая занимается анализом случайных данных. Именно эта наука изучает методы (в рамках точных математических моделей), позволяющие отвечать на вопрос, соответствует ли практика, представленная в виде результатов эксперимента, данному гипотетическому представлению о природе явления или нет. При этом имеются в виду не эксперименты, которые позволяют делать однозначные, детерминированные выводы о рассматриваемых явлениях, а эксперименты, результатами которых являются случайные события. С развитием науки задач такого рода становится все больше и больше, поскольку с увеличением точности экспериментов становится все труднее избежать «случайного фактора», связанного с различными помехами и ограниченностью наших измерительных и вычислительных возможностей[1]. В определенном смысле математическая статистика решает задачи, обратные задачам теории вероятностей: она уточняет (выявляет), структуру статистических моделей по результатам проводимых наблюдений. В настоящее время методы математической статистики широко используются в различных технических дисциплинах. Они играют важную роль в экономических исследованиях, сельском хозяйстве, биологии, медицине, физических науках, геологии, психологии и других науках[2].
ЗАДАНИЕ И ИСХОДНЫЕ ДАННЫЕ
1.1 Содержание задания 1. Смоделировать случайную величину 1.1. Построить гистограмму распределения и изобразить ее графически одновременно с теоретической плотностью вероятностей. 1.2. Вычислить выборочное среднее и выборочную дисперсию. 1.3. Найти оценки математического ожидания и дисперсии методом максимального правдоподобия. Указать несмещенную оценку дисперсии. 1.4. Построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности 1.5. Проверить гипотезу о нормальном распределении случайной величины 2. Смоделировать случайную величину 2.1. Построить гистограмму распределения и изобразить ее графически одновременно с теоретической плотностью вероятностей. 2.2. Определить точечные оценки математического ожидания и дисперсии. 2.3. При заданном виде распределения построить оценки входящих в него неизвестных параметров методом моментов. 2.4. Построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности 2.5. Проверить гипотезу о виде распределении случайной величины 3. Смоделировать случайный вектор 3.1. Найти точечные оценки параметров, входящих в распределение. 3.2. Проверить гипотезу о независимости случайных величин 3.3. Найти эмпирические уравнения регрессии Исходные данные Исходные данные к задаче №1 (гр. 628)
Исходные данные к задаче №2
Общее показательное распределение:
Исходные данные: a = 2, b = -4, a = 0.05, g = 0.95, n = 400. Рассчитать аналитически: Найти точечные оценки параметров a и b методом моментов. Исходные данные к задаче №3
ХОД ВЫПОЛНЕНИЯ РАБОТЫ Гистограмма распределения Имеется наблюдаемая случайная величина X, имеющая нормальный закон распределения с заданными параметрами В пакете имеется функция grand(), которая может создавать последовательности случайных чисел из различных распределений. Так вызов этой функции с параметрами grand (1, Требуется построить гистограмму распределения. Сначала найдем выборочные минимум и максимум, используя стандартные функции min, max. Число интервалов группировки определяем с помощью, так называемого, правила Стургерса, согласно которому полагается Полученные результаты представлены в Таблице 1.
Таблица 1 – Интервальный статистический ряд
Здесь
Теперь строим гистограмму вызовом стандартной функции histplot(), полигон частот и график теоретической функции вероятностей (вызов функции plot2d()). Результат представлен на Рисунке 1.
Рисунок 1 – Гистограмма выборки, полигон частот и график теоретической функции вероятностей Доверительные интервалы Пусть наблюдаемая величина Если наблюдаемая случайная величина
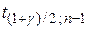 – –  - квантиль распределения Стьюдента - квантиль распределения Стьюдента  с (n —1) степенью свободы, с (n —1) степенью свободы,  – доверительная вероятность, – доверительная вероятность,  - выборочное среднее - выборочное среднее  - выборочная дисперсия. Значение квантиля распределения в нашем случае: - выборочная дисперсия. Значение квантиля распределения в нашем случае:  1,960. Получили следующий интервал для мат. ожидания: 1,960. Получили следующий интервал для мат. ожидания:  Доверительный интервал для дисперсии
После подстановки значений получили: Доверительный интервал для дисперсии
В нашем случае: Если наблюдаемая случайная величина
После подстановки значений получаем: Критерий Пирсона Пусть Критерий согласия 1. По заданному уровню значимости 2. По заданной выборке 3. Если 4. Если В нашем случае рассмотрим отдельно случаи неизвестных и известных параметров распределения. Воспользуемся имеющимися интервалами группировки из пункта 2.1.1, объединив некоторые из них так, чтобы в каждом из интервалов частота группировки была не менее 5. Полученные данные занесем в Таблицу 2. Таблица 2 - Интервальный статистический ряд
Здесь
Найдём значения статистик для случаев известных и неизвестных параметров распределения.
Значения статистик в нашем случае:
Определим пороги для обоих случаев: Таким образом,
Следует сравнить значения соответствующих статистик и порогов и сделать вывод о принятии гипотезы о виде распределения. Очевидно, что значения статистик намного меньше, чем получившиеся пороги, следовательно, можно принять гипотезы о видах распределения как с известными, так и с неизвестными параметрами.
Гистограмма распределения Имеется наблюдаемая случайная величина X, которая имеет общее показательное распределение, с заданными параметрами a и b:
Рассчитаем аналитически числовые характеристики этой случайной величины.
Теперь найдём функцию распределения случайной величины X: Построим графики плотности вероятностей (Рисунок 2) и функции распределения (Рисунок 3).
Рисунок 3 – график функции распределения
Найдём функцию, обратную к функции распределения:
Таким образом, Теперь пусть у нас имеется случайная величина Итак, у нас имеется выборка объёма n Аналогично расчетам из раздела 2.1.1 найдем выборочные максимум, минимум, количество интервалов группировки и ширину интервалов группировки. В нашем случае: Таблица 3 - Статистический интервальный ряд
Подробное описание величин в таблице можно найти в пункте 2.1.1.
Рисунок 4 – гистограмма выборки и график теоретической функции вероятностей Метод моментов У нас имеется выборка объёма n Составим систему уравнений, используя найденные ранее выражения для дисперсии и математического ожидания.
После подсчёта получаем:
Доверительные интервалы Если распределение наблюдаемой случайной величины
где В результате вычислений получаем: Критерий Пирсона Описание используемого метода, необходимых формул и пояснений к ним соответствуют описанию из раздела 2.1.5. Для случая общего показательного распределения составим таблицу для получившихся интервалов группировки: Таблица 4 - Статистический интервальный ряд
Подробное описание величин в таблице можно найти в пункте 2.1.5. Найдём значение статистики: Теперь следует сравнить значение статистики и порога и сделать вывод о принятии гипотезы о законе распределения. Очевидно, что значение статистики меньше чем значение порога, следовательно, можно принять гипотезу о виде распределения. Задача №3. Случайный вектор Гипотеза о независимости В общем случае для проверки гипотезы о независимости случайных величин
где Статистикой критерия для проверки данной гипотезы Таким образом, критерий для проверки гипотезы 1. По заданному уровню значимости 2. По заданной выборке 3. Если 4. Если Для того чтобы воспользоваться критерием χ2, разобьём выборочные значения на одинаковые интервалы группировки, после чего объединим некоторые из них так, чтобы в каждый прямоугольник группировки попало не менее 5 точек. В результате получились следующие одномерные таблицы частот.
Обозначения в этих двух таблицах аналогичны обозначениям в пункте 2.1.1. Построим также двумерную таблицу частот. В ней по вертикали расположим интервалы первой координаты вектора, а по горизонтали – второй.
После этого мы сможем вычислить статистику χ2: Теперь проверим ту же гипотезу с помощью критерия значимости корреляции. Статистика этого критерия: Уравнения регрессии Функцией регрессии Известно, что если случайный вектор
Заменяя в этом уравнении
Аналогично определяется функция регрессии
Геометрически уравнение регрессии представляет собой прямую, около которой группируются значения случайного вектора
Рисунок 5 – график уравнений регрессии ПРИЛОЖЕНИЕ А Исходный код для задачи №1 n=375; a=3,1; D=9,1; g=0,96; alpha=0.01; function p = fx (x) //Функция плотности вероятности p =1/sqrt(2*%pi*D)*exp((-(x -a)^2)/(2*D)); endfunction; X = grand(1, n, 'nor', a, sqrt(D)); //1.1 function [ nu, xb ]= solve1 (X, fx) xmin = min(X); xmax = max(X); N = floor(1 + 3.32 * log10 (n)) + 1; // Кол-во точек на графике delta = (xmax - xmin) / N; // Диапазон ширины xb = zeros(1, N+1); nu =zeros(1, N); ps=zeros(1, N); h=zeros(1, N); p=zeros(1, N); xc=zeros(1, N+2); snu = 0; sps = 0; hmax = 0; xb = xmin + (0:N)'*delta; // Границы интервалов группировки for i = 1: n, for j = 1: N, if (xb (j) <= X (i) & X (i) <= xb (j+1)), nu (j) = nu (j) + 1; // Вычисление частот break; end; end; end; xc(1) = xb (1) - delta / 2; // Escape centre value xc(N+2) = xb (N+1) + delta / 2; // Escape centre value for k = 1: N, snu = snu + nu (k); // Сумма частот ps(k) = nu (k) / n; //Относительные частоты sps = sps+ps(k); //Сумма относительных частот h(k) = ps(k)/delta; //Высоты xc(k+1) = (xb (k)+ b (k+1)) / 2; p(k) = fx (xc(k+1)); //Теоретическая вероятность hmax = max([hmax, h(k)]); end; histplot (N, X, style = 2, rect = [xmin - delta, 0, xmax + delta, hmax + 0.05]); // Построение гистограммы x = [xmin - delta: 0.05: xmax + delta]; plot2d(x, fx (x)); // График теоретической плотности вероятностей plot2d(xc, [0, h, 0], 5); // Полигон частот endfunction; [nu, xb] = solve1 (X, fx); // 1.2. sm = mean (X); //Выборочное среднее disp(abs(sm-a), 'Отклонение мат. ожидания'); sv = mean ((X - sm)^2); //Выборочная дисперсия disp(abs(sv-D), 'Отклонение дисперсии'); // 1.3. csv = n / (n - 1) * sv; //Несмещенная оценка дисперсии disp(abs(csv-D), 'Отклонение'); // 1.4. //границы доверительных интервалов при неизвестной дисперсии и мат. ожидании c=2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.219.241 (0.016 с.) |

 , имеющую нормальный закон распределения с параметрами
, имеющую нормальный закон распределения с параметрами  . На основе выборки объема
. На основе выборки объема  исследовать статистические характеристики случайной величины
исследовать статистические характеристики случайной величины  .
. Пирсона при уровне значимости
Пирсона при уровне значимости  .
. , имеющую заданный непрерывный закон распределения (отличный от нормального) с заданными параметрами. На основе выборки объема
, имеющую заданный непрерывный закон распределения (отличный от нормального) с заданными параметрами. На основе выборки объема  , имеющий двумерный нормальный закон распределения с параметрами
, имеющий двумерный нормальный закон распределения с параметрами  . На основе выборки объема
. На основе выборки объема 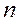





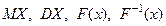 .
.


 . Плотность вероятностей случайной величины X определяется по формуле
. Плотность вероятностей случайной величины X определяется по формуле  . Для того, чтобы смоделировать эту случайную величину на компьютере будем использовать свободный универсальный математический пакет SciLab v.5.3.3.
. Для того, чтобы смоделировать эту случайную величину на компьютере будем использовать свободный универсальный математический пакет SciLab v.5.3.3. ,'nor',
,'nor', 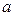 ,
,  )вернёт вектор из n значений копий случайной величины X, т.е. выборку из генеральной совокупности объёма n.
)вернёт вектор из n значений копий случайной величины X, т.е. выборку из генеральной совокупности объёма n. . Ширину интервалов группировки легко определить по формуле
. Ширину интервалов группировки легко определить по формуле 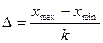 . В нашем случае
. В нашем случае  ,
,  , N = 10,
, N = 10, 





 – границы интервалов группировки;
– границы интервалов группировки; – частоты значений;
– частоты значений;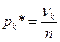 – относительные частоты;
– относительные частоты; – высоты гистограммы;
– высоты гистограммы; – теоретические значения плотности вероятностей в серединах интервалов. Стоит отметить, что
– теоретические значения плотности вероятностей в серединах интервалов. Стоит отметить, что  .
.
 имеет функцию распределения
имеет функцию распределения  , зависящую от неизвестного параметра
, зависящую от неизвестного параметра  . При интервальном оценивании параметра
. При интервальном оценивании параметра  и
и  (
( и
и  - случайные величины!), для которых при заданном
- случайные величины!), для которых при заданном  выполняется соотношение
выполняется соотношение  . В этом случае интервал
. В этом случае интервал  называют
называют  - доверительным интервалом для параметра
- доверительным интервалом для параметра  имеет нормальный закон распределения
имеет нормальный закон распределения  с неизвестным математическим ожиданием
с неизвестным математическим ожиданием  и неизвестной дисперсией
и неизвестной дисперсией  , то доверительный интервал для математического ожидания
, то доверительный интервал для математического ожидания 
 наблюдаемой случайной величины
наблюдаемой случайной величины  имеет вид:
имеет вид:

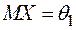 имеет вид:
имеет вид: );
);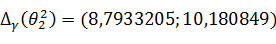
 имеет нормальный закон распределения
имеет нормальный закон распределения  с неизвестным математическим ожиданием
с неизвестным математическим ожиданием  , то доверительный интервал для математического ожидания
, то доверительный интервал для математического ожидания 
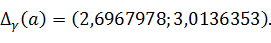
 - выборка объема
- выборка объема 
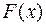 - теоретическая функция распределения, соответствующая гипотезе
- теоретическая функция распределения, соответствующая гипотезе  ). Наиболее распространенным критерием проверки этой гипотезы
). Наиболее распространенным критерием проверки этой гипотезы  находится порог
находится порог  .
. определяется число
определяется число  интервалов группировки так, чтобы
интервалов группировки так, чтобы 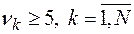 . Вычисляется значение статистики
. Вычисляется значение статистики  .
. , то гипотезу
, то гипотезу  , то гипотезу
, то гипотезу 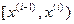


 – границы интервалов группировки;
– границы интервалов группировки;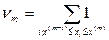 – частоты значений;
– частоты значений; – относительные частоты;
– относительные частоты; – теоретические значения вероятности попадания в интервал; Φ(x) – функция Лапласа;
– теоретические значения вероятности попадания в интервал; Φ(x) – функция Лапласа; – выборочные значения вероятности попадания в интервал.
– выборочные значения вероятности попадания в интервал.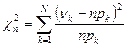 – статистика для случая известных параметров (N – количество интервалов группировки).
– статистика для случая известных параметров (N – количество интервалов группировки). 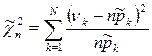 – статистика для случая неизвестных параметров.
– статистика для случая неизвестных параметров.
 .
. – порог. Здесь k – число неизвестных параметров распределения.
– порог. Здесь k – число неизвестных параметров распределения. – порог для случая известных параметров распределения,
– порог для случая известных параметров распределения,  – порог для случая неизвестных параметров распределения. Получаем следующие пороги:
– порог для случая неизвестных параметров распределения. Получаем следующие пороги: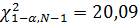 ;
; 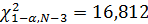 .
.




 Рисунок 2 – график функции плотности вероятностей
Рисунок 2 – график функции плотности вероятностей

 . Тогда можно смоделировать случайную величину X как функцию от случайной величины U, обратную функции распределения случайной величины X:
. Тогда можно смоделировать случайную величину X как функцию от случайной величины U, обратную функции распределения случайной величины X: 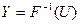 . Пронаблюдав эту величину n раз, мы получим выборку объёма n.
. Пронаблюдав эту величину n раз, мы получим выборку объёма n. , полученная при n наблюдениях за случайной величиной X. Требуется построить гистограмму распределения по этой выборке.
, полученная при n наблюдениях за случайной величиной X. Требуется построить гистограмму распределения по этой выборке. ,
,  , N = 10,
, N = 10,  Полученные данные занесем в Таблицу3.
Полученные данные занесем в Таблицу3. С помощью функции histplot() одновременно строим гистограмму выборки (Рисунок4).
С помощью функции histplot() одновременно строим гистограмму выборки (Рисунок4). с неизвестными параметрами
с неизвестными параметрами  ,
,  > 0. Требуется оценить значение параметров методом моментов, т.е. указать для него точечные оценки
> 0. Требуется оценить значение параметров методом моментов, т.е. указать для него точечные оценки  и
и  .
. ,
, 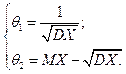
 . Отклонение от реальных значений составляют:
. Отклонение от реальных значений составляют:  .
.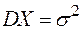 являются:
являются: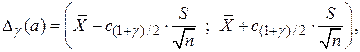

 - выборочная дисперсия;
- выборочная дисперсия;  ;
; 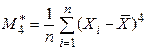 - выборочный центральный момент четвертого порядка[1].
- выборочный центральный момент четвертого порядка[1]. .Очевидно, как найденные ранее выборочные, так и теоретические значения параметра попадают в полученные интервалы.
.Очевидно, как найденные ранее выборочные, так и теоретические значения параметра попадают в полученные интервалы.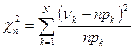 , где N – количество интервалов группировки. Получаем:
, где N – количество интервалов группировки. Получаем:  . Определим порог
. Определим порог  (здесь k=2 – число неизвестных параметров распределения). Таким образом, искомый порог
(здесь k=2 – число неизвестных параметров распределения). Таким образом, искомый порог  =15,086.
=15,086.
 ,
,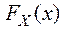 и
и 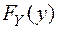 - одномерные функции распределения координат вектора.
- одномерные функции распределения координат вектора. , где
, где  - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции. .
. вычисляется значение статистики
вычисляется значение статистики  .
. , то гипотезу
, то гипотезу  , то гипотезу
, то гипотезу 



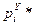
 , где K, L – число получившихся интервалов группировки для X и Y соответственно; ν – двумерная частота группировки; νX, νY – одномерные частоты группировки для X и Y соответственно. В нашем случае получили:
, где K, L – число получившихся интервалов группировки для X и Y соответственно; ν – двумерная частота группировки; νX, νY – одномерные частоты группировки для X и Y соответственно. В нашем случае получили:  . Зададимся порогом:
. Зададимся порогом: 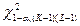 , который представляет собой (1-α)-квантиль распределения
, который представляет собой (1-α)-квантиль распределения  . В нашем случае
. В нашем случае  . Статистика превышает порог, значит, гипотезу о независимости величин X и Y следует отвергнуть.
. Статистика превышает порог, значит, гипотезу о независимости величин X и Y следует отвергнуть. , где
, где  – выборочный коэффициент корреляции. В нашем случае T = - 8.9744155. Порогом данной статистики является
– выборочный коэффициент корреляции. В нашем случае T = - 8.9744155. Порогом данной статистики является  , т.е.
, т.е. 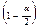 -квантиль распределения Стьюдента с числом степеней свободы (n-2). В нашем случае
-квантиль распределения Стьюдента с числом степеней свободы (n-2). В нашем случае  . Так как область для проверки критерия определяется в виде
. Так как область для проверки критерия определяется в виде  , гипотезу о независимости случайных величин X и Y следует опровергнуть.
, гипотезу о независимости случайных величин X и Y следует опровергнуть. случайной величины
случайной величины  . Эта функция наилучшим (в среднеквадратическом смысле) образом описывает зависимость случайной величины
. Эта функция наилучшим (в среднеквадратическом смысле) образом описывает зависимость случайной величины  , то функция регрессии случайной величины
, то функция регрессии случайной величины  .
. на их точечные оценки
на их точечные оценки  соответственно, получаем эмпирическое уравнение регрессии случайной величины
соответственно, получаем эмпирическое уравнение регрессии случайной величины 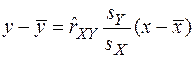 .
. случайной величины
случайной величины 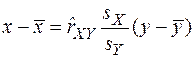 .
.



