
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача №2. Показательный закон распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гистограмма распределения Имеется наблюдаемая случайная величина X, которая имеет общее показательное распределение, с заданными параметрами a и b:
Рассчитаем аналитически числовые характеристики этой случайной величины.
Теперь найдём функцию распределения случайной величины X: Построим графики плотности вероятностей (Рисунок 2) и функции распределения (Рисунок 3).
Рисунок 3 – график функции распределения
Найдём функцию, обратную к функции распределения:
Таким образом, Теперь пусть у нас имеется случайная величина Итак, у нас имеется выборка объёма n Аналогично расчетам из раздела 2.1.1 найдем выборочные максимум, минимум, количество интервалов группировки и ширину интервалов группировки. В нашем случае: Таблица 3 - Статистический интервальный ряд
Подробное описание величин в таблице можно найти в пункте 2.1.1.
Рисунок 4 – гистограмма выборки и график теоретической функции вероятностей Выборочные числовые характеристики Описание используемого метода, необходимых формул и пояснений к ним соответствуют описанию из раздела 2.1.1. Для случая общего показательного распределения:
Отклонения от теоретических характеристик составляют:
Метод моментов У нас имеется выборка объёма n Составим систему уравнений, используя найденные ранее выражения для дисперсии и математического ожидания.
После подсчёта получаем: Доверительные интервалы Если распределение наблюдаемой случайной величины
где В результате вычислений получаем: Критерий Пирсона Описание используемого метода, необходимых формул и пояснений к ним соответствуют описанию из раздела 2.1.5. Для случая общего показательного распределения составим таблицу для получившихся интервалов группировки: Таблица 4 - Статистический интервальный ряд
Подробное описание величин в таблице можно найти в пункте 2.1.5. Найдём значение статистики: Теперь следует сравнить значение статистики и порога и сделать вывод о принятии гипотезы о законе распределения. Очевидно, что значение статистики меньше чем значение порога, следовательно, можно принять гипотезу о виде распределения. Задача №3. Случайный вектор
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 624; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.151 (0.008 с.) |






 Рисунок 2 – график функции плотности вероятностей
Рисунок 2 – график функции плотности вероятностей

 . Тогда можно смоделировать случайную величину X как функцию от случайной величины U, обратную функции распределения случайной величины X:
. Тогда можно смоделировать случайную величину X как функцию от случайной величины U, обратную функции распределения случайной величины X: 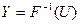 . Пронаблюдав эту величину n раз, мы получим выборку объёма n.
. Пронаблюдав эту величину n раз, мы получим выборку объёма n. , полученная при n наблюдениях за случайной величиной X. Требуется построить гистограмму распределения по этой выборке.
, полученная при n наблюдениях за случайной величиной X. Требуется построить гистограмму распределения по этой выборке. ,
,  , N = 10,
, N = 10,  Полученные данные занесем в Таблицу3.
Полученные данные занесем в Таблицу3.



 С помощью функции histplot() одновременно строим гистограмму выборки (Рисунок4).
С помощью функции histplot() одновременно строим гистограмму выборки (Рисунок4).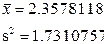

 с неизвестными параметрами
с неизвестными параметрами  ,
,  > 0. Требуется оценить значение параметров методом моментов, т.е. указать для него точечные оценки
> 0. Требуется оценить значение параметров методом моментов, т.е. указать для него точечные оценки  и
и  .
. ,
, 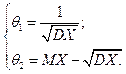
 . Отклонение от реальных значений составляют:
. Отклонение от реальных значений составляют:  .
. произвольное (не обязательно нормальное), то, используя асимптотическую нормальность выборочных моментов, можно показать, что при больших объемах выборки приближенными (асимптотическими) доверительными интервалами для математического ожидания
произвольное (не обязательно нормальное), то, используя асимптотическую нормальность выборочных моментов, можно показать, что при больших объемах выборки приближенными (асимптотическими) доверительными интервалами для математического ожидания  и дисперсии
и дисперсии 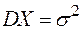 являются:
являются: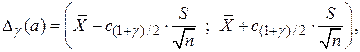

 - выборочное среднее;
- выборочное среднее;  - выборочная дисперсия;
- выборочная дисперсия;  ;
; 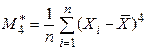 - выборочный центральный момент четвертого порядка[1].
- выборочный центральный момент четвертого порядка[1]. .Очевидно, как найденные ранее выборочные, так и теоретические значения параметра попадают в полученные интервалы.
.Очевидно, как найденные ранее выборочные, так и теоретические значения параметра попадают в полученные интервалы.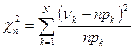 , где N – количество интервалов группировки. Получаем:
, где N – количество интервалов группировки. Получаем:  . Определим порог
. Определим порог  (здесь k=2 – число неизвестных параметров распределения). Таким образом, искомый порог
(здесь k=2 – число неизвестных параметров распределения). Таким образом, искомый порог  =15,086.
=15,086.


