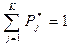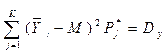Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет числовых характеристик закона распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Контролируемого параметра
Случайная величина будет полностью описана с вероятностной точки зрения, если определить закон ее распределения, под которым понимается определенное соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Контролируемый параметр изнашиваемой детали является непрерывной случайной величиной, закон распределения которой может быть представлен плотностью распределения. Среднее значение контролируемого параметра Y в i- м сечении:
Среднеквадратическое отклонение контролируемого параметра:
где Ni – число значений контролируемого параметра на замер с данным номером i (в i -ом сечении). Все значения контролируемого параметра, которые лежат за пределами интервала [ mi – 3×s i; mi + 3×s i ], исключаются из дальнейшего рассмотрения. Для построения плотности распределения контролируемого параметра область его определения делится на K интервалов и подсчитываются величины D n*j – число значений контролируемого параметра, попавших в j- ый интервал, где j = 1, 2,..., K. Число интервалов разбиения можно определить используя правило Страджесса: K = 1 + 3,3 lg n, (3)
где n – объем выборки статистической совокупности (для j- го сечения). Согласно этому правилу, при объеме статистической совокупности от n = 100 до n = 1000 рекомендуемое число интервалов находится в диапазоне 8–11. Поэтому при определении закона распределения контролируемого параметра число интервалов удобнее принять равным 10, так как на практике число замеров контролируемых параметров изнашиваемых деталей ЭПС находится обычно в пределах n = 100–1000. Поскольку ширина интервала возможных значений нормально распределенной случайной величины равна 6σ y, то ширина j -го интервала группирования принимается равной 0,6σ y. Частота попаданий контролируемого параметра в j -й интервал определена по формуле:
После определения числа попаданий реализаций случайной величины в каждый из интервалов группирования строится гистограмма, для чего по оси абсцисс откладываются интервалы группирования и на каждом из них строится прямоугольник, площадь которого равна частоте данного интервала Высота прямоугольника определяется как:
Исходя из характера гистограммы выбирают закон распределения, с помощью которого выравнивается выявленный статистический ряд. Затем проверяют, согласуются ли полученные данные с гипотезой о том, что случайная величина имеет выбранный закон распределения, заданный плотностью распределения f (y). Мерой согласования теоретического и статистического распределения служит критерий Пирсона (критерий c2), который позволяет определить вероятность того, что за счет случайных причин мера расхождения теоретического и статистического распределения будет больше, чем фактически наблюдаемая. Расчетное значение критерия Пирсона определяется как:
где D nj – теоретическое число значений случайной величины в j- м интервале.
где Pj – теоретическая вероятность попадания случайной величины в j -ый интервал. Теоретическая вероятность попадания случайной величины в j- ый интервал определяется зависимостью:
где yj – 1 – левая граница j- го интервала; yj – правая граница j- го интервала; Zj – значение функции распределения в точке yj; Zj – 1 – то же в точке yj – 1. Чем больше разность (D n*j –D nj), тем меньше полученное статистическое распределение соответствует предлагаемому теоретическому распределению. После определения меры расхождения c2 вычисляется число степеней свободы: r = K – S, (9)
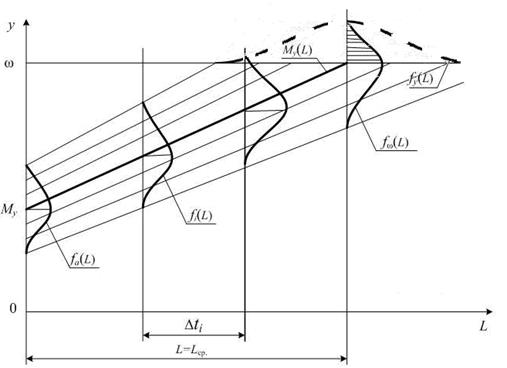
где K – число разрядок гистограммы; S – число связей, накладываемых на частоты Вероятность того, что деталь ЭПС при наработке Li находится в неработоспособном состоянии, соответствует заштрихованной площади кривой распределения fi (y) над границей w (рис. 4). Приращение этой площади за период наработки (Li, Li+ 1) пропорционально вероятности отказа детали ЭПС за этот период. Таким образом происходит формирование закона распределения f (L).
Рис. 4. Схема формирования постепенных отказов связей
Для гистограммы найдена адекватная математическая модель закона распределения износа детали (узла) электроподвижного состава. Выборки контролируемых параметров изнашиваемых узлов ЭПС хорошо описываются нормальным законом, плотность распределения которого:
где Му – математическое ожидание контролируемого параметра; s y – среднеквадратическое отклонение контролируемого параметра; y – текущее значение контролируемого параметра. На случайную величину, подчиненную нормальному закону распределения, накладываются следующие связи:
Таким образом, S = 3 и число степеней свободы распределения будет r = K – 3, т.е. r = 7. Расчеты нормального закона распределения и его числовых характеристик производятся по специальной программе на ПЭВМ. Результаты расчетов числовых характеристик My и s y нормального закона распределения контролируемого параметра при всех значениях пробегов Li представляются в виде таблицы (табл. 1), которая ставит в соответствие каждому пробегу числовые характеристики Myi и s yi, т. е. задает эмпирические зависимости M*y (L) и s *y (L) Для того чтобы осуществить прогнозирование процесса изнашивания деталей и определить их технический ресурс, необходимо построить аналитические зависимости числовых характеристик среднего значения My и среднеквадратического отклонения s y от пробега. Эта задача решается методами регрессионного анализа.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 809; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.118 (0.008 с.) |

 . (1)
. (1) (2)
(2) (4)
(4) .
.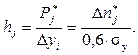 (5)
(5)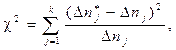 (6)
(6) , (7)
, (7)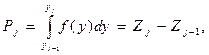 (8)
(8) .
.
 (10)
(10)