Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение различий законов распределенияСодержание книги
Поиск на нашем сайте
Число классов в распределениях до и после объединения равно
Число степеней свободы (первичное и вторичное)
По таблицам [1] находим стандартное значение критерия Таким образом, при любой ответственности испытаний Если проверка дает отрицательный результат, необходимо принять другой вид теоретического закона и повторить процедуру проверки. Если проверки по всем приведенным в настоящих методических указаниях законам (нормальному, Вейбулла и экспоненциальному) не дали положительных результатов, следует на этом ограничиться и сделать заключение о том, что эмпирическое распределение не соответствует ни одному из предложенных теоретических законов. После этого следует вычислить границы доверительного интервала для математического ожидания ресурса, поскольку его истинное значение заменяем его приближенным значением (средним арифметическим), полученным из опыта (наблюдения).
4. Определение доверительного интервала для математического ожидания случайной величины В рассмотренном способе оценки числовых характеристик случайных величин неизвестный параметр определялся одним числом. Такая оценка называется точечной. При оценке надежности машин и оборудования часто требуется не только найти для заданного параметра числовое значение, но и оценить его точность и достоверность. Это особенно актуально при небольшом объеме выборки. Необходимо определить, к каким ошибкам может привести замена искомого параметра (например, математического ожидания) его точечной оценкой (средним арифметическим) и с какой степенью уверенности можно ожидать, что ошибки не выйдут за заданные пределы. В математической статистике для этой цели используют так называемые доверительные интервалы и вероятности. Пусть для параметра
Это равенство означает, что с вероятностью
Интервал Рассмотрим зависимости, используемые при построении доверительных интервалов для параметров случайной величины, распределенной по нормальному закону. Для математического ожидания границы доверительного интервала определяют по формуле
где П р и м е р. Определить доверительные интервалы для математического ожидания ресурса по результатам испытаний бензомоторных пил МП-5 “Урал”, если объем выборки
При Доверительный интервал для математического ожидания ресурса согласно формуле (19)
Таким образом, точное значение ресурса бензомоторных пил МП-5 “Урал“ с вероятностью 0,9 находится в пределах от 228,13 до 495,87 мото-ч. Если закон распределения случайной величины неизвестен, границы доверительного интервала можно определять по формулам для нормального закона.
З А Д А Ч И
З а д а ч а 1 Рассчитать ВБР сложной системы, имеющей структурную формулу и значение ВБР элементов в соответствии с вариантом задания. Изобразить структурную схему этой системы. Исходные данные задачи приведены в табл. 8. Т а б л и ц а 8 Исходные данные к задаче 1
Под сложной системой понимается объект (узел, агрегат, машина), предназначенный для выполнения определенных функций, и который может быть расчленен на элементы (составные части). Элементом является составная часть системы, неделимая на части (с точки зрения надежности), которая характеризуется самостоятельными входными и выходными параметрами и находится во взаимосвязи с другими элементами системы.
Большинство машин и оборудования, с которыми мы имеем дело, являются сложными системами. В зависимости от способа соединения элементов между собой различают три вида связей: последовательное, параллельное и смешанное (последовательно-параллельное). При последовательном соединении элементов (рис. 5) отказ любого элемента приводит к отказу системы. Вероятность безотказной работы такой системы равна произведению вероятностей безотказной работы составляющих ее элементов:
где
Рис. 5. Структурная схема системы при последовательном соединении элементов.
Если все элементы системы равнонадежны, т.е.
П р и м е р 1. Если
Такая связь не обеспечивает высокой надежности системы. Чем сложнее система (чем больше в ней элементов), тем ниже ее ВБР, так как каждый сомножитель в формуле (20) меньше единицы. При этом надежность системы лимитирует элемент, имеющий самую низкую ВБР. Поэтому для повышения надежности системы при такой связи элементов используют резервирование (смотри ниже). Последовательное соединение имеет место практически во всех типах приводов машин (станков, стендов, автомобилей, тракторов, грузоподъемных кранов и т.п.), вследствие того, что при этом достигаются наименьшие габариты, масса, стоимость системы и наиболее простая ее конструкция. При параллельном соединении элементов в системе (рис. 6) ее отказ возможен только после отказа всех элементов. ВБР системы в этом случае определяется по формуле
где Если все элементы системы равнонадежны, т.е.
Рис. 6. Структурная схема системы при параллельном соединении элементов
П р и м е р 2. Если
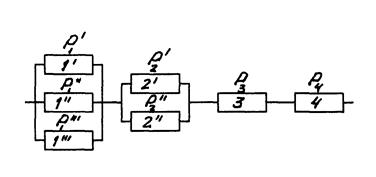
Такая связь элементов в системе обеспечивает ей высокую надежность, но при этом существенно возрастают габариты, масса и стоимость системы. Поэтому такие системы применяются сравнительно редко: в тех случаях когда требования высокой надежности являются превалирующими (например, в авиации, космонавтике, крупных энергетических установках, АСУП и т.п.). В обычных машинах (автомобилях, тракторах, кранах, стендах) и установках такие системы используются редко. В качестве примера можно (условно) назвать наличие нескольких тормозных систем и запасных колес на автомобилях, индивидуальных ЗИПов на машинах, запасных частей на складе и т.п. Смешанным называют такое соединение, когда в системе имеются участки как с параллельной, так и с последовательной связью элементов (рис. 7).
Рис. 7. Структурная схема системы при смешанном соединении элементов
Чаще всего такие системы образуются из систем с последовательной связью, где наиболее слабые элементы резервируют путем параллельного подсоединения к ним дополнительных элементов, что позволяет повысит надежность системы в целом. ВБР такой системы рассчитывают в два этапа: сначала определяют ВБР участков с параллельным соединением по формуле (22), а затем - ВБР всей системы, считая ее состоящей из последовательно соединенных элементов. Таким образом, смешанное соединение элементов заменяется последовательным, как показано на рис. 5, где элементы 1 и 2 заменяют собой участки соответственно
П р и м е р 3. Определить ВБР системы, структурная схема которой показана на рис. 7. Такая схема могла бы получиться в результате резервирования наименее надежных элементов- первого и второго. ВБР системы без резервирования была бы равна
т.е. очень низкой.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.009 с.) |




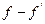

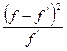


 : 9,5; 13,3; 18,5 при
: 9,5; 13,3; 18,5 при  соответственно 0,95; 0,99; 0,999.
соответственно 0,95; 0,99; 0,999. , то есть различия недостоверны. Можно считать, что эмпирическое распределение не противоречит распределению Вейбулла.
, то есть различия недостоверны. Можно считать, что эмпирическое распределение не противоречит распределению Вейбулла. (например,математического ожидания) получена по результатам выборочного обследования точечная оценка этого параметра
(например,математического ожидания) получена по результатам выборочного обследования точечная оценка этого параметра  . Требуется определить ошибку замены параметра
. Требуется определить ошибку замены параметра  и определим такое значение ошибки
и определим такое значение ошибки  , для которого
, для которого .
.
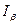 называется доверительным, а
называется доверительным, а  (19)
(19) коэффициент распределения Стьюдента, определяемый по таблицам [1] в зависимости от доверительной вероятности
коэффициент распределения Стьюдента, определяемый по таблицам [1] в зависимости от доверительной вероятности 
 , ресурс распределен по нормальному закону с параметрами
, ресурс распределен по нормальному закону с параметрами  ;
;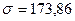 ;
; 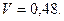
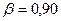 и
и  коэффициент Стьюдента
коэффициент Стьюдента  [1].
[1].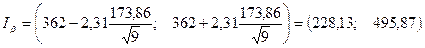


 (20)
(20) - ВБР системы;
- ВБР системы; - ВБР
- ВБР  -го элемента;
-го элемента; - количество последовательно соединенных элементов;
- количество последовательно соединенных элементов; - знак произведения.
- знак произведения.
 , то
, то (21)
(21) , то
, то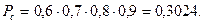
 (22)
(22) - количество параллельно соединенных элементов.
- количество параллельно соединенных элементов. (23)
(23)
 то
то
 и
и  на рис. 7.
на рис. 7.