Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значение классового промежутка вычисляют по формулеСодержание книги
Поиск на нашем сайте
УДК 630.36 К у з н е ц о в Н. И., А б а к у м о в Н. В. Надежность машин и оборудования: Методические указания и задания на выполнение расчетных работ и задач. - Архангельск: Изд-во АГТУ, 2001.-37 с. Подготовлены кафедрой эксплуатации автомобилей и машин лесного комплекса АГТУ. Приведены задания и методические указания для выполнения 2-х расчетных работ и 11 задач. Предназначены для студентов механического и заочного факультетов специальностей 1704 “Машины и оборудование лесного комплекса” и 1502 “Автомобили и автомобильное хозяйство”. Ил. 9. Табл. 12. Библиогр. 7 назв.
Р А С Ч Е Т Н А Я Р А Б О Т А № 1 ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ ПЕРИОДИЧНОСТИ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ ПО УРОВНЮ МИНИМАЛЬНЫХ УДЕЛЬНЫХ ЗАТРАТ НА ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ МАШИН
Сущность метода Удельными называют затраты, отнесенные к единице наработки. Применительно к автомобилям - это 1000 км пробега, к тракторам и машинам на их базе - 100 мото-ч работы, стационарному оборудованию - 100 маш.-ч. Оптимальной является такая периодичность технического обслуживания (ТО), при которой (по данному методу) удельные суммарные затраты на ТО и ремонты будут минимальными. Сущность метода проиллюстрирована на рис. 1.
Рис. 1. Определение оптимальной периодичности тех- нического обслуживания Если ТО проводить реже (увеличивать периодичность), то удельные затраты на его выполнение будут уменьшаться (кривая
Задание и указания к выполнению По исходным данным, приведенным в прил. 1, необходимо: а) определить оптимальную периодичность ТО; б) построить графики зависимости от наработки: вероятности безотказной работы (ВБР), вероятности отказа, удельных затрат (на ТО, ремонты и суммарных): в) рассчитать значения коэффициента готовности и построить график его зависимости от наработки. В исходных данных приняты следующие условные обозначения:
Для выполнения задания необходимо определить: а) среднюю наработку на отказ,
где
б) среднее квадратическое отклонение наработки на отказ, км,
в) коэффициент вариации,%,
г) плотность вероятности безотказной работы (при нормальном законе распределения)
д) вероятность безотказной работы
е) вероятность отказа
ж) удельные затраты, руб/км: на техническое обслуживание
где на ремонты
суммарные
з) минимальные суммарные удельные затраты и соответствующая им оптимальная периодичность ТО определяются минимумом кривой и) коэффициент готовности
Указанные расчеты выполняются с помощью компьютера. При этом рекомендуется придерживаться следующей последовательности работ: взятые из прил. 1 исходные данные следует ввести в компьютер (C:\PROGRAM\LAB\nar.exe). После просмотра результатов расчета их необходимо вывести на печать (print.bat); дополнительно к данным компьютера необходимо вычислить коэффициент вариации по формуле (3) и пересчитать значения коэффициента готовности по формуле (10).
Р А С Ч Е Т Н А Я Р А Б О Т А № 2 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ И ПОСТРОЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
Общие положения Большинство показателей надежности (вероятность безотказной работы, наработка на отказ, ресурс, срок службы и др.) являются статистическими, т.е. случайными, подверженными значительному разбросу. Поэтому для их оценки применяются методы теории вероятностей и математической статистики. Законом распределения случайной величины называют всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (частотами). Эмпирические распределения могут иметь любую (произвольную) форму, которую трудно описать какой-либо аналитической зависимостью. Теоретические же законы имеют конкретное математическое выражение и достаточно хорошо обоснованы. Поэтому задача исследователя состоит в том, чтобы подобрать к полученному из опытного материала эмпирическому распределению одно из известных теоретических распределений. При оценке надежности машин наиболее часто встречаются распределения вида нормального (Гаусса), логарифмически-нормального, Вейбулла, экспоненциального, и др.
Если вид закона распределения предварительно известен, то расчет его параметров и построение теоретического закона можно разделить на следующие этапы: представление статистических данных в виде вариационного (статистического) ряда или гистограммы; определение параметров закона распределения; проверка согласия теоретического и эмпирического распределений по критериям согласия Пирсона построение графика теоретической кривой распределения, если это необходимо. Если же вид закона распределения предварительно не установлен, то это можно сделать после построения эмпирического закона по его внешнему виду или, исходя из физической сущности изучаемого явления.
Задание
По данным, приведенным в прил. 2 (они представляют собой ресурсы автомобилей или их агрегатов до капитального ремонта в тысячах километров пробега), необходимо: - определить среднее арифметическое значение ресурса автомобиля до капитального ремонта; - рассчитать среднее квадратическое отклонение ресурса; - определить коэффициент вариации ресурса; - построить эмпирический закон распределения ресурса; - подобрать теоретический закон; - проверить согласие теоретического и эмпирического законов распределений; - определить доверительный интервал для математического ожидания ресурса.
Указания к выполнению 1. Расчет параметров экспериментального распределения Для большей наглядности и компактности статистические данные преобразуют в статистический ряд, который строится в следующем порядке. Определяют размах выборки, то есть разницу между максимальным и минимальным значениями
затем размах выборки Число классов зависит от числа наблюдений.
где Т а б л и ц а 4 Рис. 3. Выравнивание статистического ряда по закону распределения Вейбулла
Э к с п о н е н ц и а л ь н ы й з а к о н. Теоретические частоты для экспоненциального закона распределения определяют по формуле
где
П р и м е р. Проведем выравнивание по экспоненциальному закону эмпирического распределения наработки на отказ бензомоторных пил МП-5 “Урал” ( Выравнивание эмпирического распределения наработки на отказ приведено в табл. 5 и на рис. 4. Т а б л и ц а 5 Распределения
Продолжение прил. 1
Рис. 4. Выравнивание статистического ряда по экспоненциальному закону распределения
3. Оценка различий эмпирического и теоретического распределений Методика оценки различий эмпирического и теоретического распределений для различных законов распределения одна и та же. Для проверки согласованности теоретического и эмпирического распределений чаще всего используют критерий
где
Первичное
где Крайние классы с частотой Т а б л и ц а 6 Исходные данные к задаче 2
Преимущества параллельного соединения элементов позволяют использовать его для повышения надежности сложных систем путем резервирования. Резервированием называют способ повышения надежности систем путем введения частей, являющихся избыточными по отношению к минимальной функциональной структуре системы. Наиболее часто применяются два основных способа резервирования: раздельное и общее. При раздельном резервировании (рис. 8) имеется возможность включать резервный элемент всякий раз, когда отказывает основной. ВБР системы в этом случае определяется по формуле
где j=m – количество параллельно подсоединенных элементов. УДК 630.36 К у з н е ц о в Н. И., А б а к у м о в Н. В. Надежность машин и оборудования: Методические указания и задания на выполнение расчетных работ и задач. - Архангельск: Изд-во АГТУ, 2001.-37 с. Подготовлены кафедрой эксплуатации автомобилей и машин лесного комплекса АГТУ. Приведены задания и методические указания для выполнения 2-х расчетных работ и 11 задач.
Предназначены для студентов механического и заочного факультетов специальностей 1704 “Машины и оборудование лесного комплекса” и 1502 “Автомобили и автомобильное хозяйство”. Ил. 9. Табл. 12. Библиогр. 7 назв.
Р А С Ч Е Т Н А Я Р А Б О Т А № 1 ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ ПЕРИОДИЧНОСТИ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ ПО УРОВНЮ МИНИМАЛЬНЫХ УДЕЛЬНЫХ ЗАТРАТ НА ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ МАШИН
Сущность метода Удельными называют затраты, отнесенные к единице наработки. Применительно к автомобилям - это 1000 км пробега, к тракторам и машинам на их базе - 100 мото-ч работы, стационарному оборудованию - 100 маш.-ч. Оптимальной является такая периодичность технического обслуживания (ТО), при которой (по данному методу) удельные суммарные затраты на ТО и ремонты будут минимальными. Сущность метода проиллюстрирована на рис. 1.
Рис. 1. Определение оптимальной периодичности тех- нического обслуживания Если ТО проводить реже (увеличивать периодичность), то удельные затраты на его выполнение будут уменьшаться (кривая
Задание и указания к выполнению По исходным данным, приведенным в прил. 1, необходимо: а) определить оптимальную периодичность ТО; б) построить графики зависимости от наработки: вероятности безотказной работы (ВБР), вероятности отказа, удельных затрат (на ТО, ремонты и суммарных): в) рассчитать значения коэффициента готовности и построить график его зависимости от наработки. В исходных данных приняты следующие условные обозначения:
Для выполнения задания необходимо определить: а) среднюю наработку на отказ,
где
б) среднее квадратическое отклонение наработки на отказ, км,
в) коэффициент вариации,%,
г) плотность вероятности безотказной работы (при нормальном законе распределения)
д) вероятность безотказной работы
е) вероятность отказа
ж) удельные затраты, руб/км: на техническое обслуживание
где на ремонты
суммарные
з) минимальные суммарные удельные затраты и соответствующая им оптимальная периодичность ТО определяются минимумом кривой и) коэффициент готовности
Указанные расчеты выполняются с помощью компьютера. При этом рекомендуется придерживаться следующей последовательности работ:
взятые из прил. 1 исходные данные следует ввести в компьютер (C:\PROGRAM\LAB\nar.exe). После просмотра результатов расчета их необходимо вывести на печать (print.bat); дополнительно к данным компьютера необходимо вычислить коэффициент вариации по формуле (3) и пересчитать значения коэффициента готовности по формуле (10).
Р А С Ч Е Т Н А Я Р А Б О Т А № 2 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ И ПОСТРОЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
Общие положения Большинство показателей надежности (вероятность безотказной работы, наработка на отказ, ресурс, срок службы и др.) являются статистическими, т.е. случайными, подверженными значительному разбросу. Поэтому для их оценки применяются методы теории вероятностей и математической статистики. Законом распределения случайной величины называют всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (частотами). Эмпирические распределения могут иметь любую (произвольную) форму, которую трудно описать какой-либо аналитической зависимостью. Теоретические же законы имеют конкретное математическое выражение и достаточно хорошо обоснованы. Поэтому задача исследователя состоит в том, чтобы подобрать к полученному из опытного материала эмпирическому распределению одно из известных теоретических распределений. При оценке надежности машин наиболее часто встречаются распределения вида нормального (Гаусса), логарифмически-нормального, Вейбулла, экспоненциального, и др. Если вид закона распределения предварительно известен, то расчет его параметров и построение теоретического закона можно разделить на следующие этапы: представление статистических данных в виде вариационного (статистического) ряда или гистограммы; определение параметров закона распределения; проверка согласия теоретического и эмпирического распределений по критериям согласия Пирсона построение графика теоретической кривой распределения, если это необходимо. Если же вид закона распределения предварительно не установлен, то это можно сделать после построения эмпирического закона по его внешнему виду или, исходя из физической сущности изучаемого явления.
Задание
По данным, приведенным в прил. 2 (они представляют собой ресурсы автомобилей или их агрегатов до капитального ремонта в тысячах километров пробега), необходимо: - определить среднее арифметическое значение ресурса автомобиля до капитального ремонта; - рассчитать среднее квадратическое отклонение ресурса; - определить коэффициент вариации ресурса; - построить эмпирический закон распределения ресурса; - подобрать теоретический закон; - проверить согласие теоретического и эмпирического законов распределений; - определить доверительный интервал для математического ожидания ресурса.
Указания к выполнению 1. Расчет параметров экспериментального распределения Для большей наглядности и компактности статистические данные преобразуют в статистический ряд, который строится в следующем порядке. Определяют размах выборки, то есть разницу между максимальным и минимальным значениями
затем размах выборки Число классов зависит от числа наблюдений.
где Значение классового промежутка вычисляют по формуле
После этого определяют середины классов и их границы и подсчитывают частоты, то есть число значений случайной величины Существует несколько способов вычисления параметров распределения. Рассмотрим на примере более подробно порядок определения среднего арифметического значения и среднего квадратического отклонения по способу произведений [1]. С о с т а в л е н и е с т а т и с т и ч е с к о г о р я д а. Составление статистического ряда и все последующие вычисления произведем на примере, исходные данные которого представляют собой наработки на отказ в мото-ч гидросистемы трактора ТДТ-55А: 413 450 419 412 427 435 404 430 421 399 432 420 416 407 407 428 417 398 424 420 414 410 409 416 430 403 426 407 400 423 423 434 402 431 410 405 436 405 424 405 433 395 433 420 439 398 437 422 394 416 414 386 428 441 397 417 418 414 429 417 401 424 411 426 380 419 406 419 429 406 425 391 432 409 418 418 386 421 415 417 413 413 444 392 411 428 394 431 411 422 424 434 408 443 407 421 422 410 423 409 Число классов статистического ряда определяем по формуле (11)
Принимаем Размах выборки для нашего ряда
Значение классового промежутка находим по формуле (12):
Для удобства вычислений принимаем Середина классов Начало
где Например, для класса с серединой
Пример составления статистического ряда приведен в табл. 1.
Т а б л и ц а 1 Составление статистического ряда
В ы ч и с л е н и е с р е д н е г о а р и ф м е т и ч е с к о г о з н а ч е – н и я и с р е д н е г о к в а д р а т и ч е с к о г о о т к л о н е н и я. Среднее арифметическое значение случайной величины способом произведений вычисляем по формуле
где
классовых промежутках,
Среднее квадратическое отклонение определяем по формуле
где
В табл. 2 приведены вспомогательные вычисления для определения Т а б л и ц а 2 Вспомогательные вычисления для определения
Расчеты, произведенные по вышеприведенным формулам, дают следующие результаты: После вычисления параметров распределения определяют вид закона распределения случайной величины.
2. Определение вида закона распределения случайной величины Закон распределения случайной величины определяют в следующей последовательности: выравнивают эмпирический ряд одним из теоретических распределений; производят оценку различий эмпирического и теоретического распределений по критериям Рассмотрим выравнивание эмпирических статистических кривых при разных законах распределения случайной величины и проверку согласованности эмпирического и теоретического распределений.
Н о р м а л ь н ы й з а к о н. Теоретические частоты при нормальном законе распределения случайной величины определяют по формуле
где
П р и м е р. Выполним выравнивание статистического ряда, приведенного в табл. 1, по нормальному закону распределения с параметрами Выравнивание приведено в табл. 3 и на рис. 2.
Т а б л и ц а 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.66.242 (0.008 с.) |


 ). Но при этом будет увеличиваться количество отказов, а следовательно, и удельные затраты на устранение их последствий - (ремонт), (кривая
). Но при этом будет увеличиваться количество отказов, а следовательно, и удельные затраты на устранение их последствий - (ремонт), (кривая  ). Графическое сложение этих кривых дает зависимость суммарных удельных затрат на ТО и ремонты от периодичности ТО (кривая
). Графическое сложение этих кривых дает зависимость суммарных удельных затрат на ТО и ремонты от периодичности ТО (кривая  ). Минимум этой кривой и определяет оптимальную периодичность ТО.
). Минимум этой кривой и определяет оптимальную периодичность ТО. 1…
1…  – стоимость одного ТО, руб.;
– стоимость одного ТО, руб.; – стоимость устранения последствий одного отказа (стоимость одного ремонта), руб.;
– стоимость устранения последствий одного отказа (стоимость одного ремонта), руб.; – продолжительность выполнения одного ТО, дней;
– продолжительность выполнения одного ТО, дней; – продолжительность устранения последствий одного отказа, дней;
– продолжительность устранения последствий одного отказа, дней;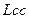 – среднесуточный пробег (наработка), км;
– среднесуточный пробег (наработка), км; – требуемая вероятность безотказной работы;
– требуемая вероятность безотказной работы; – интервал пробега (наработки), км
– интервал пробега (наработки), км (1)
(1) наработка на каждый отказ, км;
наработка на каждый отказ, км; - количество отказов;
- количество отказов; ; (2)
; (2)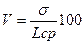 ; (3)
; (3) : (4)
: (4) ; (5)
; (5) ; (6)
; (6)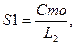 (7)
(7)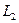 - периодичность ТО, км;
- периодичность ТО, км; (8)
(8) 
 ; (9)
; (9) ;
; . (10)
. (10)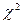 или Колмогорова
или Колмогорова  ;
;
 делят на разряды (классы, интервалы) и определяют величину классового промежутка.
делят на разряды (классы, интервалы) и определяют величину классового промежутка. (11)
(11) (17)
(17)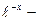 экспоненциальная функция, значения которой табулированы [1];
экспоненциальная функция, значения которой табулированы [1];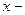 условные отклонения середин классов,
условные отклонения середин классов,
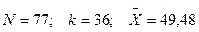 мото-ч).
мото-ч).

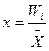




 Пирсона, величину которого рассчитывают по формуле
Пирсона, величину которого рассчитывают по формуле (18)
(18) стандартные значения критерия, его значения находят по специальным таблицам в зависимости от числа степеней свободы
стандартные значения критерия, его значения находят по специальным таблицам в зависимости от числа степеней свободы 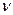 [1];
[1]; эмпирические и теоретические частоты классов
эмпирические и теоретические частоты классов 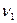 и вторичное
и вторичное  числа степеней свободы определяют по следующим формулам:
числа степеней свободы определяют по следующим формулам:

 числа классов до и после объединения классов с малыми теоретическими частотами.
числа классов до и после объединения классов с малыми теоретическими частотами.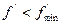 объединяют с соседними классами (
объединяют с соседними классами ( минимально допустимая теоретическая частота крайних классов в зависимости от начального числа степеней свободы (принимается по табл. 6).
минимально допустимая теоретическая частота крайних классов в зависимости от начального числа степеней свободы (принимается по табл. 6). , (24)
, (24) (12)
(12) , приходящихся на каждый интервал.
, приходящихся на каждый интервал.
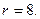



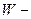 полусумма начала данного класса и начала следующего класса. Середины крайних классов принимаем близкими к наименьшему и наибольшему значениям случайной величины.
полусумма начала данного класса и начала следующего класса. Середины крайних классов принимаем близкими к наименьшему и наибольшему значениям случайной величины.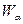 и конец
и конец  класса находим по формулам
класса находим по формулам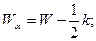

 принятая точность измерения случайной величины.
принятая точность измерения случайной величины.
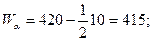

 …
… 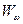

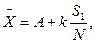 (13)
(13) условная средняя, середина модального или близкого к нему класса, принимаем
условная средняя, середина модального или близкого к нему класса, принимаем 
 420:
420: - первая сумма,
- первая сумма,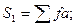
 условные отклонения середин классов, выраженные в
условные отклонения середин классов, выраженные в
 (14)
(14) сумма взвешенных квадратов центральных отклонений середин классов от средней ряда, выраженная в квадратах классовых промежутков,
сумма взвешенных квадратов центральных отклонений середин классов от средней ряда, выраженная в квадратах классовых промежутков,
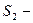 вторая сумма,
вторая сумма,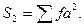

 ,
,  ,
, 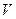





 (15)
(15)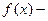 первая функция нормированного отклонения. Представляет собой нормальный закон распределения при
первая функция нормированного отклонения. Представляет собой нормальный закон распределения при 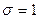 , значения его табулированы [1];
, значения его табулированы [1];