
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы распределения случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Наиболее часто встречаются законы равномерного, нормального и показательного распределения вероятностей непрерывных случайных величин. Равномерным называется распределение вероятностей непрерывной случайной величины Х, если на интервале (а,b), которому принадлежат все возможные значения Х, плотность распределения сохраняет постоянное значение Функция распределения имеет вид:
Нормальным называется распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид:
Вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (α; β):
где при Вероятность того, что абсолютная величина отклонения будет меньше положительного числа δ:
В частности, если а = 0, то Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью:
где λ – постоянная положительная величина. Функция распределения показательного закона:
Вероятность попадания непрерывной случайной величины Х в интервал (a, b), распределенной по показательному закону:
1 Случайная величина Х равномерно распределена в интервале (-2;N). Найти: а) дифференциальную функцию случайной величины Х; б) интегральную функцию случайной величины Х; в) вероятность попадания случайной величины в интервал 2 Найти математическое ожидание и дисперсию случайной величины, равномерно распределенной в интервале: а) (5; 11); б) (-3; 5). Начертить графики этих функций. 3 Случайная величина Х равномерно распределена в интервале (2; 6), причем Д(х) = 12. Найти функции распределения случайной величины Х. Начертить графики функций. 4 Для исследования продуктивности определенной породы домашней птицы измеряют диаметр яиц. Наибольший поперечный диаметр яиц представляет собой случайную величину, распределенную по нормальному закону со средним значением 5 см и средним квадратическим отклонением 0,3 см. Найти вероятность того, что: а) диаметр взятого наудачу яйца будет заключен в границах от 4,7 до 6,2 см; б) отклонение диаметра от среднего не превзойдет по абсолютной величине 0,6 см. 5 Вес вылавливаемых в пруду рыб подчиняется нормальному закону распределения со средним квадратическим отклонением 150 г и математическим ожиданием 1000 г. Найти вероятность того, что вес пойманной рыбы будет: а) от 900 до 1300 г; б) не более 1500 г; в) не менее 800 г; г) отличаться от среднего веса по модулю не более чем на 200 г; д) начертить график дифференциальной функции случайной величины Х. 6 Урожайность озимой пшеницы по совокупности участков распределяется по нормальному закону с параметрами: а = 50 ц/га, 7 Выборочным методом измеряется засоренность зерна, случайные ошибки измерения подчинены нормальному закону распределения со средним квадратическим отклонением 0,2 г и математическим ожиданием а = 0. Найти вероятность того, что из четырех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 0,3 г. 8 Количество зерна, собранного с каждой делянки опытного поля, есть нормально распределенная случайная величина Х, имеющая математическое ожидание 60 кг и среднее квадратическое отклонение 1,5 кг. Найти интервал, в котором с вероятностью 0,9906 будет заключена величина Х. Написать дифференциальную функцию этой случайной величины. 9 С вероятностью 0,9973 было установлено, что абсолютное отклонение живого веса случайно взятой головы крупного рогатого скота от среднего веса животного по всему стаду не превосходит 30 кг. Найти среднее квадратическое отклонение живого веса скота, считая, что распределение скота по живому весу подчиняется нормальному закону. 10 Урожайность овощей по участкам является нормально-распределенной случайной величиной с математическим ожиданием 300 ц/га и средним квадратическим отклонением 30 ц/га. С вероятностью 0,9545 определить границы, в которых будет находиться средняя урожайность овощей на участках. 11 Нормально-распределенная случайная величина Х задана дифференциальной функцией:
Определить: а) вероятность попадания случайной величины в интервал (3; 9); б) моду и медиану случайной величины Х. 12 Торговая фирма продает однотипные изделия двух производителей. Срок службы изделий подчиняется нормальному закону. Средний срок службы изделий первого производителя составляет 5,5 тыс. часов, а второго 6 тыс. часов. Первый производитель утверждает, что с вероятностью 0,95 срок службы его изделия находится в границах от 5 до 6 тыс. часов, а второй, с вероятностью 0,9, в границах от 5 до 7 тыс. часов. Изделия какого производителя имеют большую колеблемость срока службы. 13 Месячная заработная плата работников предприятия распределяется по нормальному закону с математическим ожиданием а = 10 тыс. руб. Известно, что 50 % работников предприятия получает заработную плату от 8 до 12 тыс. руб. Определить, какой процент работников предприятия имеет месячную заработную плату от 9 до 18 тыс. руб. 14 Написать плотность и функцию распределения показательного закона, если: а) параметр 15 Случайная величина Х распределена по показательному закону, причем 16 Найти М(Х), Д(Х),
если: а) 17 Испытываются два независимо работающих элемента. Длительность безотказной работы первого имеет показательнее распределение 18 Вероятность того, что оба независимых элемента будут работать в течении 10 суток равна 0,64. Определить функцию надежности для каждого элемента, если функции одинаковы. 19 Среднее число ошибок, которые делает оператор в течение часа работы равно 2. Найти вероятность того, что за 3 часа работы оператор сделает: а) 4 ошибки; б) не менее двух ошибок; в) хотя бы одну ошибку. 20 Среднее число вызовов, поступающих на АТС в одну минуту, равно трем. Найти вероятность того, что за 2 минуты поступит: а) 4 вызова; б) не менее трех вызовов. 21 Случайная величина Х распределена по закону Коши
Определить: а) интегральную функцию случайной величины Х; б) вероятность попадания случайной величины в интервал (- 22 Случайная величина Х распределена по закону Релея
Найти: а) дифференциальную функцию случайной величины Х; б) вероятность попадания случайной величины в интервал (1; 2), при а = 1; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 23 Функция распределения годовых доходов лиц, облагаемых налогом, имеет вид:
Определить: а) размер годового дохода, который для случайно взятого лица будет превышен с вероятностью 0,8; б) дифференциальную функцию случайной величины Х; в) математическое ожидание случайной величины Х, при 24 Случайная величина Х распределена по закону прямоугольного треугольника (рис. 1) в интервале (0; а). Найти: а) дифференциальную функцию случайной величины Х; б) интегральную функцию; в) вероят- ность попадания случайной величины в интервал ( ожидание, дисперсию и среднее квад- ратическое отклонение случайной величины Х.
0 а х Рисунок 1. 25 Случайная величина Х распределена по закону Симпсона («закону равнобедренного треугольника») (Рис. 2) на интервале (-а; а). Найти: а) дифференциальную функцию распределения вероятностей случайной величины Х; f(x) б) интегральную функцию и построить ее график; в) вероятность попадания случайной величины в интервал (- Рисунок 2.
ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН а) Функция одного случайного аргумента. Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины У, то У называют функцией случайного аргумента Х. У = φ(Х). Пусть аргумент Х Если аргумент Х принимает значение хi с вероятностью Рxi, то случайная величина У принимает значение Пусть аргумент Х – непрерывная случайная величина, заданная плотностью распределения f(x). Если у = φ(х) – дифференцируемая, строго возрастающая или строго убывающая функция, обратная функция которой х = ψ(y), то плотность распределения g(у) случайной величины У находится:
Если функция У = φ(Х) в интервале возможных значений Х не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция φ(х) монотонна, и найти плотности распределения gi(у) для каждого из интервалов монотонности, а затем представить g(у) в виде суммы:
Например, если функция φ(х) монотонна на двух интервалах, в которых соответствующие обратные функции
б) Функция двух случайных аргументов. Если каждой паре возможных значений случайных величин Х и У соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов Х и У.
Если Х и У – дискретные независимые случайные величины, то для того чтобы найти распределение функции Z = X + Y надо найти все возможные значения Если Х и У – непрерывные случайные величины, то плотность распределения g(z) суммы Z = X + Y, при условии, что плотность распределения хотя бы одного из аргументов задана в интервале (- ∞; ∞), находится по формуле:
где f1 и f2 – плотности распределения аргументов Х и У. Если возможные значения аргументов неотрицательны, то плотность распределения g(z) величины Z = X + Y находят по формуле:
Если Х и У – независимые случайные величины, заданные соответствующими плотностями распределения
1. Дискретная случайная величина задана законом распределения:
Найти закон распределения случайной величины У, где: а) У=2Х-1; б) У=Х+5; в) У=Х2-2; г) У=
2. Дискретная случайная величина Х задана законом распределения:
Найти закон распределения случайной величины У, где: а) У=2Х+1; б)У=Х3-1; в) У=Х2; г) У=
3. Дискретная случайная величина Х задана законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины У, если: а) У=4Х-4; б) У=Х2.
4. Дискретная случайная величина Х задана законом распределения:
Найти: а) закон распределения случайной величины У=sin2 X; б) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины У. 5. Случайная величина Х равномерно распределена на интервале (2;10). Найти дифференциальную функцию случайной величины: а) Y = 0,5 X – 1; б) Y = X2; в) 6. Случайная величина Х равномерно распределена в интервале (- а) Y = sin X; б) У= cos X. 7. Случайная величина Х распределена нормально с параметрами а = 2, а) У=2Х+6; б) У=Х3. 8. Непрерывная случайная величина Х задана функцией
Найти дифференциальную функцию случайной величины: а) 9. Сторона квадрата Х имеет равномерное распределение на отрезке [1;2]. Найти плотность вероятности площади квадрата. 10. Случайная величина Х распределена по закону Коши:
Найти дифференциальную функцию случайной величины: а) У=Х3; б) У=3Х. 11. Независимые случайные величины Х и У распределены равномерно. Случайная величина Х распределена в интервале (0; 2), а случайная величина У в интервале (0; 10). Найти интегральную и дифференциальную функции случайной величины Z=X+У. Построить графики интегральной и дифференциальной функций случайной величины Z. 12. Случайная величина Х равномерно распределена в интервале (-4; 1), а случайная величина У равномерно распределена в интервале (1; 6). Найти дифференциальную функцию случайной величины Z=X+У и начертить ее график. 13. Независимые случайные величины Х и У заданы дифференциальными функциями:
Найти дифференциальную функцию случайной величины Z=X+У. 14. Независимые случайные величины Х и У распределены по нормальному закону:
Найти дифференциальную функцию случайной величины Z=X+У. Показать, что случайная величина Z распределяется по нормальному закону. 15. Натуральный логарифм некоторой случайной величины Х распределен по нормальному закону с центром рассеивания
ЗАКОН БОЛЬШИХ ЧИСЕЛ
Закон больших чисел представляет собой наиболее общий принцип, в результате которого количественные закономерности, присущие массовым случайным явлениям, отчетливо проявляются при достаточно большом числе наблюдений. Лемма Чебышева. Если все значения случайной величины Х неотрицательны, то вероятность того, что случайная величина Х будет не меньше некоторого числа t > 0 не больше, чем
Неравенство Чебышева. Вероятность того, что абсолютное отклонение случайной величины Х от ее математического ожидания меньше некоторого числа ε > 0, не меньше чем
Теорема Чебышева. Если попарно – независимые случайные величины имеют конечные математические ожидания, дисперсии каждой из случайной величины не превосходят постоянного числа С, то среднее арифметическое этих величин сходится по вероятности к среднему арифметическому их математических ожиданий. Если
Воспользовавшись неравенством Чебышева, получаем
1 Цена акций коммерческой фирмы, реализуемых на фондовом рынке, является случайной величиной, математическое ожидание которой равно 6 тыс. руб. Оценить вероятность того, что в ближайшие сутки цена акций превысит 10 тыс. руб. 2 Количество электроэнергии, потребляемой поселком в течении суток, является случайной величиной, математическое ожидание которой равно 4 тыс. кВт.- ч. Оценить вероятность того, что в ближайшие сутки потребление энергии: а) превысит 8 тыс. кВт.- ч.; б) не превысит 6 тыс. кВт.- ч. 3 Пользуясь неравенством Чебышева, оценить вероятность того, что из посеянных 5000 семян число взошедших окажется от 3750 до 4250, если известно, что М(Х) = 4000. Определить вероятность попадания случайной величины в данный интервал. 4 Вероятность вызревания семян овощной культуры в данной местности составляет 0,8. С помощью неравенства Чебышева оценить вероятность того, что из 1000 растений, число растений с вызревшими семенами составит от 750 до 850. Определить вероятность попадания случайной величины в данный интервал. 5 В организации имеется 100 автомобилей. Вероятность безотказной работы каждого из них в течение определенного времени составляет 0,9. С помощью неравенства Чебышева оценить вероятность того, что: а) отклонение числа безотказно работавших автомобилей за определенный период времени от его математического ожидания не превзойдет по модулю 5; б) отклонение доли безотказно работающих автомобилей от постоянной вероятности 0,9 по модулю будет меньше 0,06. 6 Дискретная случайная величина Х задана законом распределения:
Используя неравенство Чебышева, оценить вероятность того, что
8 Дискретная случайная величина Х задана законом распределения:
Используя неравенство Чебышева, оценить вероятность того, что
9 Случайная величина Х задана дифференциальной функцией:
а) С помощью неравенства Чебышева оценить вероятность того, что 10 Случайная величина задана интегральной функцией:
а) С помощью неравенства Чебышева оценить вероятность того, что
11 Случайная величина задана интегральной функцией
а) используя неравенство Чебышева, оценить вероятность того, что
12 Выборочным способом определяют вес колосьев ячменя. Сколько необходимо отобрать колосьев, чтобы с вероятностью не меньшей 0,99, можно было утверждать, что средний вес случайно отобранных колосьев будет отличаться от среднего веса колосьев во всей партии (принимаемого за математическое ожидание) не более чем на 0,1 г? Установлено, что среднее квадратическое отклонение веса не превышает 0,2 г. 13 Сколько человек необходимо отобрать для определения удельного веса лиц со специальным образованием, чтобы с вероятностью 0,95 можно было утверждать, что отклонение относительной частоты лиц со специальным образованием от их доли, принимаемой за постоянную вероятность, не превышало по модулю 0,04.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.012 с.) |

 (6.1)
(6.1) (6.2)
(6.2) . (6.3)
. (6.3) ,
,  . (6.4)
. (6.4) , (6.5)
, (6.5) - функция Лапласа, причем
- функция Лапласа, причем  ,
, .
. . (6.6)
. (6.6) . (6.7)
. (6.7) (6.8)
(6.8) (6.9)
(6.9) . (6.10)
. (6.10) . (6.11)
. (6.11) ; г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
; г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. = 10 ц/га. Определить: а) какой процент участков будет иметь урожайность свыше 40 ц/га; б) процент участков с урожайность от 45 до 60 ц/га.
= 10 ц/га. Определить: а) какой процент участков будет иметь урожайность свыше 40 ц/га; б) процент участков с урожайность от 45 до 60 ц/га. .
. ; б)
; б)  ; в)
; в)  . Начертить графики функций.
. Начертить графики функций.
 ; б)
; б)  ; в)
; в)  .
. , второго
, второго 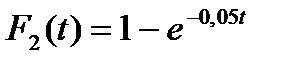 . Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент; в) откажет хотя бы один элемент; г) оба элемента откажут.
. Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент; в) откажет хотя бы один элемент; г) оба элемента откажут. .
.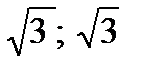 ).
).

 .
. ); г) математическое
); г) математическое ); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. дискретная случайная величина. Тогда случайная величина У = φ(Х) также дискретная случайная величина.
дискретная случайная величина. Тогда случайная величина У = φ(Х) также дискретная случайная величина. с той же вероятностью
с той же вероятностью 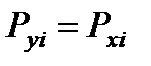 .
. . (7.1)
. (7.1) . (7/2)
. (7/2) и
и  то
то . (7.3)
. (7.3) . (7/4)
. (7/4) и их вероятности
и их вероятности  .
.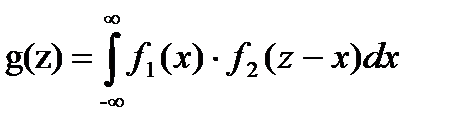 , или
, или  , (7.5)
, (7.5) , или
, или  . (7.6)
. (7.6)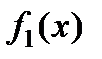 и
и  , то вероятность попадания случайной точки (Х, У) в область S равна:
, то вероятность попадания случайной точки (Х, У) в область S равна: . (7.7)
. (7.7) . Определить М(У).
. Определить М(У).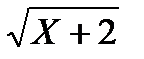 . Определить М(У).
. Определить М(У).


 . Определить М(У), Д(У), σ(У).
. Определить М(У), Д(У), σ(У).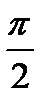 ;
;  ). Найти дифференциальную функцию случайной величины:
). Найти дифференциальную функцию случайной величины: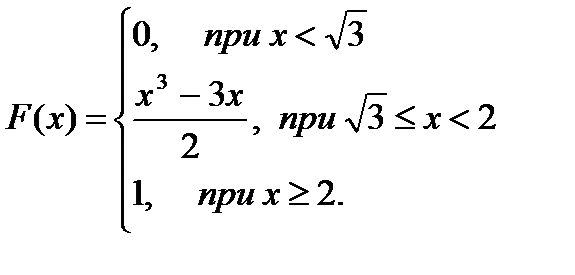
 ; б)
; б)  .
. .
.
 ,
,  .
.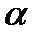 и средним квадратическим отклонением
и средним квадратическим отклонением 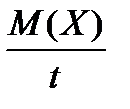 .
. . (8.1)
. (8.1) .
. . (8.2)
. (8.2) , то
, то . (8.3)
. (8.3)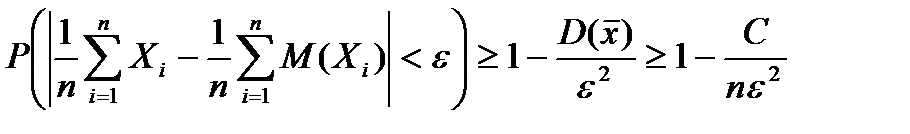 . (8.4)
. (8.4)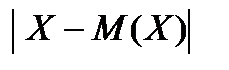 >3.
>3.
 . б) Определить вероятность того, что
. б) Определить вероятность того, что 
 . б) Определить вероятность того, что
. б) Определить вероятность того, что 



