
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительные величины. Относительная величина структуры. Относительная величина интенсивности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вопросы к экзамену по «Статистика и бух. учёт». Аналитическая группировка. Статистическая группировка – это один из основных этапов проведения статистического исследования. Процесс образования однородных групп на основе разделения статистической совокупности на части или объединение изучаемых статистических единиц в совокупности по определенным для них признакам называют статистической группировкой. Важнейшим статистическим методом обобщения данных являются статистические группировки. Различают следующие виды статистических группировок: 1) типологические; 2) структурные; 3) аналитические. Качественно однородные группы совокупностей, называют типологической группировкой. Для построения типологической группировки необходимо воспользоваться количественными и качественными (атрибутивными) признаками. Разделение однородной совокупности на определенные группы, которые в дальнейшем будут характеризовать структуру по определенному группировочному признаку, называют структурной группировкой. Здесь также рассматриваются количественные и атрибутивные признаки. Основная задача статистических группировок – исследование связей и зависимостей между признаками единиц статистической совокупности, которая решается с помощью построения аналитических группировок. Аналитическая группировка – это группировка, выявляющая взаимосвязи и взаимозависимости между изучаемыми социально-экономическими явлениями и признаками, их характеризующими. Все признаки в статистической науке можно подразделять на факторные и результативные. Признаки, которые оказывают большое влияние на изменение результативных признаков, называют факторными. Признаки, изменяющиеся под влиянием факторных признаков, называют результативными. Простой называется группировка, если группа образована только по одному признаку. Если разбить группу на подгруппу в соответствии с определенными признаками, то такую группировку называют комбинированной. Различают группировки по используемой информации: 1) первичные – производятся на основе исходных данных, которые были получены в результате статистического наблюдения; 2) вторичные – это результат соединения или расчленения группировки. Аналитические группировки служат для выявления аналитической зависимости между группировочными признаками. При построении аналитических группировок важно правильно определить признак-результат и признак-фактор. Признак, влияние которого на другие признаки исследуется, называется признаком-фактором. Признак, испытывающий влияние факторного, называется признаком-результатом. Чтобы установить связь между признаками, аналитическая группировка осуществляется по признаку-фактору. Затем по каждой группе отбираются соответствующие значения признака-результата и рассчитывается его среднее значение. Сопоставляя изменение средних значений признака-результата от группы к группе с изменениями признака-фактора можно сделать вывод о наличии или отсутствии взаимосвязи, а также о ее направлении. Различие групповых средних позволяет утверждать, что признаки взаимозависимы. Если изменение величины признака-фактора в определенном направлении вызывает изменение величины признака-результата в том же направлении, то связь прямая, в противном случае — связь обратная. Макет таблицы для представления результатов аналитической группировки может выглядеть следующим образом: Наименование таблицы
Аналитические группировки Их задача – выявления влияния одних признаков на другие (выявить связь между социально-экономическими явлениями).
Абсолютные величины. Статистические данные, полученные при наблюдении, в результате сводки, группировки, почти всегда являются абсолютными величинами, т. е. величинами, которые выражены в натуральных единицах и получены в результате счета или непосредственного измерения. Абсолютные величины отражают численность единиц изучаемых совокупностей, размеры или уровни признаков, зарегистрированных у отдельных единиц совокупности, и общий объем количественно выраженного признака как результат суммирования всех его отдельных значений. Абсолютные величины имеют большое познавательное значение. Абсолютные величины выражают размеры (уровни, объемы) социально-экономических явлений и процессов, их получают в результате статистического наблюдения и сводки исходной информации. Абсолютные величины используют в практике торговли, применяют в анализе и прогнозировании коммерческой деятельности. На основе этих величин в коммерческой деятельности составляют хозяйственные договоры, оценивают объем спроса на конкретные изделия и т. д. Абсолютными величинами измеряются все стороны общественной жизни. Абсолютные величины по способу выражения размеров изучаемых процессов подразделяются на: индивидуальные и суммарные, они в свою очередь относятся к одному из видов обобщающих величин. Размеры количественных признаков у каждой статистической единицы характеризуют индивидуальные абсолютные величины, а также они являются базой при статистической сводке для соединения отдельных единиц статистического объекта в группы. На их основе получают абсолютные величины, в которых можно выделить показатели объема признаков совокупности и показатели численности совокупности. Если заняться исследованием развития торговли и ее состояния в определенном районе, то определенное количество фирм можно отнести к индивидуальным величинам, а объем товарооборота и число работников, работающих в фирме, относят к суммарным. Абсолютные величины бывают экономически простыми (численность магазинов, работников) и экономически сложными (объем товарооборота, размер основных фондов). Абсолютные величины – всегда числа именованные, имеют определенную размерность, единицы измерения. В статистической науке применяются натуральные, денежные (стоимостные) и трудовые единицы измерения. Единицы измерения называют натуральными, если они будут соответствовать потребительским или природным свойствам предмета, товара и будут выражены в физических весах, мерах длины и т. п. В статистической практике натуральные единицы измерения могут быть составными. Применяют условно-натуральные единицы измерения при суммировании количества разнородных товаров, продуктов. Абсолютные статистические величины Абсолютные статистические величины показывают объем, размеры, уровни различных социально-экономических явлений и процессов. Они отражают уровни в физических мерах объема, веса и т.п. В общем абсолютные статистические величины – это именованные числа. Они всегда имеют определенную размерность и единицы измерения. Последние определяют сущность абсолютной величины. Типы абсолютных величин 1. Натуральные – такие единицы, которые отражают величину предметов, вещей в физических мерах (вес, объем, площадь и т.д.). 2. Денежные (стоимостные) – используются для характеристики многих экономических показателей в стоимостном выражении. 3. Трудовые – используются для определения затрат труда (человеко-час, человеко-день) 4. Условно-натуральные –единицы, которые используются для сведения воедино нескольких разновидностей потребительных стоимостей (т.у.т = 29,3 МДж/кг; мыло 40 % жирности). Виды абсолютных величин – Индивидуальные – отражают размеры количественных признаков у отдельных единиц изучаемой совокупности. – Общие – выражают размеры, величину количественных признаков у всей изучаемой совокупности в целом. Абсолютные величины отражают наличие тех или иных ресурсов, это основа материального учета. Они наиболее объективно отражают развитие экономики. Абсолютные величины являются основой для расчета разных относительных статистических показателей.
Средняя геометрическая Если имеется n коэффициентов роста, то формула среднего коэффициента:
Это формула средней геометрической. Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего. Если осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Например, с помощью средней квадратической можно определить диаметры труб, колес и т. д. Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число.
Средние величины. Мода. Средняя величина – это обобщающая характеристика единиц совокупности по какому-либо варьирующему признаку. Средняя величина – это один из распространенных приемов обобщений. Средние величины позволяют сравнивать уровни одного и того же признака в различных совокупностях и находить причины этих расхождений. В анализе изучаемых явлений роль средних величин огромна. Средняя величина приобретает особую значимость в условиях рыночной экономики. Она помогает определить необходимое и общее, тенденцию закономерности экономического развития непосредственно через единичное и случайное. Средние величины – это обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления. Статистические средние величины рассчитываются на основе массовых данных статистически правильно организованного массового наблюдения. Если статистическая средняя рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений), то она будет объективной. Средняя величина абстрактна, так как характеризует значение абстрактной единицы. Средние величины должны применяться исходя из диалектического понимания категорий индивидуального и общего, единичного и массового. Средняя отображает что-то общее, которое складывается в определенном единичном объекте. В средней величине отражается характерный, типичный, реальный уровень изучаемых явлений. Задачей средних величин является характеристика этих уровней и их изменений во времени и пространстве. Средний показатель – это обычное значение, потому что формируется в нормальных, естественных, общих условиях существования конкретного массового явления, рассматриваемого в целом. Объективное свойство статистического процесса или явления отражает средняя величина. Индивидуальные значения исследуемого статистического признака у каждой единицы совокупности различны. Одни индивидуальные явления имеют признаки, которые существуют во всех явлениях, но в разных количествах – это рост или возраст человека. Другие признаки индивидуального явления, качественно различные в различных явлениях, т. е. имеются у одних и не наблюдаются у других (мужчина не станет женщиной). Средняя величина вычисляется для признаков качественно однородных и различных только количественно, которые присущи всем явлениям в данной совокупности. Средняя величина является отражением значений изучаемого признака и измеряется в той же размерности, что и этот признак. Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана. Мода (Мо) – чаще всего встречающийся вариант. Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений. Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность). В пределах интервала надо найти то значение признака, которое является модой.
где x0 – нижняя граница модального интервала; h – величина модального интервала; fm – частота модального интервала; f m -1 – частота интервала, предшествующего модальному; f m + 1 – частота интервала, следующего за модальным. Мода зависит от величины групп, от точного положения границ групп. Мода – число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя). Средние величины. Медиана. Средняя величина – это обобщающая характеристика единиц совокупности по какому-либо варьирующему признаку. Средняя величина – это один из распространенных приемов обобщений. Средние величины позволяют сравнивать уровни одного и того же признака в различных совокупностях и находить причины этих расхождений. В анализе изучаемых явлений роль средних величин огромна. Средняя величина приобретает особую значимость в условиях рыночной экономики. Она помогает определить необходимое и общее, тенденцию закономерности экономического развития непосредственно через единичное и случайное. Средние величины – это обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления. Статистические средние величины рассчитываются на основе массовых данных статистически правильно организованного массового наблюдения. Если статистическая средняя рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений), то она будет объективной. Средняя величина абстрактна, так как характеризует значение абстрактной единицы. Средние величины должны применяться исходя из диалектического понимания категорий индивидуального и общего, единичного и массового. Средняя отображает что-то общее, которое складывается в определенном единичном объекте. В средней величине отражается характерный, типичный, реальный уровень изучаемых явлений. Задачей средних величин является характеристика этих уровней и их изменений во времени и пространстве. Средний показатель – это обычное значение, потому что формируется в нормальных, естественных, общих условиях существования конкретного массового явления, рассматриваемого в целом. Объективное свойство статистического процесса или явления отражает средняя величина. Индивидуальные значения исследуемого статистического признака у каждой единицы совокупности различны. Одни индивидуальные явления имеют признаки, которые существуют во всех явлениях, но в разных количествах – это рост или возраст человека. Другие признаки индивидуального явления, качественно различные в различных явлениях, т. е. имеются у одних и не наблюдаются у других (мужчина не станет женщиной). Средняя величина вычисляется для признаков качественно однородных и различных только количественно, которые присущи всем явлениям в данной совокупности. Средняя величина является отражением значений изучаемого признака и измеряется в той же размерности, что и этот признак. Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана. Медиана (Me) – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие. Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних. Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал:
iMe – величина медианного интервала; f/2 – полусумма частот ряда; SMe —1 – сумма накопленных частот, предшествующих медианному интервалу; fMe – частота медианного интервала. Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности. Коэффициент вариации. Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Колебания отдельных значений характеризуют показатели вариации. Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую. Основными критериями разнообразия признака в статистической совокупности являются: квадратическое отклонение и коэффициент вариации. Определение перечисленных критериев разнообразия признака прежде всего осуществляется с учетом его значения у отдельных элементов статистической совокупности. Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два ряда распределения, имеющих одинаковую среднюю арифметическую величину, могут значительно отличаться друг от друга по степени колеблемости (вариации) величины изучаемого признака. Если индивидуальные значения признака ряда мало отличаются друг от друга, то средняя арифметическая будет достаточно показательной характеристикой данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено. Значение показателей вариации заключается в следующем:
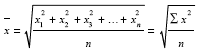
Для измерения вариации признака в рядах распределения применяются различные абсолютные и относительные показатели. В статистике чаще всего применяются следующие показатели (меры) вариации: среднее квадратическое отклонение и коэффициент вариации. Рассмотрим подробно каждый из перечисленных показателей вариации. Среднее квадратическое отклонение определяется как корень квадратный из среднего квадратов отклонений индивидуальных значений признака от средней арифметической и рассчитывается по следующим формулам:
для сгруппированных данных:
для интервального ряда:
Возведение индивидуальных отклонений в квадрат и последующее извлечение квадратного корня вызвано, как уже говорилось, тем, что суммирование отклонений в первой степени приводит к нулевому результату. Среднее квадратическое отклонение является общепринятым показателем вариации: при его определении принимаются в расчет все отклонения значений варьирующего признака от среднего. Проиллюстрируем расчет среднего квадратического отклонения для ранжированного и интервального вариационных рядов. Пример. Пусть испытываются шесть лампочек на продолжение горения. Результаты испытания представлены в табл. 6.3 (дискретный вариационный ряд). Таблица 6.3 Результаты испытаний лампочек
Рассчитаем среднюю арифметическую и среднее квадратическое отклонение:
Это означает, что в среднем продолжительность горения лампочки в изучаемой совокупности отклонялась от средней продолжительности в целом по совокупности на 14,3 часа. Пример. Рассчитаем среднее квадратическое отклонение срока обращения облигаций. Исходные данные для расчета и промежуточные вычисления представлены в табл. 6.4 (интервальный вариационный ряд). Рассчитаем среднюю арифметическую величину срока обращения акций и среднее квадратическое отклонение:
Таблица 6.4 Срок обращения облигаций
Среднее квадратическое отклонение – наиболее широко применяемые показатели вариации. Объясняется это тем, что оно входит в большинство теорем теории вероятности, служащих фундаментом математической статистики. Рассмотренные ранее показатели вариации. Так, например, среднее квадратическое отклонение урожайности пшеницы измеряется в центнерах. Так как среднеквадратическое отклонение – число именованное, то оно неудобно для сопоставления вариации различных признаков. Например, вычислив среднее квадратическое отклонение производительности работы и заработной платы рабочих, невозможно определить, вариация какого признака больше, т.к в первом случае она измеряется в единицах продукции (деталях), во втором – в рублях.
Принцип построения коэффициентов вариации таков
Чаще всего на практике употребляется квадратический коэффициент вариации. С помощью коэффициента вариации можно сравнивать размеры одного признака в нескольких совокупностях. Так, например, с помощью коэффициента вариации можно сравнивать вариацию срока службы станков на различных предприятиях, вариацию роста и веса населения в различных регионах страны. Пример. Рассмотрим коэффициенты вариации срока службы электролампочек, выпускаемых на трех заводах. Исходные данные представлены в табл. 6.5. Таблица 6.5 Срок службы электролампочек
Вычислим среднюю арифметическую срока горения лампочек:
Вычислим среднее квадратическое отклонение:
Вычислим коэффициент вариации для каждого завода и занесем данные в таблицу. Наиболее низкий коэффициент вариации у электролампочек, выпускаемых на заводе № 2, что свидетельствует о большой однородности его продукции (в данном случае, однородности качества электролампочек). Наиболее полную характеристику разнообразия признака в статистической совокупности дает среднее квадратическое отклонение В основе среднего квадратического отклонения лежит сопоставление каждой варианты Смыкание рядов динамики В большинстве случаев уровни ряда приводятся к сопоставимому уровню путем пересчета. Например может использоваться метод смыкания.
Суть метода заключается в том, что уровень 1994 г. принимается за 100 %, а затем производим соответствующий пересчет. Получаем ряд относительных величин. Средний уровень ряда. Показывает, какова средняя величина уровня, характерного для всего периода. Имеет смысл рассчитывать, когда величина изменения ряда более или менее стабильна. Средний уровень ряда исчисляется по средней хронологической. Ее расчет для интервального и моментного ряда имеет свои особенности. Для интервального ряда, уровни которого можно суммировать, можно исчислять по средней арифметической простой. Для моментного ряда с равноотстоящими уровнями: Для моментного ряда с неравноотстоящими интервалами: Например, даны следующие данные: 01.01.98 – 455 01.07 – 465 01.11 – 495 01.01.99 – 505 01.05 – 465 01.10 – 485 01.12 – 505 Абсолютный прирост Характеризует размер увеличения (уменьшения) уровней ряда за отдельный промежуток времени. Абсолютные приросты могут быть цепными или базисными. Цепной: Базисный: Средний абсолютный прирост Показывает скорость развития явления в изучаемом динамическом ряду. Он получается из абсолютных приростов как их средняя арифметическая. Может быть получен также как отношение абсолютного прироста за весь период к числу уровней без одного. Ряды динамики. Темп роста. Смыкание рядов динамики В большинстве случаев уровни ряда приводятся к сопоставимому уровню путем пересчета. Например может использоваться метод смыкания.
Суть метода заключается в том, что уровень 1994 г. принимается за 100 %, а затем производим соответствующий пересчет. Получаем ряд относительных величин. Средний уровень ряда. Показывает, какова средняя величина уровня, характерного для всего периода. Имеет смысл рассчитывать, когда величина изменения ряда более или менее стабильна. Средний уровень ряда исчисляется по средней хронологической. Ее расчет для интервального и моментного ряда имеет свои особенности. Для интервального ряда, уровни которого можно суммировать, можно исчислять по средней арифметической простой. Для моментного ряда с равноотстоящими уровнями: Для моментного ряда с неравноотстоящими интервалами: Например, даны следующие данные: 01.01.98 – 455 01.07 – 465 01.11 – 495 01.01.99 – 505 01.05 – 465 01.10 – 485 01.12 – 505 Темп роста Показывает, во сколько раз данный уровень ряда больше или меньше базисного уровня. Представляет собой соотношение двух сравниваемых уровней. Цепной: Базисный: Темпы роста выражаются либо в виде процентов, либо в виде коэффициентов. Если темп роста больше единицы (100%), то уровень ряда возрастает, если меньше – то убывает.
Смыкание рядов динамики В большинстве случаев уровни ряда приводятся к сопоставимому уровню путем пересчета. Например может использоваться метод смыкания.
Суть метода заключается в том, что уровень 1994 г. принимается за 100 %, а затем производим соответствующий пересчет. Получаем ряд относительных величин. Средний уровень ряда. Показывает, какова средняя величина уровня, характерного для всего периода. Имеет смысл рассчитывать, когда величина изменения ряда более или менее стабильна. Средний уровень ряда исчисляется по средней хронологической. Ее расчет для интервального и моментного ряда имеет свои особенности. Для интервального ряда, уровни которого можно суммировать, можно исчислять по средней арифметической простой. Для моментного ряда с равноотстоящими уровнями: Для моментного ряда с неравноотстоящими интервалами: Например, даны следующие данные: 01.01.98 – 455 01.07 – 465 01.11 – 495 01.01.99 – 505 01.05 – 465 01.10 – 485 01.12 – 505 Темп прироста Показывает, на какую долю (процент) уровень данного периода или момента времени больше или меньше базового уровня. Темп прироста может быть измерен и как отношение абсолютного прироста к базовому уровню. Средний абсолютный прирост Показывает скорость развития явления в изучаемом динамическом ряду. Он получается из абсолютных приростов как их средняя арифметическая. Может быть получен также как отношение абсолютного прироста за весь период к числу уровней без одного.
Оборотные активы. 1. Запасы: сырье, материалы и аналогичные ценности; затраты в незавершенном производстве; готовая продукция, товары для перепродажи и отгруженные; расходы будущих периодов. 2. Дебиторская задолженность: покупатели и заказчики; векселя к получению; задолженность дочерних и зависимых обществ; задолженность участников по вкладам в уставный капитал. 3. Финансовые вложения: займы, предоставленные организацией на срок менее 12 месяцев; собственные акции, выкупленные у акционеров; финансовые вложения. 4. Денежные средства: расчетные счета; валютные счета; денежные средства. Пассив. Капитал и резервы. Уставной капитал. Добавочный капитал. Резервный капитал: резервы, образованные в соответствии с законодательством и учредительными документами. Нераспределенная прибыль. Долгосрочные обязательства. 1. Заемные средства: кредиты, подлежащие погашению более чем через 12 месяцев после отчетной даты; займы, подлежащие погашению более чем через 12 месяцев после отчетной даты. 2. Прочие обязательства. Требования и основания проведения инвентаризации 1. Основания проведения инвентаризации: 1) передача имущества в аренду, выкуп, продажа, преобразование унитарного предприятия; 2) составление годовой бухгалтерской отчетности; 3) смена материально ответственных лиц; 4) выявление фактов хищен |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.014 с.) |

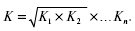

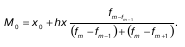
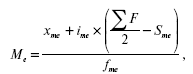 где хме – нижняя граница медианного интервала;
где хме – нижняя граница медианного интервала;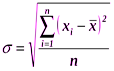 для не сгруппированных данных:
для не сгруппированных данных: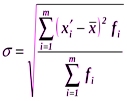

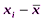
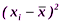
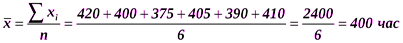
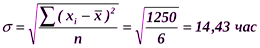
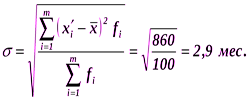
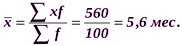 ;
;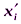
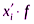
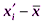
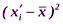
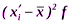
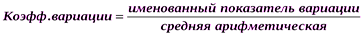 Для сравнения вариации разных признаков наиболее часто применяется показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности статистической совокупности. Статистическая совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному закону).
Для сравнения вариации разных признаков наиболее часто применяется показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности статистической совокупности. Статистическая совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному закону).
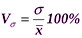
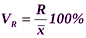
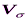 , %
, %
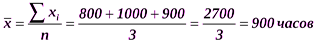 .
. .
.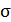 (сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением.
(сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением.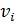 со средней арифметической
со средней арифметической 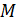 данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений
данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений  , имеющих знак "
, имеющих знак " 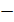 ", будет погашаться суммой отклонений, имеющих знак "
", будет погашаться суммой отклонений, имеющих знак " 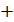 ", т.е. сумма всех отклонений
", т.е. сумма всех отклонений 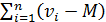 равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е.
равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е. 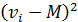 .
.


