
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Абсолютные и относительные статистические показатели.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Показатели, встречающиеся в статистической практике, можно разделить на группы по следующим признакам: 1. по сущности изучаемых явлений - объемные (количественные) характеризующие размер (объем) процесса. - качественные выражающие количественные соотношения, типичные свойства изучаемых совокупностей. 2. по степени агрегирования явлений - индивидуальные. Характеризуют единичные процессы - обобщающие. Отображают совокупность в целом или некоторую ее часть. 3. в зависимости от характера изучаемых явлений - интервальные. Выражают развитие явлений за отдельные периоды (интервалы времени). - моментные. Отображают состояние явления на отдельную дату (момент времени).
Вопрос. Абсолютные величины и их основные виды.
Абсолютные величины, выражающие: размеры, уровни, объемы явлений и процессов, получают в результате статистического наблюдения и сводки исходной информации. По способу выражения размеры изучаемых явлений, абсолютные величины делятся: 1. индивидуальные 2. сводные (суммарные). СУММАРНЫЕ – это частный случай обобщающих величин. Иногда индивидуальные величины могут носить разностный характер. Абсолютные показатели всегда числа именованные, имеющие определенную размерность и единицу измерения. В зависимости от цели анализа применяются следующие единицы измерения: 1. натуральные. Соответствуют природным или потребительским свойствам предмета, и выражаются в физических мерах (вес, длина, площадь, объем). Иногда одной единицы измерения для характеристики явления недосточна, и применяются составные натуральные единицы (ткм). Так же в эту группу входят условно-натуральные измерители. Применяются, когда один продукт имеет несколько разновидностей, и определение общего объема возможно исходя из некоторого общего для всех разновидностей потребительского свойства. 2. стоимостные (денежные). Дают денежную оценку экономическим явлениям и процессам. 3. трудовые. Позволяют учитывать общие затраты труда на предприятиях и трудоемкость отдельных операций технологического процесса.
Вопрос. Относительные величины их значения и основные виды.
АНАЛИЗ – это, прежде всего сравнение и сопоставление. В результате получается качественная оценка экономических явлений, выраженная в виде относительных величин. ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА – это частное от деления двух статистических величин, характеризующая количественное соотношение между ними.
Если база сравнения принимается за единицу, то мы получаем коэффициент. Если база сравнения 100%, то мы получаем процент (кроме % могут быть промилле %о). Все относительные показатели делятся на следующие виды: 1. динамики. 2. плана. 3. реализации плана. 4. структуры. 5. координация. 6. сравнение. 7. интенсивности и уровня экономического развития. y1 – уровень исследуемого показателя, (текущий, фактический период) y0 – уровень этого же явления процесса в прошлом (базисный) ym – уровень показателя на данный период времени
Показывает, во сколько раз текущий показатель превышает предыдущий или какую долю показывает. Выраженный соотношением называется коэффициентом роста. Выраженный процентами называется динамикой роста.
= ОПД= ОПП*ОПРП
Сравнивая структуру одной и той же совокупности можно проследить изменения.
Обычно в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с той или иной точки зрения. В результате имеем, сколько единиц одной части приходится на одну единицу (или другое количество единиц другой части).
Лекция №3.
ОПИ – относительные показатели интенсивности. Показываю насколько широко распространено, изучаемое явление, в той или иной среде. Характеризуют отношение разноименных, но связанных между собой показателей.
ОПИ всегда именованные величины. Например, число врачей на 10000 населения. Частный случай ОПИ, относительные показатели экономического развития (ОПЭР) характеризуют некоторые макроэкономические показатели в расчете на душу населения.
ОПС – относительный показатель сравнения. Характеризует количественное соотношение одноименных показателей, относящихся к разным объектам наблюдения.
Вопрос.
СРЕДНЯЯ ВЕЛИЧИНА – обобщающий показатель, который выражает типичные черты и дает обобщающую количественную характеристику какого – либо уровня, какого – либо варьирующего признака по совокупности однородных явлений. Основные формулы для вычисления средних могут быть получены на основе формулы степенной средней.
х – осредняемый признак, тогда хj- варианты, fj – частоты или количество повторов индивидуальных значений признака. Виды средних величин: 1. простая или не взвешенная средняя. Применяется, если отдельные значения, изучаемые не повторяются. 2. взвешенные. Применяются, если отдельные значения в изучаемой совокупности повторяются.
Средняя арифметическая исчисляется в тех случаях, когда общий объем осредняемого признака образуется как сумма его значений об отдельных единиц совокупности. Например, требуется вычислить средний стаж работников. Их стаж xj – 6,5,4,3,3,4,5,4,5,4.
Чаще среднее рассчитывают по сгруппированным данным:
Получаем формулу средней арифметической:
Взвешенная средняя учитывает различные значения отдельных вариант в пределах совокупности. Поэтому применяется, если варианты имеют различную численность. Арифметическая средняя распределяет поровну между объектами общую величину признака. В качестве частот могут быть взяты не только абсолютные, но и относительные величины (частости).
Часто вычисления средней приходится производить по данным сгруппированным в виде интервальных рядов. При этом необходимо в каждом интервале определить серединное значение. А затем произвести взвешивание найденных значений обычным порядком. Иногда первые и последние интервалы могут быть открытыми (нет границ). Тогда при вычислении серединного значения предполагаем, что расстояние между границами данного интервала такое же как в соседнем. Например.
Изложенный выше метод является вынужденным, если нет прямых данных о величине конкретных вариантов. Метод основан на предположении, что отдельные варианты равномерно распределены внутри интервала. В действительности это может быть не так. Тогда середина интервала может отличаться от настоящей средней. Т.е. метод является приближенным. Степень расхождения зависит от следующих причин: 1. число вариант (n). Чем больше вариант, тем меньше ошибка. 2. величина интервала. Чем меньше величина интервалов, тем меньше ошибка. 3. характер распределения. Чем симметричней распределение, тем меньше ошибка. 4. принцип построения интервального ряда. При равных интервалах ошибка меньше. Наличие открытых интервалов может увеличивать ошибку.
Основные свойства средней арифметической: 1. от уменьшения или увеличения частот каждого значения признака, в одно и то же число раз, величина средней арифметической не изменится.
Именно это свойство позволяет при расчетах заменять абсолютные частоты относительными.
2. общий множитель можно выносить за знак средний
3. A* const, 4. все хj =c, c – const =>
5. Изложены свойства позволяют во многих случаях упростить среднее. Из каждого значения х вычитается некоторая постоянная величина. Полученные разности сокращают на общий множитель. Вычисляют среднюю.
Из таблицы (с 3 столбца). А – центральная варианта ряда. Если вариант 2, то ставится та, у которой большая частота. А=550 i – величина интервала i = 100
Лекция №4.
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ – величина, применяющаяся в случаях, когда исходная информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.
Например, по трем городам имеются данные о цене и сумме реализации некоторого товара.
Т.е. средняя гармоническая является превращенной формой средней арифметической.
Например, машина проехала путь в одну сторону со скоростью 80 км/ч, а в другую сторону этот же путь со скоростью 60 км/ч. Определить среднюю скорость.
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ – величина, используемая как средняя из отношений или в рядах распределения представленных в виде геометрической прогрессии. Например, среднегодовые темпы роста.
Структурные средние. Показатели: 1. мода. МОДА – значение признака, наиболее часто встречающееся в исследуемой совокупности. Например 2 – 0 3 – 13 4 – 32 5 – 10 Мода из ряда распределения оценок – 4.
2. медиана МЕДИАНА – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Для дискретных рядов распределения с нечетным числом членов медианой является варианта, стоящая в середине ранжированного ряда. Если ранжированный ряд имеет четное число элементов, то медианой будет среднее арифметическое из двух серединных величин. Медиана практически выполняет функцию средней для неоднородной неподчиняющейся нормальному закону распределения совокупности. Например, представим совокупность, в которой 99 человек имеют доход от 100 до 200 долларов, 1 – 50000
В среднем около 150 $
Рассмотрим на примере нахождение моды и медианы по сгруппированным данным. Имеются данные о тарифном разряде бригадным рабочим.
fmax=60 =>M0 = 5 разряд
Me = 4 разряд
В интервальных рядах распределения мода и медиана вычисляется на основе следующих формул:
Модальным является интервал с наибольшей частотой.
медианным является интервал, в котором впервые Например
Аналогично нахождение медианы можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на 4 части (квартили), на 5 частей (квинтили), на 10 частей (децили), на 100 частей (перцентели).
Лекция № 5. ПОКАЗАТЕЛИ ВАРИАЦИИ (§6) Различия индивидуальных значений признака внутри изучаемой совокупности называется ВАРИАЦИЕЙ ПРИЗНАКА. Она возникает в результате того, что индивидуальные значения складываются под влиянием разных факторов, условий, которые по-разному сочетаются отдельном случае. Средняя не дает представление о том, как отдельные значения признака группируются вокруг средней. Если отдельные значения близко примыкают к средней, то средняя хорошо представляет всю совокупность. Иначе нет. Колеблемость отдельных значений признака характеризуют показатели вариации. В статистике под вариацией понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию случайную и систематическую. Изучая систематическую вариацию можно оценить, насколько однородной является изучаемая совокупность в количественном, а иногда и качественном отношении, и насколько характерной для нее является исчисленная средняя.
§ 6.1. Абсолютные или средние показатели вариаций. Способы их расчета.
1. размах вариации Улавливает только крайние отклонения, не отражает всех вариант в ряду. 2. среднее линейное отклонение В качестве меры вариации признака применяют в статистической практики редко. Данный показатель во многих случаях не устанавливает степень рассеивания. 3. дисперсия (средний квадрат отклонений) 4. среднее квадратическое отклонение (СКО)
Свойства: 1. если к каждому значению вариант добавить (вычесть) одно и то же постоянное число, то дисперсия не изменится. 2. если каждое значение вариант увеличить (уменьшить) в k раз, то дисперсия увеличится или уменьшится в 3. если исчислить средний квадрат отклонений от любой величины, которая отличается от средней арифметической, он будет больше среднего квадрата отклонений от средней арифметической, т.е. больше дисперсии. 4. если все частоты признака увеличить (уменьшить) в одно и то же число раз, то дисперсия не изменится.
Изложенные свойства позволяют вывести формулу для вычисления дисперсии.
5. квартильное отклонение
§ 6.2. Показатели относительного рассеивания.
1. коэффициент осуилляции 2. относительное линейное отклонение (линейный коэффициент вариации)
3. коэффициент вариации Коэффициент вариации является критерием надежности средств. Если он меньше 33%, то можно говорить об однородности совокупности и надежности средней для этой совокупности, иначе наоборот (вытекает из правила 3х сигма в курсе теории вероятности). 4. коэффициент квартельной вариации 5. коэффициент децельной дифференциации
§ 6.3. Дисперсия альтернативного качественного признака
Обозначим наличие изучаемого признака цифрой 1, а отсутствие 0. Пусть доля единиц обладающих признаком составляет p, а не обладающих q. p+q=1.
§ 6.4. Виды дисперсий и правило их сложения
На ряду с изучением вариации признака по всей совокупности может возникнуть необходимость проследить количественные изменение признака, на которые они разбиты, а так же на группы. В этом случае различают дисперсию: 1. общую
2. внутригрупповую 3. межгрупповую
4. средняя из внутригрупповых
Закон сложения дисперсии
Эмпирический коэффициент детерминации
Показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака (часто измеряется в %). Эмпирическое корреляционное отношение
Говорят, что зависимость между результативным или группировочным признаками больше, если Лекция №6. §7 ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ. ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЯ. НОРМЫ РАСПРЕДЕЛЕНИЯ. В некоторых рядах распределения с увеличением значительного варьирующего признака частоты первоначально увеличиваются, а затем после достижения max значения в середине интервала, снижаются. Это свидетельствует о том, что частоты изменяются закономерно в связи с изменением признака. Такие явления называют ЗАКОНОМЕРНОСТЯМИ РАСПРЕДЕЛЕНИЯ. Одна из важнейших целей изучения статистических вариаций рядов - выявить законность распределения и определить ее характер. Как и все статистические законности, законности распределения проявляются в классовом числе наблюдений. При этом необходимо правильно построить вариационный ряд – определить оптимальное число групп и величину интервалов, при которых законности проявляются наиболее отчетливо, если трудно, то совокупность разбивается на max числа групп, затем, укрепление интервала и тем самым уменьшение числа групп, который характер распределения проявляется наиболее четко. Основная задача анализа вариационных рядов – выявить подлинную законность путем исключения влияния второстепенных, случайных для данного распределения фактов, достигается путем увеличения объема исследуемой совокупности при одновременном уменьшении интервала.
Истограмма
f3 →полигон f2
f1
x1 x2 x3 x4 х
Из математической статистики известно, что если увеличить объем совокупности и уменьшить интервалы группировки, то полигон распределения, все более и более приближен к плавной линии – КРИВОЙ РАСПРЕДЕЛЕНИЯ. ТЕОРИТИЧНОСТЬ КРИВОЙ РАСПРЕДЕЛЕНИЯ – называется кривая, сопровождающая общую закономерность данного типа распределения в чистом виде, исключая влияния случайных факторов, т.е. исследуемая эмпирическая модель сводится к идеализированной, теоретичности (а они в свою очередь хорошо изучены). Виды кривой распределения: 1. одновременные кривые - симметричные - условно симметричные - крайне симметричные 2. многовеличинные кривые Как правило, для однородных совокупностей характерны одновременные кривые. Многовероятность свидетельствует о неоднородности данных. При появлении 2х и более вершин необходимо провести перегруппировку с целью выявления однородных групп. Выяснение общего характера распространено предполагает выявление его однородности.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.191.241 (0.009 с.) |






 (yi : yj)
(yi : yj)

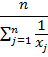
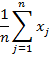



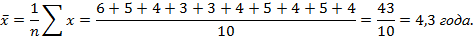
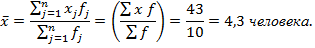





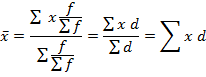



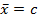

 .формула называется «Способ моментов или способ отсчета от условного нуля».
.формула называется «Способ моментов или способ отсчета от условного нуля».



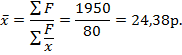


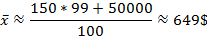




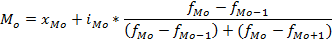


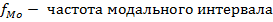

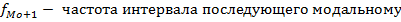
 , n- объем совокупности
, n- объем совокупности








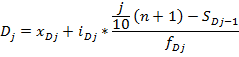
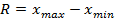

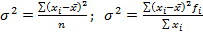

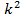 раз. А СКО в k раз.
раз. А СКО в k раз.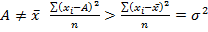


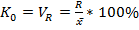
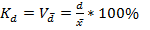





 суммирование идет по всей совокупности. Измеряет вариацию признака во всей совокупности под влиянием всех факторов обусловивших эту вариацию.
суммирование идет по всей совокупности. Измеряет вариацию признака во всей совокупности под влиянием всех факторов обусловивших эту вариацию.
 .
. – общее среднее по всей совокупности
– общее среднее по всей совокупности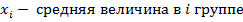


 - общая дисперсия
- общая дисперсия изменяется от 0 до 1 либо от 0 до 100%
изменяется от 0 до 1 либо от 0 до 100% изменяется в пределах от 0 до 1
изменяется в пределах от 0 до 1 больше 0,7.
больше 0,7.


