Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка результатов выборочного наблюдения и распространение их на генеральную совокупность.Содержание книги
Поиск на нашем сайте ЗАКЛЮЧИТЕЛЬНЫЙ ЭТАП ВЫБОРОЧНОГО НАБОЛЮДЕНИЯ – это распространение его результатов на генеральную совокупность. Обычно этому предшествует оценка результатов выборки с точки зрения самой возможности такого распространения. Вывод зависит во многом от качества основы выборки, прежде всего от ее полноты. Под полнотой подразумевается наличия или представленность всех групп или типов генеральной совокупности в основе выборки. Неполнота может привести к нарушению представительности выборки, и, как следствие, к неправильным выводам, при анализе ее данных. Вывод о возможности распространения результатов делается не только исходя из анализа исходных данных. Другой основой суждения может являться расчет относительной ошибки. Относительная ошибка для средней Для доли Если величина относительной ошибки не превышает заранее установленного значения, то данные выборочного наблюдения являются представительными, и могут быть распространены на генеральную совокупность. В противном случае, пытаются восстановить исходные пропорции генеральной совокупности. Этот процесс называется корректировкой или коррекцией (постстатификацией) выборки.
Малая выборка При большом числе единиц выборочной совокупности (n>100) распределение случайных ошибок выборки по теореме Липунова нормально или приближенно нормально. Расчет ошибки выборки базируется на генеральной дисперсии.
На практике часто приходится сталкиваться с так называемыми малыми выборками. Под малыми выборками подразумевается выборочные наблюдения, численность единиц которых не превышает 30. Разработка теории малой выборки была начата в 1908году английским статистиком В.С. Госсет (Стьюдент). Он доказал, что оценка расхождения между средней малой выборки и генеральной средней имеет особый закон распределения. При оценке результатов малой выборки величина генеральной дисперсии не используется. Для определения пределов ошибки используют критерии Стьюдента.
Чем меньше численность выборки, тем больше распределение Стьюдента отличается от нормального.
Величина t иначе связана с вероятностью, чем при большой выборке. Здесь действует особый закон распределения, и оценка зависит не только от вероятности, но и от объема выборки. Выдержки из таблицы Стьюдента для определения t приведены в таблице №3. Распределение вероятности в малых выборках в зависимости от коэффициента доверия
Пример 7. Предположим, что выборочное обследование 10 рабочих малого предприятия показало, что на выполнение одной из производственных операций рабочие затрачивали времени (мин.): 3,4; 4,7; 1,8; 3,9; 4,2; 3,9; 3,7; 3,2; 2,2; 3,9. Найти предельную величину ошибки для определения среднего с вероятностью 0,924. Найдем выборочные средние затраты:
Выборочная дисперсия
Отсюда средняя ошибка малой выборки
По табл. 3 находим, что для коэффициента доверия
Таблица вероятности Стьюдента чаще приводится и в иной форме, которая считается наиболее удобной для практического использования. Некоторые значения
Число степеней свободы:
Расчет ошибок в малой выборке мало отличается от расчета большой выборки. Расхождение состоит в том, что при малой выборке вероятность наших выводов несколько ниже, чем при большой. Выводы по результатам малой выборки имеют практическое значение лишь при условии, что распределение признаков в генеральной совокупности хотя бы близко к нормальному. Поэтому к малым выборкам прибегают с большой осторожностью. И только в тех случаях, когда проведение большой выборки невозможно.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 874; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |




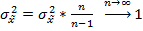



 и объема выборки
и объема выборки 
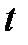
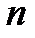

 в таблице даны вероятности нормального распределения. Для определения вероятности соответствующие табличные значения следует разделить на 1000.
в таблице даны вероятности нормального распределения. Для определения вероятности соответствующие табличные значения следует разделить на 1000.
 мин.
мин.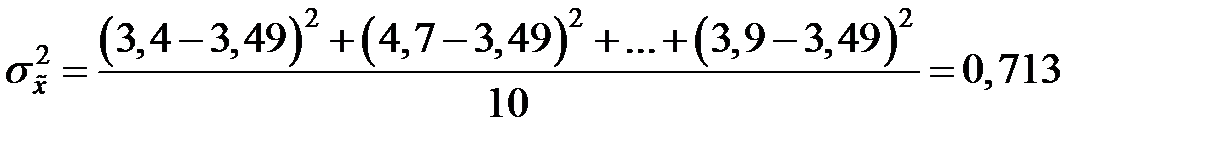
 мин.
мин. объема малой выборки
объема малой выборки 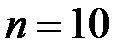 вероятность равна 0,924. Таким образом, с вероятностью 0,924 можно утверждать, что разность
вероятность равна 0,924. Таким образом, с вероятностью 0,924 можно утверждать, что разность  не превысит по абсолютной величине 0,56
не превысит по абсолютной величине 0,56 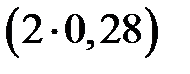 . Следовательно, средние затраты времени во всей совокупности будут находиться в пределах от 2,93 до 4,05 мин. Вероятность того, что это предположение в действительности неверно и ошибка по случайным причинам будет по абсолютной величине больше, чем 0,56, равна:
. Следовательно, средние затраты времени во всей совокупности будут находиться в пределах от 2,93 до 4,05 мин. Вероятность того, что это предположение в действительности неверно и ошибка по случайным причинам будет по абсолютной величине больше, чем 0,56, равна:  .
.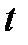 -распределения Стьюдента
-распределения Стьюдента