
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Парная регрессия на основе метода наименьших квадратов (МНК).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одна из проблем при построении уравнения регрессии - это ее размерность. Т.е. определение числа факторных признаков, включаемых в модель. Их количество должно быть оптимальным. С одной стороны, устраняя второстепенные несущественные признаки, и, сокращая размерность, мы получаем модель, которая быстрее и качественнее реализуется. С другой стороны, модель малой размерности может недостаточно полно описывать изучаемое явление. Из практики установлено, что число факторных признаков, включаемых в модель должно быть в 6-7 раз меньше, чем число наблюдений. ПАРНАЯ РЕГРЕССИЯ – это характеристика между двумя признаками: результативным и факторным. Аналитически описывается с помощью следующих уравнений: 1. уравнение прямой 2. гиперболы 3. полинома
Определить, тип уравнения можно исследуя зависимость графически. Существуют и теоретические предпосылки для выбора. Например, если результативный и факторный признак возрастают примерно одинаково в арифметической прогрессии, то связь между ними скорее всего линейная. В случае обратной зависимости может быть гиперболическая. Если факторный признак возрастает в арифметической прогрессии, а результативный значительно быстрее, то может использоваться параболическая или степенная регрессия. Оценка параметров уравнения регрессии осуществляется МНК, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.
Пример. Есть х,у. Ищем ух=а0+а1х. МНК:
МНК создает число уравнений равное числу неизвестных. Также может быть использован для создания функций нескольких переменных. Лекция №11. § 10 РЯДЫ ДИНАМИКИ
Основная цель статистического изучения динамики развития социально-экономических явлений состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики. Ряды динамики – числовые значения определенного стат. показателя в последовательные моменты или периоды времени. В каждом ряду динамики имеются два основных элемента: 1) показатель времени t; 2) соответствующие им уровни развития изучаемого явления у. Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или среднимивеличинами. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки). В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные. Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 1991 г.:
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть персонала магазина, составляющая списочную численность на 1.01 1991 г., продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет. Посредством моментных рядов динамики в торговле изучают товарные запасы, состояние кадров, количество оборудования и других показателей, отображающих состояние изучаемых явлений на отдельные даты (моменты) времени. Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. Примером интервального ряда динамики могут служить данные о розничном товарообороте магазина в 1987-1991 гг.:
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т. д. Свойство суммирования уровней за последовательные интервалы времени позволяет получать ряды динамики более укрупненных периодов. Посредством интервальных рядов динамики в торговле изучается изменение во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования (развития) изучаемых явлений за отдельные периоды. Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов. Ряды динамики формируются в результате сводки и обработки материалов периодического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. При этом каждый ряд динамики охватывает отдельные обособленные периоды, в которых могут происходить изменения, приводящие к несопоставимости отчетных данных с данными других периодов. Поэтому для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду. Для этого в соответствии с задачами исследования устанавливаются причины, обусловившие несопоставимость анализируемой информации, и применяется соответствующая обработка, позволяющая производить сравнение уровней ряда динамики. Для количественной оценки динамики социально-экономических явлений применяются статистические показатели: абсолютные приросты, темпы роста и прироста, темпы наращивания и др. В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения. Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными. Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называются цепными. Все показатели будем вводить и сразу же рассчитывать в таблице примера, который следует далее. Пример: Динамика пр-ва продукции промышленного предприятия за 1985 – 1990 г.г.
Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации. Базисный абсолютный прирост Цепной абсолютный прирост Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень изучаемого периода ниже базисного. В нашем примере в качестве базисного уровня возьмем уровень 1985 года (первого года рассматриваемого периода), т.е.. Тогда, например, для 1988 года:
Между базисными и цепными абсолютными приростамиимеется связь: сумма цепных абсолютных приростов Распространенным статистическим показателем динамики является темп (коэффициент) роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах. Базисные темпы(коэффициенты) роста Цепные темпы(коэффициенты) роста В нашем примере для 1988 года:
Если коэффициент роста больше единицы (или Тр>100%), то это показывает на увеличение изучаемого уровня по сравнению с базисным. Коэффициент роста, равный единице (или Тр=100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Коэффициент роста меньше единицы (или Тр<100%) показывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак. Между базисными и цепными коэффициентами роста имеется взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста, а частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста. Т.е. Темпы (коэффициенты) прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения. Базисный темп (коэффициент) прироста Цепной темп прироста
Между показателями темпа прироста и темпа роста имеется взаимосвязь: Абсолютное значение 1% прироста – это отношение абсолютного прироста к темпу прироста: Средние показатели ряда: Средний уровень ряда динамики характеризует типическую величину абсолютных уровней. В интервальных рядах динамики средний уровень определяется делением суммы уровней на их число: В моментном ряду динамики с равностоящими датами времени средний уровень определяется по формуле средней хронологической:
У нас в примере ряд интервальный, следовательно: Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:
Средний темп роста – обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста применяется формула средней геометрической из показателей коэффициентов роста:
1) 2) Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста для получения средних темпов прироста используется зависимость:
Среднее абсолютное содержание 1% прироста вычисляется делением суммы значений абсолютного содержания 1% прироста на их число:
Графически ряды динамики м.б. представлены в виде линейного графика, диаграммы, структурной диаграммы, картограммы, картосхемы. Приведем пример графика темпов роста.
Лекция №12. §11 КОМПОНЕНТЫ РЯДОВ ДИНАМИКИ При исследовании закономерностей развития социально-экономических явлений, важное значение приобретает изучение общей тенденции развития. Для этого применяются специальные методы анализа в зависимости от конкретики задачи. Изменение уровней рядов динамики обуславливаются влиянием ряда факторов, которые обычно неоднородны по силе, направлению и времени воздействия. Постоянно действующие факторы оказывают определяющее влияние, и формируют в рядах динами основную тенденцию (тренд). Другие факторы действуют периодически. Это вызывает повторяющее во времени колебание уровней. Действия разовых факторов отображается случайными колебаниями. Таким образом, в ряде динамики можно выделить 3 компонента: 1. трендовая (тенденция) 2. периодическая (сезонная) 3. случайная В одних рядах динами основная тенденция проявляется даже при визуальном обзоре исходной информации. В других непосредственно не проявляется, но может быть выражена расчетным путем в виде некоторого теоретического уровня. При изучении основной тенденции решаются 2 взаимосвязанные задачи: 1. выявление наличия тренда и описание его качественных особенностей. 2. измерение выявленного тренда, т.е. получение его количественной характеристики. Основные методы при изучении тренда: 1. метод укрупнения интервалов 2. метод скользящей средней 3. метод серий 4. метод аналитического выравнивания
Метод укрупнения интервалов применяется для выявления тренда в рядах динами колеблющихся уровней, затушевывающих общую тенденцию развития. При этом исходный ряд динамики преобразуется в ряд с более крупными интервалами. Пример. Имеются данные по месячной продажи некоторого товара в магазинах города (штуки).
Вывод: После укрупнения интервалов выявлена тенденция к росту.
При использовании метода скользящей средней по исходным данным определяются теоретические уровни, в которых случайные колебания погашаются, а основная тенденция развития выражается в виде некоторой плавной линии. При использовании метода необходимо установить звенья средней. Они должны состоять из числа уровней отвечающих длительности внутри годовых циклов, в изучаемом явлении. Пример. Рассмотрим применение скользящей средней на данных о реализации некоторой сельхоз продукции в магазинах города.
Т.к. видны колебания длиной в 4 квартала. Используем четырехчленную скользящую среднюю. Вычисление скользящих средних состоит. В определении средних величин из 4 последовательных уровней ряда. При вычислении каждой новой скользящей средней один уровень слева отбрасывается, а один справа добавляется. Результат пишется на середину звена.
При четном числе звеньев дополнительно приходится производить центрирование.
После сглаживания видим, что первые 3 года есть тенденция к росту. С конца 3 года тенденция к снижению. Замечание! Если звено скользящей средней состоит из нечетного числа уровней, центрирование не потребуется. При четном звене центрирование так же можно избежать, если вместо средней арифметической использовать среднюю хронологическую одного уровня.
Метод серий. Каждый конкретный уровень ряда считается принадлежащим к одному из типов: 1. к типу А: 2. к типу В: Последовательность уровней заменяется последовательностью типов, в которой считается число серий R. Серией называется любая последовательность элементов одного типа, ограниченная элементами другого типа. ААВАВВАААВ R=6 Если тенденция в ряде отсутствует, то количество серий является случайной величиной приближенно распределенной по нормальному закону (при n>10), т.е. число серий принадлежить доверительному интервалу.
Среднее число средней
Описанные выше методы позволяют выполнить тренд, но не измерить. Задача измерения средней решается с помощью метода аналитического выравнивания. Суть метода: основная тенденция развития рассчитывается как функция от времени.
Подбирается адекватная математическая функция, которая наилучшим образом отображает тенденцию исследуемого ряда. Подбор функции осуществляется методом наименьших квадратом. MHK: Основная проблема, правильный выбор адекватной математической функции. На практике выделяют следующие эталонные типы:
1. равномерное развитие
В таких рядах используется линейная функция
2. равноускоренное или равнозамедленное развитие
3. развитие с переменным ускорением (замедлением)
4. развития по экспоненте
5. развития с замедлением роста в конце периода
Кроме эталонных применяются и другие математические функции. Если для нахождения параметров линейной функции строится система нормальных уравнений.
На основе модели вычисляются теоретические уровни. Правильность расчетов можно проверить по равенству. Для упрощения расчетов может быть использован способ отсчета от условного нуля. При этом обозначение времени t выбираются таким образом, чтобы Если ряд содержит нечетное число уровней, то уровень, находящийся в середине обозначают нулем, следующие за ним уровни +1,+2,+3… предыдущие -1, -2, -3… Если в ряде четное число уровней, то вверх от середины ставим числа -1,-3,-5 и тд. Вниз 1,3,5 и тд. Тогда формулы для вычисления коэффициентов упрощаются. А0= A1= Пример. По данным о розничном товарообороте региона в 1980 – 1985 гг. нужно произвести анализ основной тенденции развития товарооборота:
Для установления в данном ряду динамики типа развития определяющим признаком является характер изменения абсолютных приростов. Поскольку при среднем абсолютном приросте, равном 1,04 млрд. руб., величина их изменений незначительная (±0,01 млрд. руб.), то анализируемый ряд динамики можно считать с равномерным развитием. Поэтому для аналитического выравнивания применяется функция (1) Для вычисления параметров функции (1) на основе требований метода наименьших квадратов составляется система нормальных уравнений:
Решением системы является:
Используя вычисленные суммы, получаем:
По вычисленным параметрам производим синтезирование трендовой модели функции Правильность расчетов проверяется по равенству: Параметр Используем способ отсчета от условного нуля для рассмотренного выше примера. В нашем случае число уровней четно (6 лет), поэтому в середину ставим +1 и -1, получаем нумерацию с шагом 2. Расчетная таблица имеет вид:
Получаем уравнение Практика статистического изучения тренда социально-экономических явлений показывает, что порой невозможно однозначно решить вопрос, какому типу развития больше всего отвечают показатели ряда динамики. Рассмотренные выше признаки классификации типов развития (абсолютные приросты, темпы роста и прироста) весьма схематичны. На практике ряды динамики с показателями, соответствующими признаками эталонных математических функций, скорее исключение, чем правило. Но, как отмечалось выше, при изучении социально-экономических явлений приходится иметь дело со сложным механизмом взаимодействия факторов, формирующих тренд. Поэтому на основе качественного анализа не всегда возможно получать надежные выводы о типе развития в виде адекватной математической функции. В лучшем случае на основе качественного анализа может быть выдвинута рабочая гипотеза о возможных типах развития. Но выбор на этой основе конкретной математической функции весьма затруднителен. Особенно это относится к криволинейным функциям, теория которых разработана недостаточно: Для подтверждения гипотезы о возможном типе развития можно использовать графический метод. Наглядное изображение анализируемого ряда динамики позволяет получать образное представление о размещении на поле графика эмпирических уровней. Это способствует лучшему осмыслению специфики изменений в ряду динамики. Но дать обобщенную статистическую оценку выявленного тренда графический метод не может. Одним из применяемых в практике статистического изучения тренда показателей адекватности математической функции является стандартизованная ошибка аппроксимации
или средняя ошибка аппроксимации
Лекция № 13. §12 Индексный метод в статистике
СТАТИСТИЧЕСКИЙ ИНДЕКС – это относительная величина сравнения сложных совокупностей и их отдельных единиц. Под сложной понимается совокупность, отдельные единицы, которые не подлежат непосредственному суммированию. При этом в сложных статистических совокупностях единицами наблюдения являются товары с различными потребительскими свойствами. Поэтому для получения обобщающих величин прибегают к индексному методу. Основа метода: При определении изменений в производстве и обращении товаров осуществляется переход от натурально вещественной формы измерения товарных масс к стоимостным (денежным) измерительным. Таким образом, устраняется несравнимость таких товаров как потребительных стоимостей и достигается единство. Экономическое содержание индексов: Они характеризуют изменения индексируемого показателя в отчетном периоде по сравнению с базисным; изменение явления в пространстве или в динамике, т.е. за ряд лет. Задачи индексного метода: 1. характеристика общего изменения сложного экономического явления. 2. выделение в показатели изменения сложного явления влияния одного из факторов путем абстрагирования от влияния других факторов.
Каждая величина, изменение которой изучается называется индексируемой и имеет свое обозначение. p – цена единицы, изделия или товара z – себестоимость единицы продукции t – трудоемкость единицы продукции качественные показатели w – производительность труда или выработка ( q – объем произведенной или реализованной продукции в натуральном выражении (количественный показатель)
Q = p*q – выручка или товарооборот z*q – общие денежные затраты на производство t*q – трудовые затраты
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 884; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.3 (0.011 с.) |






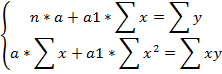

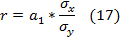
 исчисляется как разность между сравниваемым уровнем
исчисляется как разность между сравниваемым уровнем 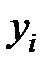 ; и уровнем, принятым за постоянную базу сравнения
; и уровнем, принятым за постоянную базу сравнения  :
:  .
. — разность между сравниваемым уровнем
— разность между сравниваемым уровнем  и уровнем, который ему предшествует,
и уровнем, который ему предшествует,  :
:  .
. ,
, 
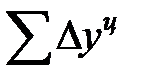 равна базисному абсолютному приросту последнего периода ряда динамики
равна базисному абсолютному приросту последнего периода ряда динамики 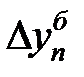 :
:  . У нас
. У нас  и
и 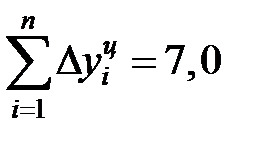 .
. исчисляются делением сравниваемого уровня на уровень, принятый за постоянную базу сравнения,
исчисляются делением сравниваемого уровня на уровень, принятый за постоянную базу сравнения,  :
:  ;
;  .
. исчисляются делением сравниваемого уровня
исчисляются делением сравниваемого уровня  на предыдущий уровень
на предыдущий уровень 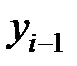 :
:  ;
; 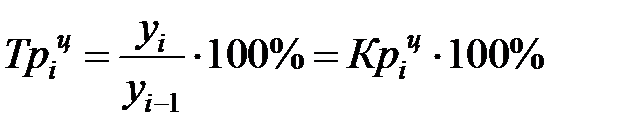 .
. , тогда
, тогда  ,
,  , тогда
, тогда 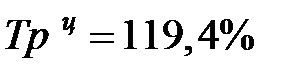
 . У нас
. У нас 
 вычисляется делением сравниваемого базисного абсолютного прироста на уровень, принятый за постоянную базу сравнения.
вычисляется делением сравниваемого базисного абсолютного прироста на уровень, принятый за постоянную базу сравнения. – это отношение сравниваемого цепного абсолютного прироста к предыдущему уровню:
– это отношение сравниваемого цепного абсолютного прироста к предыдущему уровню: или
или 
 или
или  . Последние две формулы дают 2-й способ вычисления темпа прироста.
. Последние две формулы дают 2-й способ вычисления темпа прироста. или (2-й способ)
или (2-й способ)  .
. .
.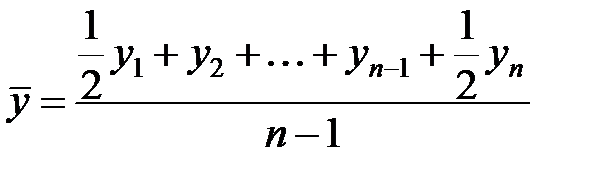
 , т.е. среднегодовое производство продукции составило 21,17 млн.р.
, т.е. среднегодовое производство продукции составило 21,17 млн.р. .
. , т.е. в среднем за год производство продукции увеличивалось на 1,4 млн руб.
, т.е. в среднем за год производство продукции увеличивалось на 1,4 млн руб. ,
,  где
где  – число темпов роста, или
– число темпов роста, или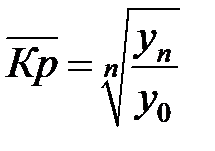 ,
,  , где
, где 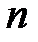 – число уровней ряда, уменьшенное на 1.
– число уровней ряда, уменьшенное на 1. , т.е. в среднем за год производство продукции увеличивалось в 1,068 раза.
, т.е. в среднем за год производство продукции увеличивалось в 1,068 раза. .
. ,
,  (при выражении среднего темпа роста в процентах).
(при выражении среднего темпа роста в процентах). , т.е. в среднем за год производство продукции увеличивалось на 6,8 %.
, т.е. в среднем за год производство продукции увеличивалось на 6,8 %. .
.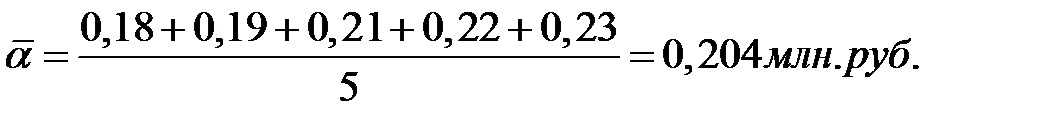 , т.е. на каждый процент прироста приходится 204 тыс. руб.
, т.е. на каждый процент прироста приходится 204 тыс. руб.


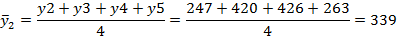



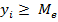

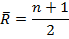






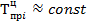





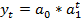

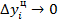
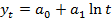



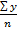


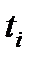



 .
. .
. ,
, 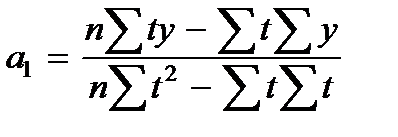 .
. млрд. руб.,
млрд. руб., млрд. руб.
млрд. руб.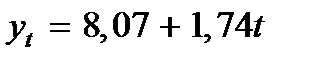 . На основе модели определяются теоретические уровни тренда
. На основе модели определяются теоретические уровни тренда 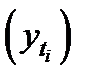 для каждого года анализируемого ряда динамики (графа 8 в табл.).
для каждого года анализируемого ряда динамики (графа 8 в табл.). . Несовпадение в равенстве объясняется округлениями в расчетах.
. Несовпадение в равенстве объясняется округлениями в расчетах.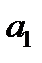 трендовой модели показывает, что объем розничного товарооборота региона возрастал в среднем на 1,74 млрд. руб. в год.
трендовой модели показывает, что объем розничного товарооборота региона возрастал в среднем на 1,74 млрд. руб. в год.




 ,
,  .
. . У нас шаг при нумерации лет составлял
. У нас шаг при нумерации лет составлял 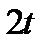 , т.е. увеличение
, т.е. увеличение  на единицу соответствует полугоду. Таким образом, коэффициент регрессии
на единицу соответствует полугоду. Таким образом, коэффициент регрессии  говорит о том, что объем розничного товарооборота региона возрастал в среднем на 0,87 млрд. руб. за полгода, что соответствует ранее выявленному приросту на 1,74 млрд. руб. в год.
говорит о том, что объем розничного товарооборота региона возрастал в среднем на 0,87 млрд. руб. за полгода, что соответствует ранее выявленному приросту на 1,74 млрд. руб. в год.
 .
.



