Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Регрессионный и дисперсионный анализ.Содержание книги
Поиск на нашем сайте
http://ami.nstu.ru/~headrd/seminar/Dis_refr.htm В классических регрессионном и дисперсионном анализах аппарат проверки статистических гипотез базируется на предположении нормальности закона ошибок наблюдений. Нарушение данного предположения по-разному отражается на распределениях статистик используемых критериев проверки гипотез. Предельные распределения статистик критериев могут зависеть от закона распределения ошибок и применяемого метода оценивания параметров. В данной работе исследуются распределения статистик, используемых при проверке гипотез в линейном регрессионном и дисперсионном анализах, при различных отклонениях закона распределения ошибок от нормального. В качестве возможных законов распределений ошибок рассматриваются распределения: логистическое с плотностью Рассматриваемая модель отклика имеет вид где В самом общем виде линейную гипотезу относительно параметров можно представить следующим образом где где где плотность бета-распределения задается выражением [3] Исследование распределений статистики вида (3) в случае отклонения распределения ошибок наблюдений от нормального проводилось с помощью хорошо зарекомендовавшей себя [4, 5] методики компьютерного моделирования. Методика предусматривает моделирование выборок значений исследуемых статистик и сглаживание полученных выборок наиболее подходящим теоретическим распределением. Для более точного определения модели (предельного) распределения статистики параметры аппроксимирующего закона усредняются по множеству экспериментов (по серии смоделированных выборок статистики).
Рассмотрим некоторые результаты исследований, полученные в рамках регрессионного и дисперсионного анализов. Простейшей гипотезой, рассматриваемой в регрессионном анализе, является гипотеза об адекватности оценок вектора неизвестных параметров а статистика (3) значительно упрощается и принимает вид (учитывая, что в регрессионном анализе В [1] показано, что в случае нормального закона распределения отклонений регрессии Проведенные исследования показали, что в большинстве рассмотренных нами случаев эмпирические функции распределения статистики (6), полученные в результате моделирования, при использовании для оценивания вектора параметров регрессии метода максимального правдоподобия хорошо описываются бета-распределением II рода. Для различных значений числа наблюдений n и количества m оцениваемых параметров линейной регрессии найдены значения параметров бета-распределения II рода, аппроксимирующего в соответствующем случае распределение статистики (6). Найденные аппроксимации могут выступать при проверке гипотез в качестве моделей предельных распределений статистик в случае ошибок наблюдений отклика, подчиняющихся законам распределения Коши и экспоненциальному семейству с параметрами формы l=0.5, l=1.0 (соответствует распределению Лапласа), l=2.0 (соответствует нормальному закону), l=3.0, l=10.0. В случае логистического закона ошибок наблюдений в качестве предельного распределения статистики (6), как и в «классическом» случае, может использоваться распределение Фишера
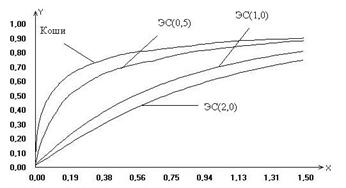
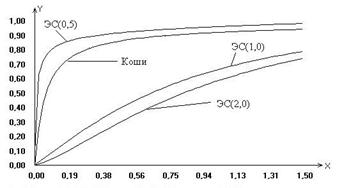
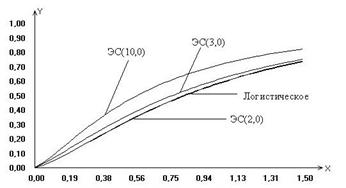
Рис. 1 Рис. 2 На рисунках 1 и 2 в качестве иллюстрации представлены построенные в результате исследований модели предельных распределений статистики (6), соответствующие различным законам распределения ошибок наблюдений. Рассматривая полученные модели распределений статистик, можно сделать вывод, что незначительные отклонения закона распределения ошибок наблюдений отклика от нормального (как в случае логистического закона распределения) не влияют значимо на предельное распределение исследуемой статистики. В то же время для моделей регрессии с ошибками наблюдений, подчиняющимися законам распределения, сильно отличающимся по свойствам от нормального (Коши, ЭС при Для того чтобы можно было сравнить результаты исследований задач дисперсионного анализа с результатами, приведенными выше для регрессионного анализа, была рассмотрена нетипичная для дисперсионного анализа модель с невырожденной матрицей В этом случае На рис. 3-4 приведены построенные приближения предельных законов распределений статистики (3) для проверки гипотезы вида (5) на примере модели (7) в случаях, когда закон распределения ошибок наблюдения описывается распределением Коши, логистическим или экспоненциальным семейством с различными параметрами формы Вид функций распределения статистики (3), представленных на рис. 4, показывает, что при увеличении параметра формы распределения экспоненциального семейства ошибок наблюдения приближенные предельные распределения статистик также, “поднимаясь”, удаляются, хотя, может быть, и не с такой скоростью как в случае уменьшения параметра формы, от предельного распределения статистики, соответствующего случаю нормального распределения ошибок. Представленный здесь также случай логистического распределения ошибок наблюдения, которое интересно тем, что по своим свойствам очень близко к нормальному, позволяет сделать вывод о том, что если распределения ошибок наблюдения близко к нормальному, то и предельное распределение статистики будет близко к классическому F -распределению Фишера.
Рис. 3 Рис. 4
В целом, сравнивая результаты исследований на регрессионных и дисперсионных моделях вида (7), которые проводились независимо, можно отметить схожее поведение распределений статистик. Существенные различия были заметны в поведении предельного распределения статистики в случае распределения ошибок наблюдений, подчиняющихся закону Коши, по отношению к поведению предельного распределения статистики в случае ошибок наблюдений, распределенных в соответствии экспоненциальным семейством при l Далее была предпринята попытка выяснить, будут ли результаты, приводимые выше, различаться с результатами, которые могут быть получены для классической модели дисперсионного анализа – модели с вырожденной матрицей которая отличается от модели (7) тем, что в векторе параметров появляется еще один элемент – аддитивная постоянная
где В целом сравнение результатов, полученных в рамках регрессионного и дисперсионного анализа для моделей, в которых ошибка наблюдений подчиняется двустороннему экспоненциальному закону распределения с различными значениями параметра формы, позволило выявить общие тенденции. Полученное в результате моделирования приближение предельного распределения статистики (3) при параметре формы двустороннего экспоненциального закона l = 2 совпадает с предельной функцией распределения статистики для “классического” случая. В данном случае при проверке согласия получаемых в результате моделирования эмпирических распределений статистик с предельным “классическим” F -распределением Фишера всегда достигался очень высокий уровень значимости по всем применяемым критериям согласия [9,10]. Самое “высокое” (на рисунках) из рассмотренных приближений предельных функций распределения статистик получается при значении параметра l=0,5 (из рассмотренных). Далее с ростом значения параметра l вплоть до l = 2, приближенные функции распределения “спускаются” к предельному закону, справедливому для “классической” регрессии. При дальнейшем росте значения параметра формы, приближенные функции распределения статистики “поднимаются” от предельного закона, справедливого для статистики критерия при нормальных ошибках наблюдений.
Рис. 5 Рис. 6
Проведенные исследования показали перспективность применения методики компьютерного исследования статистических закономерностей в задачах регрессионного и дисперсионного анализа. Исследования показали возможность построения простых аналитических моделей для распределений статистик, используемых при проверке статистических гипотез в регрессионном и дисперсионном анализе. Часто хорошей моделью для распределений статистик, используемых в регрессионном и дисперсионном анализах, оказывается бета-распределение II-го рода. Построены модели распределений статистик для ряда законов распределений ошибок отклика при различных регрессионных моделях.
Применение методов дисперсионного и регрессионного анализа позволяет не только оценить существенность влияния различных факторов на свойства машины, но и в ряде случаев устанавливать аналитические зависимости между учитываемыми факторами и признаками, характеризующими те или иные свойства машины. [ 1 ]
Каковы условия для изменения дисперсионного и регрессионного анализа, которым должны удовлетворять ВПО. [ 2 ] Распространенными (эффективными) для подобных задач считаются методы дисперсионного и регрессионного анализа, а также методы анализа данных. [ 3 ] Результаты экспериментов по определению коррозионной стойкости низколегированной стали, полученные согласно построенным планам комплексных исследований, обрабатывались методами корреляционного, дисперсионного и регрессионного анализа, что позволило создать модели для численного прогнозирования коррозионных процессов. [ 4 ] Значительные изменения в методике исследования технологических процессов произошли с развитием и внедрением идей планирования эксперимента, где подразумевается использование и тесное взаимодействие дисперсионного и регрессионного анализа. [ 5 ] К первому виду обработки относится определение статистических характеристик по результатам испытаний, нахождение погрешности и ошибок измерения, аппроксимирующее сглаживание и экстраполяция экспериментальных кривых, дисперсионный и регрессионный анализ, определение общего вида расчетных аналитических зависимостей, построение графиков и номограмм. [ 6 ] В процессе отработки методики на лабораторном стенде было установлено, что асфальтосмолопарафиновые отложения (АСПО) не образуются за время эксперимента (24 ч) и поэтому не вносят погрешность в результаты измерений. Обработку данных производили с использованием методов корреляционного, дисперсионного и регрессионного анализа, что позволило дать сравнительный анализ процессов образования гидратов железа или его окислов в околотрубном пространстве нефтяных скважин. [ 7 ]
В этом случае ЭВМ оценивает параметры распределений случайных величин, подбирает их законы распределения, выполняет дисперсионный и регрессионный анализ. Результаты испытаний могут непосредственно вводиться с испытательной установки (ИУ) в ЭВМ через устройство связи с объектом испытаний (УСО), или их предварительно обрабатывают вручную и затем вводят в ЭВМ в виде массивов данных. В математическом обеспечении ЭВМ должны быть стандартные программы обработки экспериментальных результатов. [ 8 ] В ряде случаев, например, при установлении нормативов на обслуживание и ремонт машин, необходимо знать значения характеристик ремонтопригодности для конкретных условий их использования, обслуживания и ремонта. Существенность влияния факторов, определяющих эти условия, может быть оценена планированием экспериментов и анализом их результатов с использованием методов дисперсионного и регрессионного анализа, рассмотренных в гл. Для этой цели могут быть использованы и методы проверки статистических гипотез о равенстве (различии) числовых характеристик двух или более групп наблюдений показателя ремонтопригодности, проведенных при различных уровнях (условиях) интересующего фактора. Примеры применения этих методов рассматриваются в гл. [ 9 ] Задачи (17) - (21) относятся к исследованию моделей, в которых на выходные технические характеристики влияет ряд факторов и необходимо выявить их наиболее неблагоприятное (или, наоборот, оптимальное) сочетание, а также степень влияния. Сюда же относятся испытания при предельных и повышенных нагрузках, а также некоторые специальные виды испытаний - вверх - вниз и др. В этих задачах используются дисперсионный, регрессионный анализ, факторный эксперимент. [ 10 ] В настоящее время под влиянием практических потребностей эти направления математической статистики в достаточной мере обеспечены литературой, отражающей как теоретические, так и прикладные аспекты их развития. Постановка задач в этой области и полезные литературные ссылки имеются в книгах Уилкса (1967), гл. Наиболее полно дисперсионный и регрессионный анализ изложен в монографиях Шеффе (1963), Плэкета (1960) и Уильямса (1959); широко обсуждаются вопросы оптимального планирования экспериментов, которое имеет целью увеличение точности статистических оценок; при регрессионном анализе, например, задача планирования состоит в указании таких значений контролируемых переменных, при которых некая заданная функция от неизвестных параметров обладает теми или иными экстремальными свойствами. Подробный анализ темы планирования, посвященный практическим задачам регрессионного и конфлюэнтного анализа, имеется в работе Клепикова и Соколова (1964) ср. [ 11 ] Надежная статистическая оценка вклада контролируемых факторов возможна лишь при условии, что эксперимент (наблюдение) некоторым образом организован. Это определяет тесную связь дисперсионного анализа с планированием эксперимента. В тех случаях, когда изменение хотя бы части контролируемых факторов может быть измерено количественно, пользуются комбинацией дисперсионного и регрессионного анализа (см. гл. [ 12 ] - Метод семи инструментов. Другие названия метода: "Семь новых инструментов контроля качества", "Семь инструментов планирования и управления". Автор метода: Японский союз ученых и инженеров, 1979 г. Назначение метода Наиболее часто эти инструменты находят применение при решении проблем, возникающих на этапе проектирования. Цель метода Решение проблем, возникающих в процессе организации, планирования и управления бизнесом на основе анализа различного рода фактов. Суть метода Семь инструментов управления качеством (УК) обеспечивают понимание сложных ситуаций и позволяют облегчить задачу управления качеством путем улучшения процесса проектирования продукции или услуги. Инструменты УК усиливают процесс планирования благодаря их способности: уяснять задачи; устранять недостатки; содействовать распространению и обмену информацией между заинтересованными сторонами; использовать бытовую лексику. В результате инструменты УК позволяют вырабатывать оптимальные решения в кратчайшие сроки. Диаграмма сродства и диаграмма связей обеспечивает общее планирование. Диаграмма дерева, матричная диаграмма и матрица приоритетов обеспечивает промежуточное планирование. Блок-схема процесса принятия решения и стрелочная диаграмма обеспечивает детальное планирование. План действий Последовательность применения методов может быть различной в зависимости от поставленной цели. Эти методы можно рассматривать и как отдельные инструменты, и как систему методов. Каждый метод может находить свое самостоятельное применение в зависимости от того, к какому классу относится задача. Особенности метода Семь инструментов управления качеством - набор инструментов, позволяющих облегчить задачу управления качеством в процессе организации, планирования и управления бизнесом при анализе различного рода фактов. Диаграмма сродства - инструмент, позволяющий выявлять основные нарушения процесса путем обобщения и анализа близких устных данных. Диаграмма связей - инструмент, позволяющий выявлять логические связи между основной идеей, проблемой и различными факторами влияния. Диаграмма дерева - инструмент стимулирования процесса творческого мышления, способствующий систематическому поиску наиболее подходящих и эффективных средств решения проблем. Матричная диаграмма - инструмент, позволяющий выявлять важность различных неочевидных (скрытых) связей. Обычно используются двумерные матрицы в виде таблиц со строками и столбцами a1, a2,., b1, b2. - компоненты исследуемых объектов. Матрица приоритетов - инструмент, для обработки большого количества числовых данных, полученных при построении матричных диаграмм, с целью выявления приоритетных данных. Этот анализ часто рассматривается как факультативный. Блок-схема процесса принятия решения - это инструмент, который помогает запустить механизм непрерывного планирования. Его использование способствует уменьшению риска практически в любом деле. Планирует каждый мыслимый случай, который может произойти, перемещаясь от утверждения проблемы до возможных решений. Стрелочная диаграмма - инструмент, позволяющий планировать оптимальные сроки выполнения всех необходимых работ для реализации поставленной цели и эффективно их контролировать. Дополнительная информация: Семь инструментов УК обеспечивают средства для понимания сложных ситуаций и соответствующего планирования, формируют согласие и ведут к успеху при коллективном решении проблем. Шесть из этих инструментов используются в работе не с конкретными числовыми данными, а со словесными высказываниями и требуют понимания концепций семантики для обнаружения и сбора основных данных. Сбор исходных данных обычно осуществляют во время "мозговых атак". Достоинства метода Наглядность, простота освоения и применения. Недостатки метода Низкая эффективность при проведении анализа сложных процессов. Ожидаемый результат Использование инструментов управления качеством позволяет экономить ресурсы и тем самым улучшает чистую прибыль компании. А.М. Кузьмин "Метод "Семь инструментов управления качеством"" и другие Методы поиска идей и создания инноваций - Блок-схема процесса. Блок-схема процесса Блок-схема - это схематическое представление этапов выполнения любого процесса; порядок, в котором следуют отдельные операции, с использованием специальных символов, отражающих природу этих операций, как это показано на рисунке 1.1. Процесс создания и анализа блок-схемы позволяет выявить источник проблемы.
Рис. 1.1. Символы, используемые на блок-схемах (Источник: В5 7850: часть 2:1992): 1 - описание документа, 2 - начало и конец этапа,3 - описание деятельности, 4 - принятие решения, 5 -указание направления потока от одного этапа работы к другому, 6 - описание базы данных. Пример построения блок-схемы разработки документа.
Рис. 1.2. Блок - схема (для разработки документа) (Источник: 35 7850: Часть 2:1992) Контрольное задание № 1 Разработать блок-схему для цикла совершенствования процесса и ид Блок-схема - это графическое отображение процесса, которое четко показывает нам, как протекает процесс. Блок-схема показывает систематическую последовательность этапов выполнения работы и то, какие группы вовлечены в процесс.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.84.128 (0.013 с.) |

 , Коши с плотностью
, Коши с плотностью  , экспоненциальное семейство (ЭС) распределений с плотностью
, экспоненциальное семейство (ЭС) распределений с плотностью 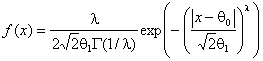 при различных значениях параметра формы
при различных значениях параметра формы 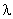 .
.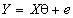 , (1)
, (1)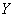 – вектор наблюдений размерности
– вектор наблюдений размерности  ,
, 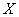 – матрица независимых переменных размерности (
– матрица независимых переменных размерности ( 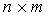 ), отражающая структуру проводимых экспериментов,
), отражающая структуру проводимых экспериментов, 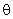 – вектор оцениваемых параметров размерности
– вектор оцениваемых параметров размерности 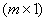 ,
, 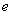 – вектор ошибок наблюдения системы размерности (
– вектор ошибок наблюдения системы размерности ( 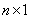 ). В регрессионном анализе матрица
). В регрессионном анализе матрица 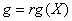 – ранг матрицы
– ранг матрицы 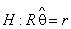 , (2)
, (2)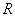 - известная матрица
- известная матрица 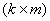 ,
, 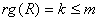 ;
; 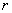 - заданный вектор
- заданный вектор  ,
,  - оценка вектора параметров
- оценка вектора параметров  , (3)
, (3) – матрица, обобщенно-обратная к
– матрица, обобщенно-обратная к  , совпадающая с матрицей
, совпадающая с матрицей  в случае, если
в случае, если  является матрица полного ранга, т.е.
является матрица полного ранга, т.е.  . В [1, 2] показано, что в случае нормальности ошибок наблюдений, статистика (3) подчиняется закону распределения Фишера
. В [1, 2] показано, что в случае нормальности ошибок наблюдений, статистика (3) подчиняется закону распределения Фишера 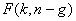 со степенями свободы k и n-g. Отметим, что распределение Фишера является частным случаем бета-распределения II рода:
со степенями свободы k и n-g. Отметим, что распределение Фишера является частным случаем бета-распределения II рода: , (4)
, (4)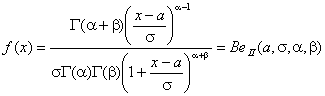 .
.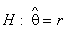 , (5)
, (5) . (6)
. (6)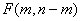 .
.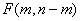 .
.
 и т.п.), распределения статистики (6) также сильно отличаются от «классического» предельного распределения
и т.п.), распределения статистики (6) также сильно отличаются от «классического» предельного распределения 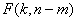 .
.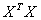 , которая допускает проверку гипотезы, аналогичной по форме гипотезе (5). Матрица
, которая допускает проверку гипотезы, аналогичной по форме гипотезе (5). Матрица 
 (7)
(7) ,
,  ,
,  ,
, 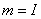 . При проведении исследований использовалась модель вида (7) размерности
. При проведении исследований использовалась модель вида (7) размерности 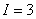 , имеющая ранг матрицы планирования
, имеющая ранг матрицы планирования 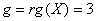 ,
, 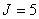 ,
, 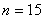 . При всех перечисленных характеристиках модели (7) распределение статистики (3) для проверки гипотезы вида (5) в случае нормально распределенной ошибки наблюдений будет подчиняться распределению Фишера
. При всех перечисленных характеристиках модели (7) распределение статистики (3) для проверки гипотезы вида (5) в случае нормально распределенной ошибки наблюдений будет подчиняться распределению Фишера  .
.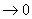 . Распределение статистики (3) при ошибках, подчиняющихся распределению Коши, является, как это можно увидеть по рис. 3, некоторым пределом распределений статистик для моделей, с ошибками наблюдений, подчиняющимися распределениям экспоненциального семейства при l
. Распределение статистики (3) при ошибках, подчиняющихся распределению Коши, является, как это можно увидеть по рис. 3, некоторым пределом распределений статистик для моделей, с ошибками наблюдений, подчиняющимися распределениям экспоненциального семейства при l 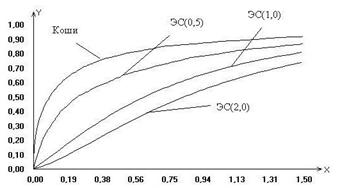

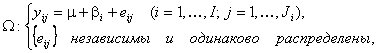 (8)
(8)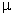 , а в матрице планирования
, а в матрице планирования 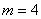 ,
, 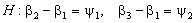 , (9)
, (9) и
и  - некоторые известные значения ФДО
- некоторые известные значения ФДО 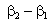 и
и  . При проверке этой гипотезы распределение статистики (3) в случае нормально распределенной ошибки наблюдений будет подчиняться закону распределения Фишера
. При проверке этой гипотезы распределение статистики (3) в случае нормально распределенной ошибки наблюдений будет подчиняться закону распределения Фишера  . На рис. 5 и рис. 6 приведены данные, полученные для модели (8) при проверке гипотезы (9), аналогичные тем, что были приведены на рис. 3 и рис. 4 для модели (7) при проверке гипотезы (5). Сравнительный анализ рис. 3 и рис. 5, рис. 4 и рис. 6 позволяет говорить о том, что вырожденность матрицы
. На рис. 5 и рис. 6 приведены данные, полученные для модели (8) при проверке гипотезы (9), аналогичные тем, что были приведены на рис. 3 и рис. 4 для модели (7) при проверке гипотезы (5). Сравнительный анализ рис. 3 и рис. 5, рис. 4 и рис. 6 позволяет говорить о том, что вырожденность матрицы