Стреловидные диаграммы (сетевой график).

Сетевой график – это инструмент качества, предназначенный для планирования и управления работами. Изначально, в составе семи новых инструментов управления качеством применялась стрелочная диаграмма, но для практического применения более часто используют сетевой график или диаграмму Ганта.

Все это разные инструменты (хотя часто в литературе и Интернете можно встретить, что это один и тот же инструмент с разными названиями), у каждого из которых есть свои достоинства и недостатки, однако все они служат одной цели – планированию и управлению работами.

Наиболее часто сетевой график применяется для проектов или различных работ, которые составляют набор взаимосвязанных действий. Его применение позволяет определить сроки завершения проекта и выявить возможные варианты сокращения сроков работ. Т.к. работы в сетевом графике взаимоувязаны по времени, то это дает возможность осуществлять контроль хода работ.

По своей сути сетевой график является графом, вершины которого представляют события (состояние работы или объекта в некоторый момент времени), а соединяющие вершины ребра (дуги графа) отображают работы. Сетевой график, представленный в таком виде, является частью метода PERT (Program Evaluation and Review Technique), разработанного в 1957-58 годах одной из американских компаний для планирования и оценки хода работ проекта.

Существует и другой вариант представления сетевого графика, когда вершинами графа являются работы, а дуги показывают только взаимосвязь между ними. Такой вариант используется чаще. Он является частью метода CPM (Critical Path Method – метод критического пути).

Порядок построения сетевого графика по методу критического пути следующий:

1. Определяется основная цель планирования – результат, который должен быть получен по завершении работ. Это дает возможность определить границы проекта и примерные сроки завершения работ.

2. Выявляются ограничения, влияющие на сетевой график и планируемые действия. Такими ограничениями обычно являются какие-либо внешние условия, время и стоимость.

3. Определяется состав задач (действий) необходимых для достижения поставленной цели. Состав задач можно выявить с помощью древовидной диаграммы (в этом случае сетевой график будет представлять только задачи верхних уровней древовидной диаграммы). Задачи указываются на отдельных карточках или стикерах.

4. На карточках, для каждой задачи отмечается длительность ее выполнения. Можно указать ресурсы, инструменты и ответственных за выполнение задачи. Длительность необходимо указывать в одних и тех же единицах измерения для всех задач (например, в минутах, часах, днях и т.д.). В противном случае составить сетевой график будет проблематично. Длительность задач должна быть величиной одного порядка. Например, если большинство задач выполняется за несколько часов, а одна за две-три недели, то это означает, что такая задача должна быть детализирована на составляющие.

5. Рассматриваются все задачи, и определяется, какая из них должна быть выполнена первой. Карточка с этой задачей располагается на сетевом графике слева, либо сверху. Если таких задач больше чем одна, то карточки располагаются одна над другой (одна рядом с другой).

6. Определяется задача, которая должна быть выполнена сразу же после первой. Карточка с этой задачей располагается справа от первой карточки (либо снизу, если выбран вертикальный вариант расположения задач). Если должны начинаться две и более задач, то карточки располагаются одна над другой (одня рядом с другой). Далее определяется задача, которая должна начинаться сразу же после второй, и так далее, пока все карточки с задачами не окажутся расположенными в цепочку.

Если задача должна начинаться до завершения предыдущей задачи, то предыдущую задачу необходимо разделить на составляющие. Задачи могут выполняться параллельно, но при условии, что связь задач точно определена. Начало выполнения параллельных задач должно быть строго привязано к завершению предыдущей задачи (задач).

7. Отображаются связи между задачами – обычно в виде стрелок, которые показывают последовательность выполнения задач. Направление стрелок устанавливается слева направо (сверху вниз). Для того чтобы между карточками с задачами можно было прорисовать связи, карточки необходимо закрепить на какой-либо ровной поверхности.

Сейчас сетевой график, конечно, наиболее удобно строить, используя программные средства, например MS Visio.

8. Определяется раннее начало и раннее окончание каждой задачи. Для этого сетевой график просматривают в прямом направлении - начинают с первой задачи и далее по очереди двигаются к последней. При этом необходимо соблюдать правило - последующая задача не может быть начата, пока не завершены все предшествующие задачи. Раннее начало последующей задачи будет совпадать с ранним завершением предшествующей. Если предшествующих задач несколько, то ранним началом последующей задачи будет наибольшее из значений раннего окончания одной из предшествующих задач. Ранее окончание каждой из задач определяется как раннее начало плюс длительность задачи.

9. Определяется позднее начало и позднее окончание каждой задачи. Для этого сетевой график просматривают в обратном направлении - начинают с последней задачи и далее по очереди двигаются к первой. При этом необходимо соблюдать правило – предшествующая задача должна быть завершена до того, как начнется каждая из последующих задач. Позднее окончание задачи будет совпадать с поздним началом последующей задачи. Если последующих задач несколько, то поздним окончанием задачи будет наименьшее из значений позднего начала последующих задач. Позднее начало каждой задачи определяется как позднее окончание минус длительность задачи.

10. Определяется резерв времени для каждой задачи. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием задачи.

11. Определяется путь, где резерв времени для каждой задачи равен нулю. Этот путь называется критическим путем.

Если необходимо оптимизировать сетевой график, то в первую очередь проводится анализ задач, лежащих на критическом пути.

 

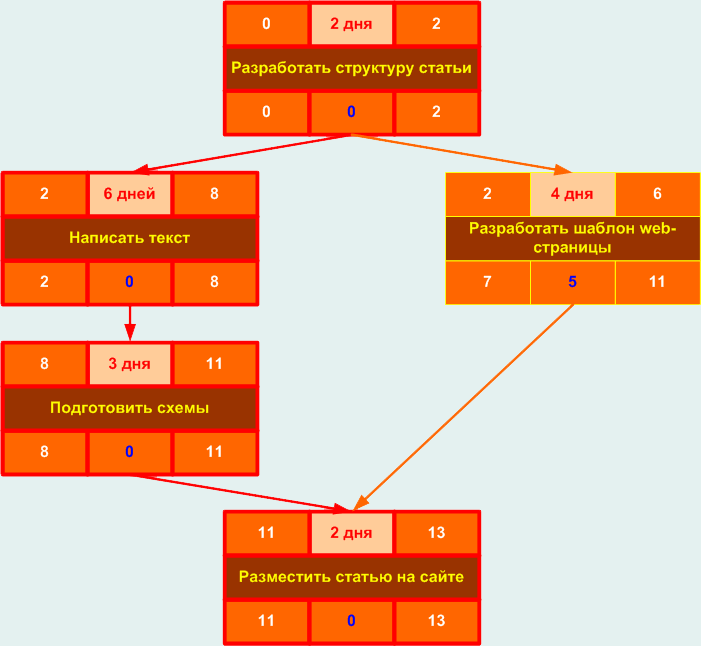
ПРИМЕР

В качестве примера сетевого графика рассматривается написание статьи на сайт. Нумерация действий в примере соответствует порядку шагов построения сетевого графика, указанному выше.

1. Определяем цель планирования - подготовить информационную статью для сайта. Требуемый результат - статья размещена на сайте.

2. Определяем ограничения, влияющие на сетевой график: срок подготовки статьи - не более 15 дней.

3. Определяем состав задач: предполагаем, что весь проект состоит из 5-ти задач.

4. Определяем длительность задач: указываем на карточках в графе "длительность" продолжительность выполнения каждой задачи. Длительность задач может определяться нормативами, либо на основании экспертной оценки.

5. Определяем первую задачу: первая задача, с которой начинается проект – «Разработать структуру статьи». Помещаем эту задачу сверху.

6. Определяем порядок следования оставшихся задач: Располагаем задачи в логической последовательности по порядку их исполнения. При этом проверяем условие, при котором каждая последующая задача не может начаться пока не завершены все предыдущие задачи.

7. Устанавливаем связи между задачами.

8. Определяем раннее начало и раннее окончание каждой задачи: Устанавливаем раннее начало задачи «Разработать структуру статьи» равным нулю, т.к. это первая задача. Раннее окончание рассчитывается как раннее начало плюс длительность задачи, т.е. 0+2=2. Раннее начало задач «Написать текст» и «Разработать шаблон web -страницы» будет равно 2-м, т.к. эти задачи имеют одну предшествующую задачу. Рассчитываем раннее окончание задач «Написать текст» и «Разработать шаблон web -страницы» - получаем 8 и 6 дней соответственно. По аналогии, рассчитываем раннее начало и раннее окончание задачи «Подготовить схемы». Получаем ранее начало - 8 дней, раннее окончание - 11 дней. Задача «Разместить статью на сайте» имеет две предшествующие задачи – «Подготовить схемы» (раннее окончание 11 дней) и «Разработать шаблон web -страницы» (раннее окончание 6 дней). Раннее начало задачи «Разместить статью на сайте» будет совпадать с наибольшим значением раннего окончания предшествующей задачи, т.е. 11 дней. Раннее окончание задачи «Разместить статью на сайте» будет равняться 13 дням. Следовательно, длительность всего проекта составит 13 дней. 9. Определяется позднее начало и позднее окончание каждой задачи. Позднее окончание задачи «Разместить статью на сайте» совпадает с ранним окончанием этой задачи и равняется 13 дням. Позднее начало задачи рассчитывается как позднее окончание минус длительность, и равняется 11 дней. Позднее окончание задач «Подготовить схемы» и «Разработать шаблон web -страницы» будет совпадать с поздним началом задачи «Разместить статью на сайте». Позднее начало этих задач будет равняться 8 дней (для задачи «Подготовить схемы») и 7 дней (для задачи «Разработать шаблон web -страницы»). Рассчитываем позднее окончание и позднее начало задачи «Написать текст». Они составят 8 дней и 2 дня соответственно. Задача «Разработать структуру статьи» имеет две последующие задачи, позднее начало которых составляет 2 дня (задача «Написать текст») и 7 дней (задача «Разработать шаблон web -страницы»). Поэтому позднее окончание задачи «Разработать структуру статьи» составит наименьшее из этих значений, т.е. 2 дня. Позднее начало задачи равняется позднее окончание минус длительность, т.е. 0. 10. Определяем резерв времени для каждой задачи: резерв времени возможен только для задачи «Разработать шаблон web -страницы». Для всех остальных задач резерв времени равен нулю.

11. Определяем критический путь: Критический путь выделен красным цветом. Чтобы сократить длительность проекта необходимо оптимизировать задачи, лежащие на критическом пути.

 

Сетевой график позволяет наглядно представить все задачи проекта, увидеть их взаимосвязь и выявить критические аспекты планируемых работ. Кроме того, важным достоинством сетевого графика является возможность представить влияние той или иной задачи на ход выполнения последующих задач, что важно для контроля работ проекта.

Стрелочная диаграмма [1, 8-10, 41] - инструмент, позволяющий спланировать оптимальные сроки выполнения всех необходимых работ для скорейшего и успешного достижения поставленной цели.

 

Применение этого инструмента рекомендуется после того, когда выявлены проблемы, требующие решения, определены необходимые меры, средства, сроки и этапы их осуществления, т. е. после использования хотя бы одного из рассмотренных выше инструментов:

диаграммы сродства;

диаграммы связей;

древовидной диаграммы;

матричной диаграммы.

 

Стрелочная диаграмма обычно графически представляет ход проведения работ. Из стрелочной диаграммы должны быть наглядно видны порядок и сроки проведения различных этапов работы. Одновременно этот инструмент обеспечивает уверенность, что планируемое время выполнения всей работы и отдельных ее этапов является оптимальным при достижении конечной цели.

 

Стрелочные диаграммы широко применяются не только при планировании работ, но и для последующего контроля их выполнения, в частности, при проектировании и разработке, а также при контроле производственной деятельности.

 

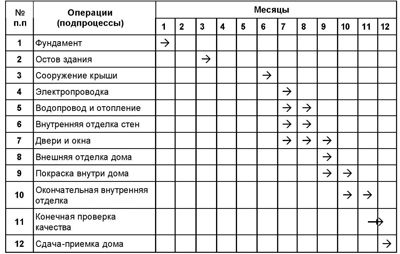
Стрелочные диаграммы чаще всего представляют в виде одной из двух форм — диаграммы Гантта (табл. 4.3) и сетевого графика (рис. 4.8).

 

Сетевой график, часто называемый сетевым графом, выполнения тех же работ по строительству дома приведен на рис. 4.8. Цифры, стоящие в узлах графа,

 

Таблица 4.3

 

Пример диаграммы Гантта для планирования процесса и сроков возведения дома «под ключ» в течение 12 месяцев [1]

соответствуют порядковому номеру работ, приведенных в табл. 4.3. Цифры, размещенные под стрелками сетевого графа, обозначают продолжительность (число месяцев) выполнения конкретных видов работ.

_________ - работа или мероприятие (длина стрелки пропорциональна времени);

-------------- - взаимосвязь между работами, не занимающая времени (показывает, до начала какой работы должна быть завершена предшествующая работа).