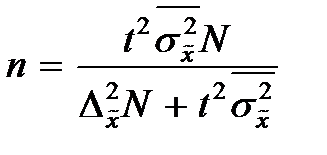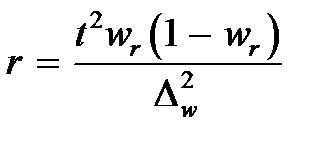Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция №1. Определение предмета статистикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
СТАТИСТИКА Сокольникова Алла Михайловна Литература 1. Статистика: Учебное пособие / Под ред. В. М. Симчеры. М.: 2. Статистика: Учебник / Под ред. И. И. Елисеевой. М.: Высшее образование 3. Теория статистики: Учебник / Под ред. Р. А. Шмойловой. М.: 4. Практикум по теории статистики: Учебное пособие / Под ред. 5. Шимко П. Д. Статистика / П. Д. Шимко, М. П. Власов. Ростов-на-Дону: Феникс 6. Курс социально-экономической статистики: Учебник / Под ред. 7. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учеб. Пособие. – М.: Финансы и статистика Лекция №1. ОПРЕДЕЛЕНИЕ ПРЕДМЕТА СТАТИСТИКИ
Вопрос 1. Определение предмета статистики
Status (лат.) – положение, состояние явлений и процессов. Термин «статистика» употребляется в различных значениях. Под статистикой понимается практическая деятельность по сбору, накоплению, обработке и анализу цифровых данных, характеризующих население, экономику, культуру, образование и другие явления в жизни общества. Статистикой также называют особую науку, т.е. отрасль знаний, изучающую явления в жизни общества с их количественной стороны. Статистика имеет многовековую историю. Ее возникновение и развитие обусловлены общественными потребностями: подсчет населения, скота, учет земельных угодий, имущества и т. д. Наиболее ранние сведения о таких работах в Китае относятся к XXIII в. до нашей эры. В Древнем Риме проводились цензы (учеты) свободных граждан и их имущества. По мере развития общественного производства, внутренней и внешней торговли увеличивалась потребность в статистической информации. Началось формирование статистической науки. Считается, что основы статистической науки заложены английским экономистом У. Петти (1623—1687). Последователи У. Петти образовали научное направление, получившее название «политическая арифметика». Основоположником другого направления развития статистической науки признан немецкий ученый Г. Конринг (1606—1681), который разработал систему описания государственного устройства. Его последователь профессор философии и права Г. Ахенваль (1719—1772) впервые в Марбургском университете (1746 г.) начал читать новую дисциплину, названную им статистикой. Основным содержанием этого курса было описание политического состояния и достопримечательностей государств. Государствоведение нашло отражение и в ряде работ М. В. Ломоносова (1711—1765). Несколько позже профессор Геттингенского университета А. Шлицер (1736 – 1809) опроверг взгляды, что статистика должна лишь описывать политическое устройство государств. Предметом статистики, по А. Шлицеру, является все общество. Дальнейшее развитие статистики осуществлялось многими учеными и практиками. Среди них следует отметить бельгийского статистика А. Кетле (1796 – 1874), внесшего значительный вклад в разработку теории устойчивости статистических показателей. Математическое направление в статистике развивалось в работах Ф. Гальтона (1822 – 1911), К. Пирсона (1857—1936), В. Госсета (1876 – 1936), Р. Фишера (1890 – 1962), М. Митчела (1874 – 1948) и др. Так, К. Пирсон внес значительный вклад в разработку теории количественной оценки связи между явлениями. В. Госсет, писавший под псевдонимом Стьюдента, разработал теорию малой выборки. Р. Фишер развивал методы количественного анализа. М. Митчелу принадлежит идея «экономического барометра». Представители этого направления считают основой статистики теорию вероятностей, составляющую одну из отраслей прикладной математики. В развитии статистики видное место принадлежит представителям отечественной науки и практики. В эпоху Петра I в работах И. К. Кирилова (1689 – 737) и В. Н. Татищева (1686 – 1750) статистика трактовалась преимущественно как описательная наука. Но уже со второй половины XIX в. выдвигается познавательное значение статистики.
ЭКОНОМИЧЕСКАЯ СТАТИСТИКА – это отрасль статистики, изучающая количественную сторону массовых экономических явлений неразрывной связи с их качественной стороной. Она исследует закономерности общественной экономической жизни в конкретном проявлении в определенных условиях времени и места. ОБЪЕКТ ИЗУЧЕНИЯ – процессы расширенного воспроизводства общественного продукта, условия его осуществления и конечные результаты о народном хозяйстве. ПРЕДМЕТ ИЗУЧЕНИЯ– количественная сторона явлений и процессов, происходящих в области экономики, т.е. изучается общественное производство в единстве производительных сил и производственных отношений, влияние природных и технических факторов на количественные изменения в общественной жизни, влияние развития общества и производства на окружающую среду. ОСОБЕННОСТЬ СТАТИСТИЧЕСКОЙ НАУКИ – изучая свой предмет, она изучает свой предмет. Она образует статистические совокупности. СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ – это множество единиц изучаемого явления, объединенных в соответствии с задачей исследования единой качественной основой. Для изучения своего предмета статистика разрабатывает и применяет конкретные методы, совокупность которых образует статистическую методологию. Изучение массовых процессов и явлений в области экономики в экономической статистики основывается на общих принципах статистического метода, который объединяет в себе: 1. статистическое наблюдение. 2. сводку и группировку статистических материалов. 3. анализ обобщающих показателей.
Вопрос 3. Сводка и группировка статистических данных.
На второй стадии статистического исследования, собранная в ходе массового наблюдения информация, подвергается статистической обработке: 1. получение итогов по изучаемой совокупности в целом и отдельным ее частям. 2. систематизация по признакам сходства. Важнейший метод второй стадии исследования – метод статистических группировок, позволяющий выделять в изучаемой совокупности социально-экономические типы, т.е. на второй стадии статистического исследования осуществляется переход от характеристик единичного сводным обобщающим показателем совокупности в целом или ее частей. СВОДКА – это обработка данных, пересчет групповых и общих итогов для получения обобщающих показателей. По сложности сводки бывают: 1. простые 2. сложные Простая сводка представляет общие итоги по изучаемой совокупности в целом, без какой либо предварительной систематизации собранного материала. Она может быть вспомогательной, если представленная в ней информация используется в дальнейшем для более глубокого изучения. Сложная сводка предполагает систематизацию и группировку числовых данных, характеристику образованных групп системой показателей. Подсчет соответствующих итогов и представление результатов сводки в виде таблиц, графиков. Способ разработки статистической сводки может быть: 1. централизованным 2. децентрализованным Централизованный способ. Все данные сосредоточиваются в одном месте и сводятся по одной схеме. Децентрализованный способ. Обобщение материала осуществляется постепенно снизу доверху по иерархической лестнице управления, подвергаясь на каждом этапе соответствующей обработке.
Лекция № 2.
ГРУППИРОВКА – это разделение единиц совокупности по какому-либо существенному признаку. ПРИЗНАК – характерное свойство изучаемого явления, отличающий его от других явлений. Признаки выражены смысловыми понятиями называются атрибутивными. Если атрибутивные признаки принимают только одно из противоположных значений, она называются альтернативными. Признаки, выраженные числовыми значениями, называются количественными. Признаки, принимающие различные значения, отдельных единиц, изучаемого явления называются варьирующими. Значения варьирующего признака отдельных единиц называется вариантой или вариантом. В конкретном исследовании признаки могут подразделяться на основные (существенные), определяющие главное содержание изучаемого явления, и второстепенные (не существенные) не связанные напрямую с основным содержанием. Виды группировок: 1. типологические. Разделение качественно не однородной совокупности на классы, социально-экономические типы, однородные группы. Основная цель у такой группировки идентификация типов. Поэтому, первоочередное значение имеет выбор группировочного признака. 2. структурные. Характеризуют состав однородной совокупности по определенным признакам, объемы явления, значимость отдельных групп. Частный случай структурной группировки – ряд распределения, элементы которого
Ряд распределения
ЧАСТОТЫ – это количество единиц совокупности, которым свойственны конкретные варианты. Вместо частот могут быть относительные величины. Например, проценты к итогу. В статистике относительные частоты принято называть частостями. Оба вида группировок (типологическая и структурная) описательные, характеризуют частей совокупности, выделяя е характерные черты и особенности. Отличаются по уровню качественных различий между группами. 3. аналитическая группировка. С ее помощью проверяют наличие и направление связей между двумя признаками, один из которых является результатом, второй – фактором, влияющим на результат. В классическом варианте аналитической группировки совокупность делится на группы по признаку фактору, затем в каждой группе определяется средний уровень результативного признака. После определения группировочного признака необходимо распределить единицы совокупности по группам. Появляются 2 взаимосвязанных вопроса (число групп и величина интервала). Количество групп во многом зависит от группировочного признака. Например, атрибутивный признак часто предопределяет число групп. По аналогии действуем, если группировочный признак дискретный, изменяющийся в незначительном интервале. ВЕЛИЧИНА ИНТЕРВАЛА – это разность между максимальным и минимальным значениями признаков в каждой группе. Интервалы могут быть равными и неравными. Число групп во многом связано с объемом совокупности. Очень часто устанавливается конкретными целями исследования. Для равных интервалов существует ориентировочная формула. Формула Стерджесса: n – объем совокупности к – число групп к=1+1,322*lg n
Статистические таблицы.
Результаты сводки и группировки материалов наблюдения, как правило, представляются в виде статистических таблиц. Это наиболее рациональная форма представления результатов статистической сводки. Статистическая таблица имеет свое подлежащее и сказуемое. Подлежащее таблицы показывает, о каком явлении идет речь в таблице, и представляет собой группы и подгруппы, которые характеризуются рядом показателей. Сказуемым таблицы называются показатели, с помощью которых изучается объект, т.е. подлежащее таблицы. В основном в сказуемом отражаются численные значения и характеристики изучаемого явления. Обычно составные части изучаемого объекта, образующие подлежащее, располагают в левой части таблицы, а показатели, составляющие сказуемое, помещают справа. Но бывает и обратное расположение подлежащего и сказуемого таблиц, обусловленное целями исследования, характером материала. Составленная и оформленная статистическая таблица должна иметь общий, боковые и верхние заголовки. Общий заголовок обычно располагается над таблицей и выражает ее основное содержание. Таблица иногда может и не иметь общего заголовка, если она вмонтирована в текст. В таком случае дается подробное разъяснение ее содержания в текстовой части. Помещенные, как правило, слева боковые заголовки раскрывают содержание строк подлежащего, а верхние – вертикальных граф (сказуемого таблицы). Простые таблицы получили большое распространение во многих экономических разработках. Они не содержат в подлежащем систематизации изучаемых единиц статистической совокупности. Групповые статистические таблицы дают более информативный материал для анализа изучаемых явлений благодаря образованным в их подлежащем группам по существенному признаку или выявлению связи между рядом показателей. Сказуемое должно быть построено так, чтобы с помощью системы его показателей можно было получить полную характеристику выделенных групп, охватить их существенные черты. В зависимости от задачи исследования и характера исходной информации сказуемое статистических таблиц бывает простым и сложным. Показатели сказуемого при простой разработке располагаются последовательно один за другим. Распределяя показатели на группы по одному или нескольким признакам в определенном сочетании, получают сложное сказуемое.
На третьей заключительной стадии статистического исследования проводится анализ статистической информации, на основе применения обобщающих статистических показателей: 1. абсолютных 2. относительных 3. средних 4. статистические коэффициенты
Лекция №3.
ОПИ – относительные показатели интенсивности. Показываю насколько широко распространено, изучаемое явление, в той или иной среде. Характеризуют отношение разноименных, но связанных между собой показателей.
ОПИ всегда именованные величины. Например, число врачей на 10000 населения. Частный случай ОПИ, относительные показатели экономического развития (ОПЭР) характеризуют некоторые макроэкономические показатели в расчете на душу населения.
ОПС – относительный показатель сравнения. Характеризует количественное соотношение одноименных показателей, относящихся к разным объектам наблюдения.
Вопрос.
СРЕДНЯЯ ВЕЛИЧИНА – обобщающий показатель, который выражает типичные черты и дает обобщающую количественную характеристику какого – либо уровня, какого – либо варьирующего признака по совокупности однородных явлений. Основные формулы для вычисления средних могут быть получены на основе формулы степенной средней.
х – осредняемый признак, тогда хj- варианты, fj – частоты или количество повторов индивидуальных значений признака. Виды средних величин: 1. простая или не взвешенная средняя. Применяется, если отдельные значения, изучаемые не повторяются. 2. взвешенные. Применяются, если отдельные значения в изучаемой совокупности повторяются.
Средняя арифметическая исчисляется в тех случаях, когда общий объем осредняемого признака образуется как сумма его значений об отдельных единиц совокупности. Например, требуется вычислить средний стаж работников. Их стаж xj – 6,5,4,3,3,4,5,4,5,4.
Чаще среднее рассчитывают по сгруппированным данным:
Получаем формулу средней арифметической:
Взвешенная средняя учитывает различные значения отдельных вариант в пределах совокупности. Поэтому применяется, если варианты имеют различную численность. Арифметическая средняя распределяет поровну между объектами общую величину признака. В качестве частот могут быть взяты не только абсолютные, но и относительные величины (частости).
Часто вычисления средней приходится производить по данным сгруппированным в виде интервальных рядов. При этом необходимо в каждом интервале определить серединное значение. А затем произвести взвешивание найденных значений обычным порядком. Иногда первые и последние интервалы могут быть открытыми (нет границ). Тогда при вычислении серединного значения предполагаем, что расстояние между границами данного интервала такое же как в соседнем. Например.
Изложенный выше метод является вынужденным, если нет прямых данных о величине конкретных вариантов. Метод основан на предположении, что отдельные варианты равномерно распределены внутри интервала. В действительности это может быть не так. Тогда середина интервала может отличаться от настоящей средней. Т.е. метод является приближенным. Степень расхождения зависит от следующих причин: 1. число вариант (n). Чем больше вариант, тем меньше ошибка. 2. величина интервала. Чем меньше величина интервалов, тем меньше ошибка. 3. характер распределения. Чем симметричней распределение, тем меньше ошибка. 4. принцип построения интервального ряда. При равных интервалах ошибка меньше. Наличие открытых интервалов может увеличивать ошибку.
Основные свойства средней арифметической: 1. от уменьшения или увеличения частот каждого значения признака, в одно и то же число раз, величина средней арифметической не изменится.
Именно это свойство позволяет при расчетах заменять абсолютные частоты относительными.
2. общий множитель можно выносить за знак средний
3. A* const, 4. все хj =c, c – const =>
5. Изложены свойства позволяют во многих случаях упростить среднее. Из каждого значения х вычитается некоторая постоянная величина. Полученные разности сокращают на общий множитель. Вычисляют среднюю.
Из таблицы (с 3 столбца). А – центральная варианта ряда. Если вариант 2, то ставится та, у которой большая частота. А=550 i – величина интервала i = 100
Лекция №4.
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ – величина, применяющаяся в случаях, когда исходная информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.
Например, по трем городам имеются данные о цене и сумме реализации некоторого товара.
Т.е. средняя гармоническая является превращенной формой средней арифметической.
Например, машина проехала путь в одну сторону со скоростью 80 км/ч, а в другую сторону этот же путь со скоростью 60 км/ч. Определить среднюю скорость.
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ – величина, используемая как средняя из отношений или в рядах распределения представленных в виде геометрической прогрессии. Например, среднегодовые темпы роста.
Структурные средние. Показатели: 1. мода. МОДА – значение признака, наиболее часто встречающееся в исследуемой совокупности. Например 2 – 0 3 – 13 4 – 32 5 – 10 Мода из ряда распределения оценок – 4.
2. медиана МЕДИАНА – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Для дискретных рядов распределения с нечетным числом членов медианой является варианта, стоящая в середине ранжированного ряда. Если ранжированный ряд имеет четное число элементов, то медианой будет среднее арифметическое из двух серединных величин. Медиана практически выполняет функцию средней для неоднородной неподчиняющейся нормальному закону распределения совокупности. Например, представим совокупность, в которой 99 человек имеют доход от 100 до 200 долларов, 1 – 50000
В среднем около 150 $
Рассмотрим на примере нахождение моды и медианы по сгруппированным данным. Имеются данные о тарифном разряде бригадным рабочим.
fmax=60 =>M0 = 5 разряд
Me = 4 разряд
В интервальных рядах распределения мода и медиана вычисляется на основе следующих формул:
Модальным является интервал с наибольшей частотой.
медианным является интервал, в котором впервые Например
Аналогично нахождение медианы можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на 4 части (квартили), на 5 частей (квинтили), на 10 частей (децили), на 100 частей (перцентели).
Лекция № 5. ПОКАЗАТЕЛИ ВАРИАЦИИ (§6) Различия индивидуальных значений признака внутри изучаемой совокупности называется ВАРИАЦИЕЙ ПРИЗНАКА. Она возникает в результате того, что индивидуальные значения складываются под влиянием разных факторов, условий, которые по-разному сочетаются отдельном случае. Средняя не дает представление о том, как отдельные значения признака группируются вокруг средней. Если отдельные значения близко примыкают к средней, то средняя хорошо представляет всю совокупность. Иначе нет. Колеблемость отдельных значений признака характеризуют показатели вариации. В статистике под вариацией понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию случайную и систематическую. Изучая систематическую вариацию можно оценить, насколько однородной является изучаемая совокупность в количественном, а иногда и качественном отношении, и насколько характерной для нее является исчисленная средняя.
§ 6.1. Абсолютные или средние показатели вариаций. Способы их расчета.
1. размах вариации Улавливает только крайние отклонения, не отражает всех вариант в ряду. 2. среднее линейное отклонение В качестве меры вариации признака применяют в статистической практики редко. Данный показатель во многих случаях не устанавливает степень рассеивания. 3. дисперсия (средний квадрат отклонений) 4. среднее квадратическое отклонение (СКО)
Свойства: 1. если к каждому значению вариант добавить (вычесть) одно и то же постоянное число, то дисперсия не изменится. 2. если каждое значение вариант увеличить (уменьшить) в k раз, то дисперсия увеличится или уменьшится в 3. если исчислить средний квадрат отклонений от любой величины, которая отличается от средней арифметической, он будет больше среднего квадрата отклонений от средней арифметической, т.е. больше дисперсии. 4. если все частоты признака увеличить (уменьшить) в одно и то же число раз, то дисперсия не изменится.
Изложенные свойства позволяют вывести формулу для вычисления дисперсии.
5. квартильное отклонение
§ 6.2. Показатели относительного рассеивания.
1. коэффициент осуилляции 2. относительное линейное отклонение (линейный коэффициент вариации)
3. коэффициент вариации Коэффициент вариации является критерием надежности средств. Если он меньше 33%, то можно говорить об однородности совокупности и надежности средней для этой совокупности, иначе наоборот (вытекает из правила 3х сигма в курсе теории вероятности). 4. коэффициент квартельной вариации 5. коэффициент децельной дифференциации
§ 6.3. Дисперсия альтернативного качественного признака
Обозначим наличие изучаемого признака цифрой 1, а отсутствие 0. Пусть доля единиц обладающих признаком составляет p, а не обладающих q. p+q=1.
§ 6.4. Виды дисперсий и правило их сложения
На ряду с изучением вариации признака по всей совокупности может возникнуть необходимость проследить количественные изменение признака, на которые они разбиты, а так же на группы. В этом случае различают дисперсию: 1. общую
2. внутригрупповую 3. межгрупповую
4. средняя из внутригрупповых
Закон сложения дисперсии
Эмпирический коэффициент детерминации
Показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака (часто измеряется в %). Эмпирическое корреляционное отношение
Говорят, что зависимость между результативным или группировочным признаками больше, если Лекция №6. §7 ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ. ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЯ. НОРМЫ РАСПРЕДЕЛЕНИЯ. В некоторых рядах распределения с увеличением значительного варьирующего признака частоты первоначально увеличиваются, а затем после достижения max значения в середине интервала, снижаются. Это свидетельствует о том, что частоты изменяются закономерно в связи с изменением признака. Такие явления называют ЗАКОНОМЕРНОСТЯМИ РАСПРЕДЕЛЕНИЯ. Одна из важнейших целей изучения статистических вариаций рядов - выявить законность распределения и определить ее характер. Как и все статистические законности, законности распределения проявляются в классовом числе наблюдений. При этом необходимо правильно построить вариационный ряд – определить оптимальное число групп и величину интервалов, при которых законности проявляются наиболее отчетливо, если трудно, то совокупность разбивается на max числа групп, затем, укрепление интервала и тем самым уменьшение числа групп, который характер распределения проявляется наиболее четко. Основная задача анализа вариационных рядов – выявить подлинную законность путем исключения влияния второстепенных, случайных для данного распределения фактов, достигается путем увеличения объема исследуемой совокупности при одновременном уменьшении интервала.
Истограмма
f3 →полигон f2
f1
x1 x2 x3 x4 х
Из математической статистики известно, что если увеличить объем совокупности и уменьшить интервалы группировки, то полигон распределения, все более и более приближен к плавной линии – КРИВОЙ РАСПРЕДЕЛЕНИЯ. ТЕОРИТИЧНОСТЬ КРИВОЙ РАСПРЕДЕЛЕНИЯ – называется кривая, сопровождающая общую закономерность данного типа распределения в чистом виде, исключая влияния случайных факторов, т.е. исследуемая эмпирическая модель сводится к идеализированной, теоретичности (а они в свою очередь хорошо изучены). Виды кривой распределения: 1. одновременные кривые - симметричные - условно симметричные - крайне симметричные 2. многовеличинные кривые Как правило, для однородных совокупностей характерны одновременные кривые. Многовероятность свидетельствует о неоднородности данных. При появлении 2х и более вершин необходимо провести перегруппировку с целью выявления однородных групп. Выяснение общего характера распространено предполагает выявление его однородности.
Формулы Линдберга
As=P-50 P – удельный вес в % количество тех вариант, которые превосходят Ек=Р-38,29 Р – доля в %, количество вариант, лежащих в интервале = половине СКО(сигме) в ту или другую строну от средней арифметической в общем количестве вариант.
Определение асимметрии и эксцесса имеет не только описательное значение, они дают определенные указания для дальнейшего исследования социальных явлений. А так же позволяют сделать вывод о возможном применении данного распределения к типу кривых нормальных распределений.
Необходимый объем выборки
Пример 3. В микрорайоне проживает 5000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.142.113 (0.027 с.) |

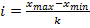 .
.

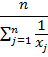
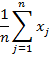



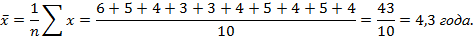
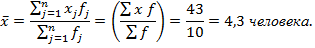





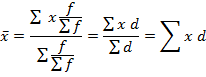



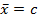

 .формула называется «Способ моментов или способ отсчета от условного нуля».
.формула называется «Способ моментов или способ отсчета от условного нуля».



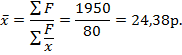


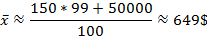




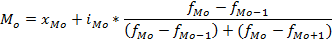


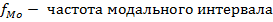

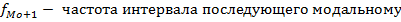
 , n- объем совокупности
, n- объем совокупности








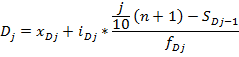
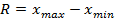

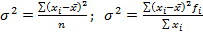

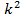 раз. А СКО в k раз.
раз. А СКО в k раз.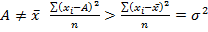


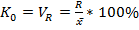
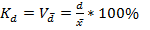





 суммирование идет по всей совокупности. Измеряет вариацию признака во всей совокупности под влиянием всех факторов обусловивших эту вариацию.
суммирование идет по всей совокупности. Измеряет вариацию признака во всей совокупности под влиянием всех факторов обусловивших эту вариацию.
 .
. – общее среднее по всей совокупности
– общее среднее по всей совокупности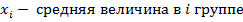


 - общая дисперсия
- общая дисперсия изменяется от 0 до 1 либо от 0 до 100%
изменяется от 0 до 1 либо от 0 до 100% изменяется в пределах от 0 до 1
изменяется в пределах от 0 до 1 больше 0,7.
больше 0,7. в общем числе вариант.
в общем числе вариант.