
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Предмет, метод и задачи статистикиСодержание книги
Поиск на нашем сайте
Вопросы к экзамену по курсу «Статистика» 1. Предмет, метод и задачи статистики. Основные понятия статистики как науки. 2. Понятие статистического наблюдения, его содержание и задачи. Источники статистической информации. Организация статистических работ. 3. Организационные формы, виды и способы статистического наблюдения. 4. Статистические методы классификации и группировки. 5. Задачи и виды группировок. Правила построения группировок. 6. Классификация, виды и типы показателей, используемых при статистических измерениях. 7. Виды абсолютных величин. Единицы измерения абсолютных величин. 8. Виды относительных величин. Формы выражения относительных величин. 9. Сущность и значение средних величин. Виды средних величин. 10. Мода и медиана, порядок расчета и область применения. 11. Абсолютные и относительные показатели вариации. 12. Дисперсия признака. Виды дисперсий. Использование дисперсий в корреляционном анализе. 13. Понятие и основные задачи корреляционного анализа взаимосвязи показателей. Оценка тесноты связи между количественными признаками. 14. Парная корреляция. Понятие и основные задачи регрессионного анализа Построение линейного уравнения регрессии. Коэффициент регрессии. 15. Оценка тесноты связи между качественными признаками. 16. Понятие о выборочном наблюдении. Ошибки выборочного наблюдения. 17. Определение необходимой численности выборки. 18. Виды выборочного наблюдения и их особенности. 19. Статистические методы анализа динамики социально-экономических явлений. 20. Виды рядов динамики и принципы их построения. 21. Показатели ряда динамики и методы их исчисления. 22. Средние показатели интервального и моментного ряда динамики. 23. Методы выявления трендов. Метод скользящей средней, особенности её расчёта. 24. Аналитическое выравнивание рядов динамики. Выравнивание ряда динамики по прямой. 25. Методы прогнозирования рядов динамики. 26. Общее понятие об индексах экономических показателей. Виды индексов. Правила построения индексов. 27. Методы расчета индексов. Агрегатные и средние из индивидуальных индексов. 28. Индексы цен, себестоимости и производительности труда. 29. Использование индексов в экономическом анализе. 30. Основные принципы построения системы национальных счетов. 31. Статистический анализ производительности труда. 32. Статистический анализ основных фондов. 33. Статистический анализ оборотных фондов. 34. Статистический анализ оплаты труда и расходов на персонал 35. Статистический анализ рабочего времени 36. Статистический анализ себестоимости продукции, прибыли и рентабельности. 37. Показатели численности населения. Социально-экономические группировки населения. Изучение состава населения. 38. Статистический анализ воспроизводства и миграции населения. 39. Статистический анализ трудовых ресурсов. Методы исчисления трудовых ресурсов. Показатели воспроизводства и использования трудовых ресурсов. 40. Статистический анализ экономически активного населения. Классификация населения по статусу в занятости. ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ Цель изучения дисциплины – формирование теоретических знаний и практических навыков при сборе, обработке и анализе статистических данных. Задачи дисциплины: изучение теоретических основ о методах, формах, принципах статистического исследования общественных явлений; освоение методов статистического анализа; получение навыков и умений по расчету статистических показателей. Предметом изучения дисциплины являются следующие объекты: количественная сторона массовых общественных явлений и процессов и закономерностей их развития в конкретных условиях места и времени общие принципы и методы статистического исследования общественных явлений, наиболее общие показатели статистики. статистическая информация, отражающая тенденции развития, взаимосвязи и взаимообусловленности протекающих социально-экономических процессов. ТЕМА 1. ПРЕДМЕТ, МЕТОД И ЗАДАЧИ СТАТИСТИКИ Статистика – это наука, которая изучает количественную сторону массовых социально-экономических явлений в неразрывной связи с их качественной стороной, а также количественное выражение закономерностей развития процессов в конкретных условиях места и времени. Предмет статистики — количественная сторона массовых социально-экономических явлений и процессов. Методы статистики — метод массовых наблюдений, метод группировок, методы анализа с помощью обобщающих показателей. Статистическая совокупность — это множество подвергающихся статистическому исследованию объектов или явлений, объединенных общими признаками, из которых один или несколько признаков не варьируют. Единица совокупности — индивидуальный составной элемент статистической совокупности, являющийся носителем изучаемых признаков. Признак — это объективная характеристика единицы статистической совокупности, характерная черта или свойство, которое может быть определено или измерено. Вариант — возможное значение, которое может принимать признак. Вариация — изменчивость, многообразие значений (вариантов) признака. Объем совокупности — общее число единиц, образующих статистическую совокупность. Объем признака — суммарное значение признака по всем единицам совокупности. Признаки по форме выражения бывают количественные (дискретные и непрерывные) и качественные (атрибутивные, порядковые, альтернативные). Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. В отличие от признака статистический показатель получается расчетным путем. Статистические показатели по форме выражения разделяются на абсолютные, относительные и средние. По временному фактору показатели бывают моментные (по состоянию на дату) и интервальные (за период). Основные отрасли статистики — теория статистики, математическая статистика, экономическая статистика (микро- и макро-), социальная статистика, отраслевые статистики (промышленности, сельского хозяйства, капитального строительства, транспорта и связи, торговли…). Центральным органом государственной статистики является Федеральная служба государственной статистики РФ (Росстат). В регионах имеются территориальные органы Росстата. ТЕМА 2. СТАТИСТИЧЕСКОЕ ИЗМЕРЕНИЕ И НАБЛЮДЕНИЕ Статистическое наблюдение – первый этап статистического исследования. Результат его является массив исходных данных об изучаемом объекте (первичная информация). Эта информация не публикуется. Статистическое наблюдение — это научно организованный, планомерный и систематический процесс сбора массовых сведений о социально-экономических явлениях и процессах путем регистрации заранее намеченных существенных признаков. Требования, предъявляемые к статистической информации — достоверность и сопоставимость данных. Программно-методологические вопросы наблюдения — цели и задачи, объект, единицы наблюдения, единица совокупности, программа наблюдения, статистический формуляр и инструкции. Организационные вопросы наблюдения — органы наблюдения, место и время проведения наблюдения, критический момент времени наблюдения, подготовка наблюдения и меры по обеспечению достоверности данных. Организационные формы статистического наблюдения — отчетность (основная форма) и специально организованное наблюдение. Виды наблюдения по охвату единиц совокупности — сплошное, несплошное (выборочное, основного массива, монографическое). Виды наблюдения по временному фактору — текущее (непрерывное), периодическое и единовременное. Виды наблюдения в зависимости о источника сведений — непосредственное, документальное, опрос. Способы наблюдения — отчётный, экспедиционный, саморегистрации, анкетный, корреспондентский, явочный. ТЕМА 5. СРЕДНИЕ ВЕЛИЧИНЫ Средняя величина – это обобщающий показатель, который дает количественную характеристику признака в статистической совокупности в условиях конкретного места и времени. Она отражает уровень этого признака, отнесенный к единице совокупности Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. В неоднородной совокупности общие средние должны быть заменены или дополнены групповыми средними, рассчитанными по однородным группам. Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение (ИСС) для расчета средней. Выбор вида средних зависит от исходных данных и содержания определяемого показателя.
Например, расчет средней зарплаты ведется по логической формуле:
Может быть известен числитель или знаменатель формулы. От этого и зависит выбор вида средней. Виды средних величин: 1) Степенные (арифметическая, гармоническая, геометрическая, квадратическая и др.) 2) Структурные (мода, медиана, кварти́ли, деци́ли и др.). Элементы степенной средней: Варианта (х) — значения варьирующего количественного признака Число единиц (n) — количество вариант в совокупности. Веса (частоты f или частости ω) — показатели повторяемости вариант в совокупности. Средняя арифметическая простая (невзвешенная) — эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным
Средняя арифметическая взвешенная — эта форма средней используется в тех случаях, когда расчет осуществляется по сгруппированным данным и неизвестен числитель в логической формуле:
Веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). При расчете средней по интервальному вариационному ряду используют середину интервала. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). Пример 5.1. Объем производства и себестоимость продукции, производимой тремя предприятиями, характеризуются следующими данными:
Определить среднюю себестоимость одного изделия. Решение: составим логическую формула для расчета
Неизвестен числитель в логической формуле.
Пример 5.2. Имеются данные о распределении выданных банком кредитов по их размеру
Определить средний размер кредита. Решение: составим логическую формула для расчета
Составим рабочую таблицу:
Середины интервалов находится следующим образом: для закрытого интервала — средняя арифметическая простая, например x 4=(500+800)/2 = 650 для открытого интервала
Кср = 35300 / 60 = 588,3 тыс.руб. Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель:
где wi = xi ´ fi Пример 5.3. Имеются данные о результаты биржевых торгов по акциям эмитента.
Определить средний курс акции. Решение: составим логическую формула для расчета
Числитель мы получим простым суммированием объемов сделок по биржам. Надо найти знаменатель.
Средняя гармоническая невзвешенная (простая)
Пример 5.4. Упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 20 мин, второй — 30 мин. Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна? Решение: Для определения средних затрат времени необходимо общие затраты времени разделить на общее число обработанных за этот интервал двумя работниками заказов. Время можно взять любое (480 мин, 60 мин.)
Средняя геометрическая невзвешенная:
где k — количество осредняемых величин; Средняя геометрическая взвешенная:
где fi — вес i -гo варианта. Структурные средние Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Моду можно определить для любого количественного и качественного признака. Мода отражает типичный, наиболее распространенный вариант значения признака. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности. Медиану можно определить только для порядкового качественного признака. Медиана выполняет функции средней для неоднородной совокупности. Пример 5.5. Определить моду и медиану по несгруппированным данным. Даны значения признака группы работников (стаж работы, лет): 5, 2, 4, 3, 4, 2, 2. Решение: чаще всего встречается стаж 2 года, следовательно Мо=2 года. Для определения медианы необходимо провести ранжирование (упорядочивание): 2, 2, 2, 3, 4, 4, 5. В середине ряда — цифра 3, это и есть медиана. Если количество значений четное: 2, 2, 2, 3, 4, 4, 5, 9 Медиана определяется как средняя из двух центральных значений (3 и 4) Ме = (3+4)/2 = 3,5 года. ТЕМА 6. ПОКАЗАТЕЛИ ВАРИАЦИИ Вариация – это колеблемость, многообразие, изменяемость величины (вариантов) признака у отдельных единиц совокупности Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа показателей вычисляется как отношение абсолютных показателей вариации к средней арифметической (или медиане). Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др. Размах вариации (R) — это разность между наибольшим (xmax) и наименьшим (xmin) значениями варьирующего признака: Среднее линейное отклонение (
Дисперсия (s2) представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
Второй способ расчёта дисперсии:
где Среднее квадратическое отклонение (стандартное отклонение) (s):
Среднее квадратическое отклонение показывает, на какую величину в среднем значение признака отличается от среднего значения. Исчисление среднего квадратического отклонения для явно несимметричных распределений не имеет смысла. Виды дисперсий Общая дисперсия s2 измеряет вариацию результативного признака (y) во всей совокупности под влиянием всех факторов (x 1, x 2, x 3…) обусловивших эту вариацию. Межгрупповая дисперсия
где ` yi и ni — соответственно групповые средние и численности по отдельным группам. Внутригрупповая дисперсия (
Средняя из внутригрупповых дисперсий (
Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсией:
В статистическом анализе широко используется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии. Он носит название эмпирического коэффициента детерминации (
Этот коэффициент показывает долю (удельный вес) общей вариации изучаемого признака обусловленную вариацией группировочного признака. Корень квадратный из эмпирического коэффициента детерминации носит название эмпирического корреляционного отношения (h):
Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1. Если h = 0, то группировочный признак не оказывает влияние на результативный. Если h = 1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям. Пример 6.4. Имеются данные о группе рабочих.
Оценить силу связи между признаками. Решение: Даны групповые средние и внутригрупповые дисперсии. Определим среднюю общую используя групповые средние
Средняя из внутригрупповых дисперсий
Межгрупповая дисперсия
Общая дисперсия s 2 =6,955 + 34,65 = 41,605 Эмпирический коэффициент детерминации
Эмпирическое корреляционное отношение
Такое значение (близко к 1) характеризует очень сильную связь между числом обслуживаемых станков и средней зарплатой. Основы прогнозирования Исследование динамики социально-экономических явлений, выявление и характеристика основной тенденции развития и моделей взаимосвязи дают основание для прогнозирования — определения будущих размеров уровня экономического явления. Выделяют следующие элементарные методы прогнозирования: по среднему абсолютному приросту, по среднему темпу роста и на основе выравнивания рядов по какой-либо аналитической формуле. Прогнозирование по среднему абсолютному приросту (
где n — номер последнего уровня исследуемого периода, за который рассчитан`D; i — срок прогноза (период упреждения). Прогнозирование по среднему темпу роста осуществляется в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста (
где уn — последний уровень ряда динамики; i — срок прогноза; Наиболее распространенным методом прогнозирования считают аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t). При таком подходе к прогнозированию предполагается, что размер уровня, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, т. е. у = f(t). При выборе типа линии можно учитывать следующее: - прямая линия — если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины; - парабола второго порядка (полином) — если приросты приростов уровней (ускорения) колеблются около постоянной величины; - показательная функция (экспонента) — если уровни изменяются с приблизительно постоянным относительным приростом. Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, имеет малую вероятность. Любой статистический прогноз носит приближенный характер. Поэтому целесообразно определение доверительных интервалов прогноза. Точечный прогноз на k шагов вперед получается путем подстановки в модель параметра t=n +1, …, n + k. Доверительный интервал прогноза будет иметь следующие границы: верхняя граница прогноза = yp(n+k) + U(k), нижняя граница прогноза = yp(n+k) – U(k). Величина U(k) для линейной модели имеет следующий вид:
где sy — средняя квадратическая ошибка тренда; yp — расчетное значение уровня (по уравнению); m — число параметров уравнения (для линейного m = 2); n — количество исходных уровней; ` t — среднее значение параметра t (для имеющихся данных); k p — доверительная величина, определяемая на основе t -критерия Стьюдента. Ранговые коэффициенты связи В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Ранжирование — это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения. Ранг — это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической из соответствующих номеров мест, которые они определяют. Данные ранги называются связными. Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена и Кендалла. Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками (рейтинги, уровни образования, квалификации и т.п.). Коэффициент корреляции рангов Спирмена (r):
где n – число наблюдений (число пар рангов); d2i – квадраты разности рангов x и y. Коэффициент Спирмена принимает значения в интервале [-1; 1]. Ранговый коэффициент корреляции Кендалла также может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты и ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле:
где n – число наблюдений; S = P+Q — сумма разностей между числом последовательностей и числом инверсий по второму признаку. Расчет данного коэффициента выполняется в следующей последовательности: Значения x ранжируются в порядке возрастания или убывания; Значения y располагаются в порядке, соответствующем значениям x; Для каждого ранга y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяется величина P, как мера соответствия последовательностей рангов по x и y и учитывается со знаком (+); Для каждого ранга y определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком (-); Определяется сумма баллов по всем членам ряда. Как правило, коэффициент Кендалла меньше коэффициента Спирмена.
Связь между признаками признается статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0,5. Содержание ТЕМА 1. ПРЕДМЕТ, МЕТОД И ЗАДАЧИ СТАТИСТИКИ.. 2 ТЕМА 2. СТАТИСТИЧЕСКОЕ ИЗМЕРЕНИЕ И НАБЛЮДЕНИЕ.. 3 ТЕМА 3. СВОДКА И ГРУППИРОВКА МАТЕРИАЛОВ СТАТИСТИЧЕСКОГО НАБЛЮДЕНИЯ.. 4 ТЕМА 4. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ... 5 ТЕМА 5. СРЕДНИЕ ВЕЛИЧИНЫ... 6 ТЕМА 6. ПОКАЗАТЕЛИ ВАРИАЦИИ.. 13 ТЕМА 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ.. 18 ТЕМА 8. ЭКОНОМИЧЕСКИЕ ИНДЕКСЫ... 28 ТЕМА 9. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ.. 37 ТЕМА 10. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ.. 40
Вопросы к экзамену по курсу «Статистика» 1. Предмет, метод и задачи статистики. Основные понятия статистики как науки. 2. Понятие статистического наблюдения, его содержание и задачи. Источники статистической информации. Организация статистических работ. 3. Организационные формы, виды и способы статистического наблюдения. 4. Статистические методы классификации и группировки. 5. Задачи и виды группировок. Правила построения группировок. 6. Классификация, виды и типы показателей, используемых при статистических измерениях. 7. Виды абсолютных величин. Единицы измерения абсолютных величин. 8. Виды относительных величин. Формы выражения относительных величин. 9. Сущность и значение средних величин. Виды средних величин. 10. Мода и медиана, порядок расчета и область применения. 11. Абсолютные и относительные показатели вариации. 12. Дисперсия признака. Виды дисперсий. Использование дисперсий в корреляционном анализе. 13. Понятие и основные задачи корреляционного анализа взаимосвязи показателей. Оценка тесноты связи между количественными признаками. 14. Парная корреляция. Понятие и основные задачи регрессионного анализа Построение линейного уравнения регрессии. Коэффициент регрессии. 15. Оценка тесноты связи между качественными признаками. 16. Понятие о выборочном наблюдении. Ошибки выборочного наблюдения. 17. Определение необходимой численности выборки. 18. Виды выборочного наблюдения и их особенности. 19. Статистические методы анализа динамики социально-экономических явлений. 20. Виды рядов динамики и принципы их построения. 21. Показатели ряда динамики и методы их исчисления. 22. Средние показатели интервального и моментного ряда динамики. 23. Методы выявления трендов. Метод скользящей средней, особенности её расчёта. 24. Аналитическое выравнивание рядов динамики. Выравнивание ряда динамики по прямой. 25. Методы прогнозирования рядов динамики. 26. Общее понятие об индексах экономических показателей. Виды индексов. Правила построения индексов. 27. Методы расчета индексов. Агрегатные и средние из индивидуальных индексов. 28. Индексы цен, себестоимости и производительности труда. 29. Использование индексов в экономическом анализе. 30. Основные принципы построения системы национальных счетов. 31. Статистический анализ производительности труда. 32. Статистический анализ основных фондов. 33. Статистический анализ оборотных фондов. 34. Статистический анализ оплаты труда и расходов на персонал 35. Статистический анализ рабочего времени 36. Статистический анализ себестоимости продукции, прибыли и рентабельности. 37. Показатели численности населения. Социально-экономические группировки населения. Изучение состава населения. 38. Статистический анализ воспроизводства и миграции населения. 39. Статистический анализ трудовых ресурсов. Методы исчисления трудовых ресурсов. Показатели воспроизводства и использования трудовых ресурсов. 40. Статистический анализ экономически активного населения. Классификация населения по статусу в занятости. ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ Цель изучения дисциплины – формирование теоретических знаний и практических навыков при сборе, обработке и анализе статистических данных. Задачи дисциплины: изучение теоретических основ о методах, формах, принципах статистического исследования общественных явлений; освоение методов статистического анализа; получение навыков и умений по расчету статистических показателей. Предметом изучения дисциплины являются следующие объекты: количественная сторона массовых общественных явлений и процессов и закономерностей их развития в конкретных условиях места и времени общие принципы и методы статистического исследования общественных явлений, наиболее общие показатели статистики. статистическая информация, отражающая тенденции развития, взаимосвязи и взаимообусловленности протекающих социально-экономических процессов. ТЕМА 1. ПРЕДМЕТ, МЕТОД И ЗАДАЧИ СТАТИСТИКИ Статистика – это наука, которая изучает количественную сторону массовых социально-экономических явлений в неразрывной связи с их качественной стороной, а также количественное выражение закономерностей развития процессов в конкретных условиях места и времени. Предмет статистики — количественная сторона массовых социально-экономических явлений и процессов. Методы статистики — метод массовых наблюдений, метод группировок, методы анализа с помощью обобщающих показателей. Статистическая совокупность — это множество подвергающихся статистическому исследованию объектов или явлений, объединенных общими признаками, из которых один или несколько признаков не варьируют. Единица совокупности — индивидуальный составной элемент статистической совокупности, являющийся носителем изучаемых признаков. Признак — это объективная характеристика единицы статистической совокупности, характерная черта или свойство, которое может быть определено или измерено. Вариант — возможное значение, которое может принимать признак. Вариация — изменчивость, многообразие значений (вариантов) признака. Объем совокупности — общее число единиц, образующих статистическую совокупность. Объем признака — суммарное значение признака по всем единицам совокупности. Признаки по форме выражения бывают количественные (дискретные и непрерывные) и качественные (атрибутивные, порядковые, альтернативные). Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. В отличие от признака статистический показатель получается расчетным путем. Статистические показатели по форме выражения разделяются на абсолютные, относительные и средние. По временному фактору показатели бывают моментные (по состоянию на дату) и интервальные (за период). Основные отрасли статистики — теория статистики, математическая статистика, экономическая статистика (микро- и макро-), социальная статистика, отраслевые статистики (промышленности, сельского хозяйства, капитального строительства, транспорта и связи, торговли…). Центральным органом государственной статистики является Федеральная служба государственной статистики РФ (Росстат). В регионах имеются территориальные органы Росстата.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.014 с.) |



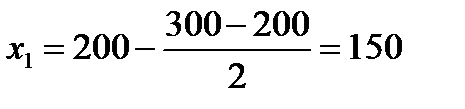

 ,
,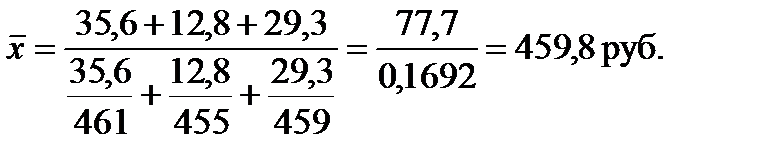
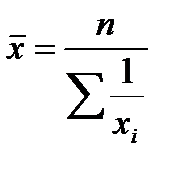

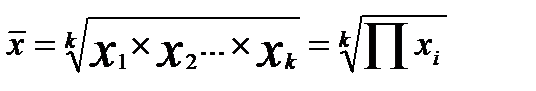

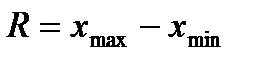
 ) — вычисляется как средняя арифметическая из абсолютных значений отклонений вариант xi от` x:
) — вычисляется как средняя арифметическая из абсолютных значений отклонений вариант xi от` x: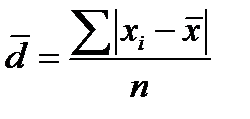 (простое);
(простое);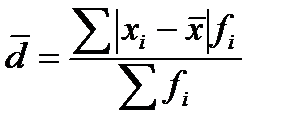 (взвешенное)
(взвешенное)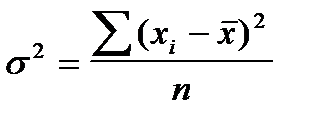 (простая);
(простая);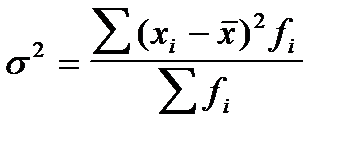 (взвешенная)
(взвешенная)
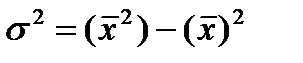
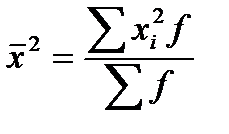 — средняя из квадратов индивидуальных значений
— средняя из квадратов индивидуальных значений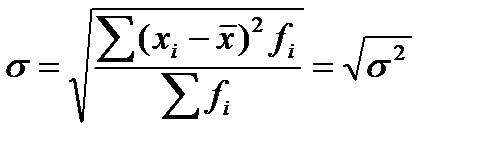
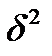 характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора (x), положенного в основание группировки. Она рассчитывается по формуле
характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора (x), положенного в основание группировки. Она рассчитывается по формуле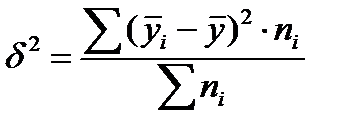 ,
,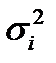 ) отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:
) отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом: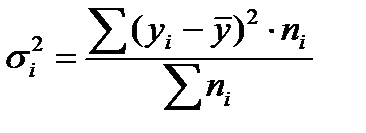
 ):
):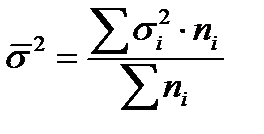
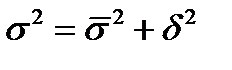
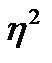 ):
):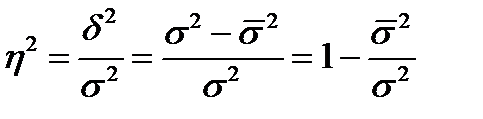 .
. .
.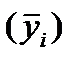
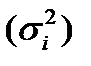
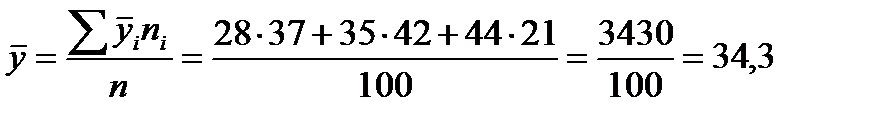 тыс.руб.
тыс.руб.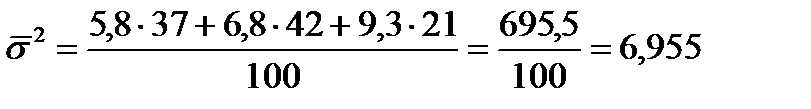
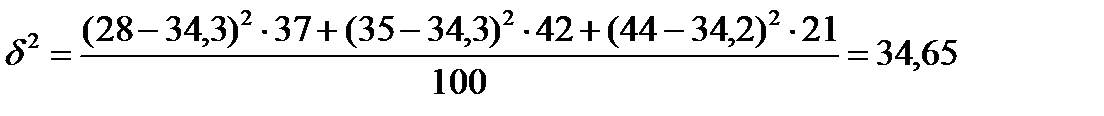
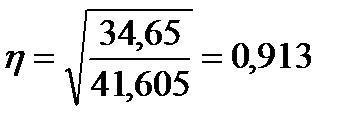
 ) — основано на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов). Экстраполяцию можно сделать по следующей формуле:
) — основано на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов). Экстраполяцию можно сделать по следующей формуле: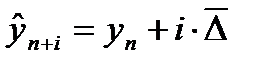
 — экстраполируемый уровень; (n+i) — номер этого уровня;
— экстраполируемый уровень; (n+i) — номер этого уровня; ), возведенный в степень, соответствующую периоду экстраполяции, т. е. по формуле:
), возведенный в степень, соответствующую периоду экстраполяции, т. е. по формуле:


 ,
,



