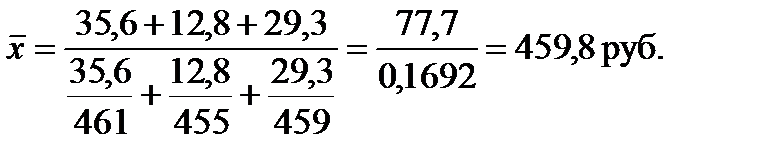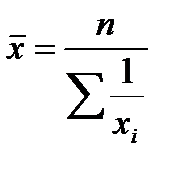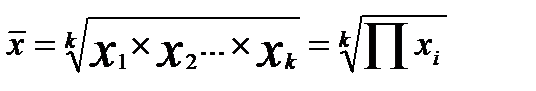Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Абсолютные и относительные величиныСодержание книги
Поиск на нашем сайте
Абсолютная величина – это показатель, выражающие размеры (объемы, уровни) социально-экономических явлений в единицах меры, веса, объема, протяженности, площади, стоимости и т.д. Абсолютные статистические величины — это числа именованные. Они всегда имеют определенную размерность, определенные единицы измерения. Единицы измерения абсолютных величин — натуральные (условно-натуральные), стоимостные или трудовые (чел.-час, чел.-день). Условно-натуральные единицы применяются для сведения воедино нескольких разновидностей одной и той же продукции. Одну из них принимают за эталон, а другие пересчитывают с помощью специальных коэффициентов в единицы меры этого эталона (усл.шт, усл.т, усл.банки…) Относительными величинами называются статистические показатели, выражающие количественные соотношения между явлениями общественной жизни. Они получаются в результате деления одной абсолютной величины на другую. Величина, с которой производится сравнение (знаменатель дроби), обычно называется основанием, базой сравнения, или базисной величиной, числитель — сравниваемая величина, ее называют также текущей, или отчетной величиной Формы выражения относительных величин: - в коэффициентах (база равна 1) - в процентах % (база равна 100) - в промилле ‰ (база равна 1000) - в единицах измерения (чел/км2, руб./чел…) Виды относительных величин: 1) относительная величина планового задания ОВПЗ = Уплан1 / Уфакт0 2) относительная величина выполнения плана ОВВП = Уфакт1 / Уплан1 3) относительная величина динамики ОВД = У i / У0 =ОВПЗ · ОВВП 4) относительная величина структуры ОВС = fi / ∑ fi 5) относительная величина координации ОВК = fi / fj 6) относительная величина сравнения ОВСр = УА / УВ 7) относительная величина интенсивности ОВИ = УА / Среда распространения УА Пример 4.1. Численность населения страны на начало 2012 г. составила 142,7 млн. чел., в т.ч. экономически активное население – 75,2 млн. чел. Население в возрасте моложе трудоспособного из общей численности – 22,8 млн. чел., трудоспособном – 88,2 млн. чел. Численность мужчин – 65,2 млн. чел., женщин – 77,5 млн. чел. Определить показатели структуры и координации. Решение: Структура населения по возрасту 22,8/142,7 = 16,0% – моложе трудоспособного возраста 88,2/142,7 = 61,8% – трудоспособного возраста (142,7-22,8-88,2)/142,7= 22,2% – старше трудоспособного возраста. Структура населения по экономической активности: 75,2/142,7 = 52,7% — экономически активное население (занятые и безработные) (142,7-75,2)/124,7 = 47,3% — экономически неактивное население Показатели координации: 22,8/88,2 = 0,259 или 259 чел. моложе трудоспособного возраста на 1000 чел. трудоспособного возраста. 77,5/65,2 = 1,188 или 1188 женщин на 1000 мужчин ТЕМА 5. СРЕДНИЕ ВЕЛИЧИНЫ Средняя величина – это обобщающий показатель, который дает количественную характеристику признака в статистической совокупности в условиях конкретного места и времени. Она отражает уровень этого признака, отнесенный к единице совокупности Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. В неоднородной совокупности общие средние должны быть заменены или дополнены групповыми средними, рассчитанными по однородным группам. Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение (ИСС) для расчета средней. Выбор вида средних зависит от исходных данных и содержания определяемого показателя.
Например, расчет средней зарплаты ведется по логической формуле:
Может быть известен числитель или знаменатель формулы. От этого и зависит выбор вида средней. Виды средних величин: 1) Степенные (арифметическая, гармоническая, геометрическая, квадратическая и др.) 2) Структурные (мода, медиана, кварти́ли, деци́ли и др.). Элементы степенной средней: Варианта (х) — значения варьирующего количественного признака Число единиц (n) — количество вариант в совокупности. Веса (частоты f или частости ω) — показатели повторяемости вариант в совокупности. Средняя арифметическая простая (невзвешенная) — эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным
Средняя арифметическая взвешенная — эта форма средней используется в тех случаях, когда расчет осуществляется по сгруппированным данным и неизвестен числитель в логической формуле:
Веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). При расчете средней по интервальному вариационному ряду используют середину интервала. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). Пример 5.1. Объем производства и себестоимость продукции, производимой тремя предприятиями, характеризуются следующими данными:
Определить среднюю себестоимость одного изделия. Решение: составим логическую формула для расчета
Неизвестен числитель в логической формуле.
Пример 5.2. Имеются данные о распределении выданных банком кредитов по их размеру
Определить средний размер кредита. Решение: составим логическую формула для расчета
Составим рабочую таблицу:
Середины интервалов находится следующим образом: для закрытого интервала — средняя арифметическая простая, например x 4=(500+800)/2 = 650 для открытого интервала
Кср = 35300 / 60 = 588,3 тыс.руб. Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель:
где wi = xi ´ fi Пример 5.3. Имеются данные о результаты биржевых торгов по акциям эмитента.
Определить средний курс акции. Решение: составим логическую формула для расчета
Числитель мы получим простым суммированием объемов сделок по биржам. Надо найти знаменатель.
Средняя гармоническая невзвешенная (простая)
Пример 5.4. Упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 20 мин, второй — 30 мин. Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна? Решение: Для определения средних затрат времени необходимо общие затраты времени разделить на общее число обработанных за этот интервал двумя работниками заказов. Время можно взять любое (480 мин, 60 мин.)
Средняя геометрическая невзвешенная:
где k — количество осредняемых величин; Средняя геометрическая взвешенная:
где fi — вес i -гo варианта.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.113 (0.008 с.) |



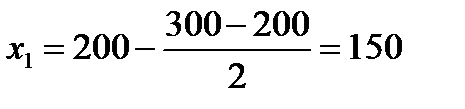

 ,
,