
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 9. Выборочное наблюдениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому наблюдению подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу — по обследуемой части дать характеристику всей (генеральной) совокупности единиц. Совокупность отобранных для обследования единиц называют выборочной, а совокупность единиц, из которых производится отбор, — генеральной. Отбор единиц в выборочную совокупность может быть повторным или бесповторным. При повторном отборе попавшая в выборку единица подвергается обследованию, т. е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения. При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке. Выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности). Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности. Систематические ошибки репрезентативности обусловлены нарушением принципа случайности отбора (тенденциозный отбор) и являются однонаправленными ошибками. Их можно устранить правильной процедурой отбора единиц в выборку. Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей. Выборка характеризуется следующими показателями: средняя ошибка выборки (повторный отбор):
средняя ошибка выборки (бесповторный отбор):
предельная ошибка выборки — ошибка, исчисленная с заданной степенью вероятности:
где s2 — выборочная дисперсия (значения признака или доли), n — объем выборочной совокупности; N — объем (число единиц) генеральной совокупности;
ω — выборочная доля (
t — коэффициент доверия (табличное значение). Предельная ошибка выборки дает возможность выяснить, в каких пределах находится величина генеральной средней с учетом заданной вероятности; На величину вероятности указывает множитель t. Обычно используются нормированные (табличные) значения t, для определенных значений вероятности Ф(t):
Зная выборочную среднюю величину признака (
Зная выборочную долю признака (
Для типической выборки при расчете средней ошибки (m) используют не общую дисперсию, а среднюю из внутригрупповых дисперсий ( Для определения необходимой численности выборки исследователь должен задать уровень точности (предельную ошибку) выборочной совокупности с определенной вероятностью. Численность случайной повторной выборки определяется по формуле:
бесповторной:
где Если расчет проводится по качественному альтернативному признаку и не известна его доля в генеральной совокупности, её принимают равной 0,5, так как дисперсия доли достигает максимума:
Пример 9.1. Для определения качества партии товара 5% от всего количества изделий были подвергнуты выборочному обследованию. Из 1000 проверенных изделий 150 были нестандартными. Определить с вероятностью 0,954 долю нестандартных изделий во всей партии. Решение: По условию задачи дано:
Определим предельную ошибку выборочного наблюдения:
Δ ω = t
или Δω = 2 Доверительные интервалы для доли будут равны: p = w p = 15% Доля нестандартных изделий во всей партии будет находиться в пределах от 12,8 до 17,2% при вероятности 0,954. Пример 9.2. Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 10%-ная механическая выборка, в которую попало 200 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. С вероятностью 0,997 определить пределы, в которых будет находиться средний срок пользования краткосрочным кредитом в генеральной совокупности. Решение. Средний срок пользования кредитом в банке находится в пределах:
Так как выборка механическая, то ошибка выборочного наблюдения определяется по формуле: Δх = t
Δх = 3
С вероятностью 0,997 можно утверждать, что средний срок пользования краткосрочным кредитом в банке находится в пределах от 28 дней до 32 дней.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.009 с.) |

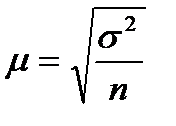


 – выборочная дисперсия значения признака (х);
– выборочная дисперсия значения признака (х);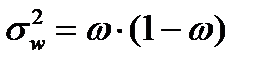 – выборочная дисперсия доли;
– выборочная дисперсия доли; ), т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности;
), т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности; — выборочная средняя;
— выборочная средняя; ) и предельную ошибку выборки (Dx), можно определить границы (пределы), в которых заключена генеральная средняя (
) и предельную ошибку выборки (Dx), можно определить границы (пределы), в которых заключена генеральная средняя ( ):
): или
или 
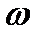 ) и предельную ошибку выборки (
) и предельную ошибку выборки (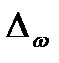 ), можно определить границы, в которых заключена генеральная доля (р):
), можно определить границы, в которых заключена генеральная доля (р):
 ), при серийной выборке — межгрупповую дисперсию (d 2).
), при серийной выборке — межгрупповую дисперсию (d 2). , или
, или 
 .
. или
или  — относительная ошибка выборки
— относительная ошибка выборки — коэффициент вариации
— коэффициент вариации = 0,25 при ω = 0,5.
= 0,25 при ω = 0,5.
 = 5% или 0,05
= 5% или 0,05
 =
=  = 0,15 или 15%.
= 0,15 или 15%.

 = 0,022 или 2,2%.
= 0,022 или 2,2%. Δw
Δw p
p  – Δх
– Δх 
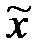 + Δх .
+ Δх . ;
; = 1,81
= 1,81  2 дня
2 дня =30 дн.
=30 дн. 


