
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие выборочного наблюденияСодержание книги
Поиск на нашем сайте Выборочный метод используется, когда применение сплошного наблюдения физически невозможно из-за огромного массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением. Например, дегустация, испытание кирпичей на прочность и т.п. Выборочное наблюдение используется также для проверки результатов сплошного. Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весьих массив - генеральную совокупность (ГС). При этом число единиц в выборке обозначают п, во всей ГС – N. Отношение n/N называется относительный размер или доля выборки. Качество результатов выборочного наблюдения зависит от репрезентативности выборки, т.е. от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.. Способы формирования выборки 1. Собственно случайный отбор: все единицы ГС нумеруются, а выпавшие в результате жеребьевки номера соответствуют единицам, попавшим в выборку, причем число номеров равно запланированному объему выборки. На практике вместо жеребьевки используют генераторы случайных чисел. Данный способ отбора может быть повторным (когда каждая единица, отобранная в выборку, после проведения наблюдения возвращается в ГС и может быть вновь подвергнута обследованию) и бесповторным (когда обследованные единицы в ГС не возвращаются и не могут быть обследованы повторно). При повторном отборе вероятность попадания в выборку для каждой единицы ГС остается неизменной, а при бесповторном отборе она меняется (увеличивается), но для оставшихся в ГС после отбора из нее нескольких единиц, вероятность попадания в выборку одинакова. 2. Механический отбор: отбираются единицы генеральной совокупности с постоянным шагом N/п. Так, если она генеральная совокупность содержит 100 тыс.ед., а требуется выбрать 1 тыс.ед., то в выборку попадет каждая сотая единица. 3. Стратифицированный (расслоенным) отбор осуществляется из неоднородной генеральной совокупности, когда ее предварительно разбивают на однородные группы, после чего производят отбор единиц из каждой группы в выборочную совокупность случайный или механическим способом пропорционально их численности в генеральной совокупности. 4. Серийный (гнездовой)отбор: случайным или механическим способом выбирают не отдельные единицы, а определенные серии (гнезда), внутри которых производится сплошное наблюдение. Средняя ошибка выборки После завершения отбора необходимого числа единиц в выборку и регистрации предусмотренных программой наблюдения изучаемых признаков этих единиц, переходят к расчету обобщающих показателей. К ним относят среднюю величину изучаемого признака и долю единиц, обладающих каким-либо значением этого признака. Однако, если ГС произвести несколько выборок, определив при этом их обобщающие характеристики, то можно установить, что их значения будут различными, кроме того, они будут отличаться и от реального их значения в ГС, если такое определить с помощью сплошного наблюдения. Другими словами, обобщающие характеристики, рассчитанные по данным выборки, будут отличаться от их реальных значений в ГС, поэтому введем следующие условные обозначения (табл. 23). Таблица 23. Условные обозначения
Разность между значением обобщающих характеристик выборочной и генеральной совокупностей называется ошибкой выборки, которая подразделяется на ошибку регистрации и ошибку репрезентативности. Первая возникает из-за неправильных или неточных сведений по причинам непонимания существа вопроса, невнимательности регистратора при заполнении анкет, формуляров и т.п. Она достаточно легко обнаруживается и устраняется. Вторая возникает из-за несоблюдения принципа случайности отбора единиц в выборку. Ее сложнее обнаружить и устранить, она гораздо больше первой и потому ее измерение является основной задачей выборочного наблюдения. Для измерения ошибки выборки определяется ее средняя ошибка по формуле (65) для повторного отбора и по формуле (66) – для бесповторного:
Из формул (65) и (66) видно, что средняя ошибка меньше у бесповторной выборки, что и обусловливает ее более широкое применение. Предельная ошибка выборки Учитывая, что на основе выборочного обследования нельзя точно оценить обобщающую характеристику ГС, необходимо найти пределы, в которых он находится. В конкретной выборке разность
где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки. Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме Чебышёва, при достаточно большом объеме выборки и ограниченной дисперсии генеральной ГС вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:
А. М. Ляпунов доказал, что независимо от характера распределения генеральной ГС при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению (центральная предельная теорема). Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:
где Значения P (интеграла Лапласа) для разных t рассчитаны и имеются в специальной таблице, которая приведена в Приложении 1. Вероятность, которая принимается при расчете выборочной характеристики, называется доверительной. Чаще всего принимают вероятность P = 0,950, которая означает, что только в 5 случаях из 100 ошибка может выйти за установленные границы. Задавшись конкретным уровнем вероятности, выбирают величину нормированного отклонения t по Приложению 1 и рассчитывают предельную ошибку выборки по формуле (67). После расчета предельной ошибки находят доверительный интервал обобщающей характеристики ГС совокупности по формуле (70) – для среднего значения, и по формуле (71) – для доли единиц, обладающих каким-либо значением признака:
Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики ГС, а лишь ее доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |



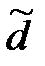



 =
=  ;(65)
;(65)  . (66)
. (66) может быть больше, меньше или равна
может быть больше, меньше или равна  . Каждое из отклонений
. Каждое из отклонений  от
от  имеет определенную вероятность. При выборочном обследовании реальное значение
имеет определенную вероятность. При выборочном обследовании реальное значение  в ГС неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки
в ГС неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки  . Она определяется в долях средней ошибки с заданной вероятностью, т.е.
. Она определяется в долях средней ошибки с заданной вероятностью, т.е. = t
= t  , (67)
, (67) при
при 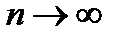 . (68)
. (68) , (69)
, (69) – нормированное отклонение выборочной средней от генеральной средней.
– нормированное отклонение выборочной средней от генеральной средней. или (
или ( –
–  )
) 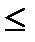

 (
( )(70)
)(70) или (
или ( –
–  +
+ 


