
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка соответствия ряда распределения закону ПуассонаСодержание книги
Поиск на нашем сайте
Таможенная инспекция провела проверку после выпуска товаров. В результате получен следующий дискретный ряд распределения числа нарушений, выявленных в каждой проверке (табл. 16). Таблица 16. Ряд распределения числа нарушений, выявленных таможенной инспекцией
Проведем анализ этого ряда распределения. Сначала рассчитаем среднее число нарушений в выборке, а также его дисперсию, для чего построим вспомогательную таблицу 17. Таблица 17. Ряд распределения числа нарушений, выявленных таможенной инспекцией
Среднее число нарушений в выборке по формуле (11): Дисперсию определим по формуле (28): Построив график этого распределения (полигон) – рис. 11, видно, что данное распределение не похоже на нормальное.
Рис. 11. Кривая распределения числа нарушений, выявленных таможенной инспекцией Из структурных характеристик ряда распределения можно определить только моду: Мо = 0, так как по данным табл. 17 такое число нарушений чаще всего встречается (f =24). По формуле (24) определим размах вариации: H = 3 – 0 = 3, что характеризует вариацию в 3 нарушения. По формуле (26) найдем среднее линейное отклонение:
Это означает, что в среднем число нарушений отклоняется от среднего их числа на 0,55. Среднее квадратическое отклонение рассчитаем не по формуле (28), а как корень из дисперсии, которая уже была рассчитана нами выше: Поскольку квартили на предыдущем этапе не определялись, на данном этапе расчет среднего квартильного расстояния пропускаем. Теперь рассчитаем относительные показатели вариации: – относительный размах вариации по формуле (32): – линейный коэффициент вариации по формуле (33): – квадратический коэффициент вариации по формуле(34): Все расчеты на данном этапе свидетельствуют о значительных размере и интенсивности вариации нарушений, выявленных таможенной инспекцией. Не имеет практического смысла расчет моментов распределения, так как видно из рис. 11, что в изучаемом распределении симметрия отсутствует вовсе, поэтому и расчет эксцесса также бесполезен. Выдвинем гипотезу о соответствии изучаемого распределения распределению Пуассона[26], которое описывается формулой (48):
где P(X) – вероятность того, что признак примет то или иное значение X; e = 2,7182 – основание натурального логарифма; X! – факториал числа X (т.е. произведение всех целых чисел от 1 до X включительно); a = Из формулы (48) видно, что единственным параметром распределения Пуассона является средняя арифметическая величина. Порядок определения теоретических частот этого распределения следующий: 1) рассчитать среднюю арифметическую ряда, т.е. = a; 2) рассчитать e – a ; 3) для каждого значения X рассчитать теоретическую частоту по формуле (49):
Поскольку a = m0 = m2 = Полученные теоретические частоты занесем в 5-й столбец табл. 17 и построим график эмпирического и теоретического распределений (рис. 12), из которого видна близость эмпирического и теоретического распределений.
Рис. 12. Эмпирическая и теоретическая (распределение Пуассона) кривые распределения Проверим выдвинутую гипотезу о соответствии изучаемого распределения закону Пуассона с помощью критериев согласия. Рассчитаем значение критерия Пирсона χ2 по формуле (44) в 6-м столбце табл. 17: χ2 =5,479, что меньше табличного (Приложение 3) значения χ2 табл=5,9915 при уровне значимости α = 0,05 и числе степеней свободы ν= 4–1–1=2, значит с вероятностью 0,95 можно говорить, что в основе эмпирического распределения лежит закон распределения Пуассона, т.е. выдвинутая гипотеза не отвергается, а расхождения объясняются случайными факторами. Определим значение критерия Романовского по формуле (46):
Для расчета критерия Колмогорова в последних трех столбцах таблицы 17 приведены расчеты накопленных частот и разностей между ними, откуда видно, что в 1-ой группе наблюдается максимальное расхождение (разность) D = 2,3. Тогда по формуле (47): 3.7. Контрольные задания На основе условных ранжированных данных таблицы 18 провести анализ вариации величины налоговых сборов (тыс. руб.) с предприятий района, собранных налоговыми органами. Таблица 18. Распределение вариантов для выполнения контрольного задания
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.199 (0.011 с.) |

 ) 2 f
) 2 f
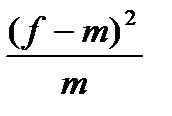
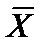 = 11/31 = 0,355 (нарушений).
= 11/31 = 0,355 (нарушений).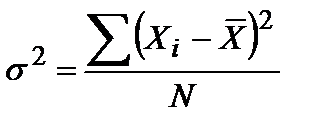 =
= 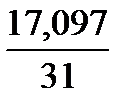 = 0,552 (нарушений2).
= 0,552 (нарушений2).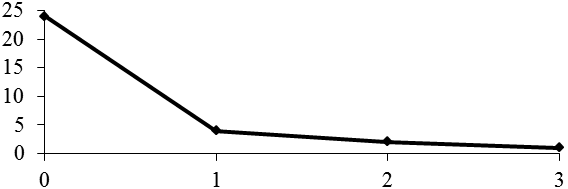
 .
.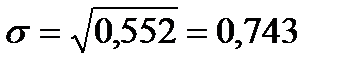 , тогда
, тогда 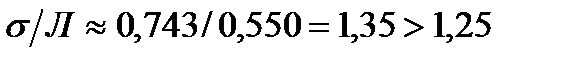 , т.е. в изучаемом распределении наблюдается некоторое число выделяющихся нарушений (с большим числом нарушений, выявленных в одной проверке).
, т.е. в изучаемом распределении наблюдается некоторое число выделяющихся нарушений (с большим числом нарушений, выявленных в одной проверке). = 3/0,355 = 8,45;
= 3/0,355 = 8,45;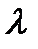 = 0,550/0,355 = 1,55;
= 0,550/0,355 = 1,55;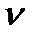 = 0,743/0,355 = 2,09.
= 0,743/0,355 = 2,09.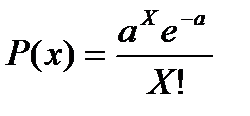 , (48)
, (48) – средняя арифметическая ряда распределения.
– средняя арифметическая ряда распределения. . (49)
. (49) = 0,355 найдем значение e – 0,355 =0,7012. Затем, подставив в формулу (49) значения X от 0 до 3, вычислим теоретические частоты:
= 0,355 найдем значение e – 0,355 =0,7012. Затем, подставив в формулу (49) значения X от 0 до 3, вычислим теоретические частоты: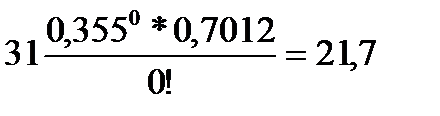 (т.к. 0! = 1); m1 =
(т.к. 0! = 1); m1 = 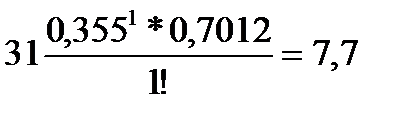 ;
;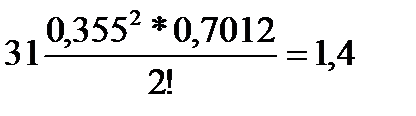 ; m3 =
; m3 = 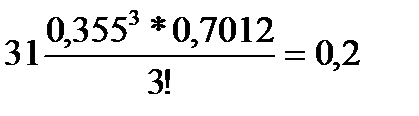 .
.
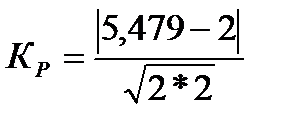 = 1,74 < 3, что подтверждает несущественность расхождений между эмпирическими и теоретическими частотами.
= 1,74 < 3, что подтверждает несущественность расхождений между эмпирическими и теоретическими частотами.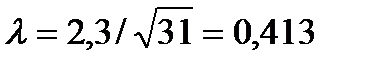 . По таблице Приложения 6 находим значение вероятности при λ = 0,4: P = 0,9972 (наиболее близкое значение к 0,413), т.е. с вероятностью, близкой к единице, можно говорить, что в основе эмпирического распределения величины нарушений, выявленных таможенной инспекцией, лежит закон распределения Пуассона, а расхождения эмпирического и теоретического распределений носят случайный характер.
. По таблице Приложения 6 находим значение вероятности при λ = 0,4: P = 0,9972 (наиболее близкое значение к 0,413), т.е. с вероятностью, близкой к единице, можно говорить, что в основе эмпирического распределения величины нарушений, выявленных таможенной инспекцией, лежит закон распределения Пуассона, а расхождения эмпирического и теоретического распределений носят случайный характер.


