
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Экономические индексыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве или сравнение фактических данных с любым эталоном (план, прогноз, норматив и т. д.). В международной практике индексы принято обозначать символами i и I (начальная буква латинского слова index). Буквой " i " обозначаются индивидуальные индексы, буквой " I " — общие индексы. Знак внизу справа означает период: 0 — базисный; 1 — отчетный. Помимо этого используются определенные символы для обозначения индексируемых показателей: q — количество (объем) какого-либо продукта в натуральном выражении; р — цена единицы товара; z — себестоимость единицы продукции; t — затраты времени на производство единицы продукции; w — выработка продукции в стоимостном выражении на одного рабочего или в единицу времени; v — выработка продукции в натуральном выражении на одного рабочего или в единицу времени; Т — общие затраты времени (tq) или численность рабочих; pq — стоимость продукции или товарооборот; zq — общие затраты на производство продукции. По степени охвата явления индексы бывают индивидуальные и сводные (общие). Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. Для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы (изменения: физического объема продукции, включающей разноименные товары, индекса цен акций предприятий региона и т. п.), рассчитывают сводные (общие) индексы. В зависимости от формы построения различаются индексы агрегатные и средние. Последние делятся на арифметические и гармонические. Агрегатная форма общих индексов является основной формой экономических индексов. Средние индексы — производные, они получаются в результате преобразования агрегатных индексов. По характеру объекта исследования общие индексы подразделяются на индексы количественных (объемных) и качественных показателей. В основе такого деления индексов лежит вид индексируемой величины. По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава. Деление индексов на эти две группы используется для анализа динамики средних показателей.
Индивидуальные индексы представляют собой относительные величины динамики, выполнения плана, сравнения, и их расчет не требует знания специальных правил. В зависимости от экономического назначения индивидуальные индексы бывают: физического объема продукции, себестоимости, цен, трудоемкости и т. д. Индекс физического объема продукции рассчитывается по формуле:
Индекс цены:
Индекс товарооборота (стоимости продукции):
Индексы других показателей строятся аналогично. Производительность труда может быть измерена количеством продукции, производимой в единицу времени (выработкой), или затратами рабочего времени на производство единицы продукции (трудоемкостью). Поэтому можно построить: • индекс производительности труда (через выработку):
• индекс производительности труда (через трудоемкость):
Так как между количеством продукции, произведенной в единицу времени, и затратами рабочего времени на производство единицы продукции существует обратно пропорциональная зависимость, т. е. t = 1/ V, то индекс it получается в результате деления величины показателя в базисном периоде на величину в текущем периоде. Для характеристики производительности труда часто используется индивидуальный индекс выработки продукции в стоимостном выражении на одного рабочего:
где p — сопоставимые цены. В экономических расчетах чаще всего используются сводные (общие) индексы, которые характеризуют изменение совокупности в целом. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов — агрегатная или средняя. Агрегатный индекс — сложный относительный показатель, который характеризует среднее изменение социально-экономического явления состоящего из несоизмеримых элементов. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной в числителе и знаменателе (вес индекса). Индексируемой величиной называется признак, изменение которого изучается (цена товаров, затраты времени, количество проданных товаров и т. д.). Вес индекса — это величина, служащая для целей соизмерения индексируемых величин.
Индекс стоимости продукции или товарооборота (Ipq) представляет собой отношение стоимости продукции текущего периода стоимости продукции в базисном периоде и определяется по формуле:
Значение индекса стоимости продукции (товарооборота) зависит от двух факторов: изменения количества продукции и цен, что обусловливает возможность и необходимость построения еще двух индексов: физического объема продукции и цен. Индекс физического объема продукции — это индекс количественного показателя. В этом индексе индексируемой величиной будет количество продукции в натуральном выражении, а весом – цена. Только умножив несоизмеримые между собой количества разнородной продукции на их цены, можно перейти к стоимостям продукции, которые будут уже величинами соизмеримыми. Так как индекс физического объема — индекс количественного показателя, то весами будут цены базисного периода. Тогда формула индекса примет следующий вид:
Индекс цен — это индекс качественного показателя. Индексируемой величиной будет цена товара, так как этот индекс характеризует изменение цен. Весом будет выступать количество произведенных товаров. Индекс цен Пааше определяется последующей формуле:
Если в этом индексе веса взять за базисный период, то получим индекс цен Ласпейреса:
Используя два этих индекса рассчитывают индекс цен Фишера:
Стоимость продукции можно представить как произведение количества товара на его цену. Такая же связь существует и между индексом стоимости, физического объема и цен, т. е.
Помимо агрегатных индексов в статистике применяется другая их форма — средневзвешенные индексы. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Средний индекс — это индекс, вычисленный как средняя величина из индивидуальных индексов. Агрегатный индекс является основной формой общего индекса, поэтому средний индекс должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая. Среднеарифметический индекс физического объема продукции вычисляется по формуле:
Среднеарифметический индекс цен Ласпейреса:
Среднегармонический индекс себестоимости можно исчислить так:
Среднегармонический индекс цен Пааше:
Пример 8.1: Имеются следующие данные
Определить: 1) Индивидуальные и сводные индексы цен и физического объема товарооборота. 2) Абсолютное изменение товарооборота за счет изменения цен; количества проданного товара; за счет цен и количества вместе. 3) Показать взаимосвязь 3 исчисленных сводных индексов. Решение: Определим индивидуальные индексы: По товару А i p = цены на товар А выросли в отчетном году на 27,3%; i q = объем продаж по товару А увеличился на 4,8%. По товару Б i p = цены на товар Б выросли в отчетном периоде на 15,2%; i q = товара Б было продано в отчетном периоде по сравнению с базисным на 13,3% меньше. Рассчитаем агрегатный индекс физического объема товарооборота, который будет характеризовать изменение объема продажи товаров. Сначала определим стоимость проданных товаров:
- в отчетном периоде в ценах базисного периода:
- в базисном периоде в ценах базисного периода:
Отношение стоимости товаров, проданных в отчетном периоде к стоимости товаров, проданных в базисном периоде дает агрегатный индекс физического объема товарооборота: I q = то есть объем продаж товаров в отчетном периоде по сравнению с базисным периодом снизился в целом на 7,6%. Разность между числителем и знаменателем индекса физического объема товарооборота дает прирост (или снижение) товарооборота в неизменных ценах: Δ pq(q) = Снижение товарооборота в абсолютной сумме в отчетном периоде за счет уменьшения количества проданного товара на 7,6% составило 550 тыс. руб. Рассчитаем сводный индекс цен. В качестве веса используем количество товаров отчетного периода (по формуле Пааше): I p = В целом цены на товары в отчетном периоде по сравнению с базисным периодом выросли на 19,5%. Разность между числителем и знаменателем индекса цен дает прирост (снижение) товарооборота за счет изменения цен: Δ pq(p) = Прирост товарооборота в абсолютной сумме в отчетном периоде составил 1310 тыс. рублей за счет увеличения цен на 19,5%. Рассчитаем агрегатный индекс товарооборота в фактических ценах: I pq = Товарооборот в фактических ценах вырос в отчетном периоде по сравнению с базисным периодом на 10,5%. Разность между числителем и знаменателем индекса товарооборота в фактических ценах дает прирост (или снижение) товарооборота в абсолютной сумме: Δ pq =
Произведение двух индексов ( Если посмотреть в абсолютной сумме изменение товарооборота, то очевидно, что за счет роста цен товарооборот увеличился на 1310 тыс. рублей, за счет снижения физического объема продаж уменьшился на 550 тыс. руб., а в целом за счет цен и количеств вырос на 770 тыс. рублей. (1310–550= 770) Пример 8.2: По данным примера 8.1
Определить общий индекс физического объема товарооборота.
Решение: q = то есть получили тот же количественный результат, что и у агрегатного индекса. Пример 8.3: По данным примера 8.1
Определить общий индекс цен. Решение: Воспользуемся среднегармоническим индексом цен: p = Получим тот же количественный результат, что и при расчете агрегатного индекса цен. Индексный метод применяется также для изучения динамики средних величин (средней цены на один и тот же товар, себестоимости) по однородной совокупности и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов. Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Например, индекс переменного состава средней себестоимости продукции одного и того же вида рассчитывается по формуле:
Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае себестоимости), но и структуры совокупности (весов). Индекс постоянного (фиксированного) состава — это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксированного состава определяется как агрегатный индекс. Так, индекс фиксированного состава средней себестоимости продукции рассчитывают по формуле:
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления. Индекс определяется по формуле (при изучении изменения среднего уровня себестоимости):
Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:
Между важнейшими индексами существуют взаимосвязи, позволяющие на основе одних индексов получить другие. Зная, например, значение цепных индексов (база – предыдущий период) за какой-либо период времени, можно рассчитать базисные индексы. И наоборот, если известны базисные индексы, то путем деления одного из них на другой можно получить цепные индексы. Пример 8.4. Цепные индексы цен за каждый месяц квартала составили 101%, 102,3%, 101,8%. Определить изменение цен за квартал. Решение: преобразуем индексы из процентов в коэффициенты и перемножим их. Получим базисный индекс, характеризующий рост цен за весь квартал Ip = 1,01 · 1,023 · 1,018 = 1,0518 или 105,18% Цены за квартал выросли на 5,18%. Пример 8.5. Цены в мае по сравнению с декабрем прошлого года выросли на 6,2%, а в июне — на 7,4%. Определить изменение цен в июне по сравнению с маем. Решение: преобразуем исходные данные в индексы. I 5 = 100+6,2 = 106,2%; I 6 = 100 + 7,4 = 107,4%. Эта два базисных индекса цен. За базу взяты цены декабря прошлого года. Для нахождения цепного индекса разделим базисные индексы I6/5 = 107,4 / 106,2 = 1,0113 или 101,13% Цены в июне по сравнению с маем выросли на 1,13% Существующие взаимосвязи между важнейшими индексами позволяют выявить влияние различных факторов на изменение изучаемого явления, например связь между индексом стоимости продукции, физического объема продукции и цен. Другие индексы также связаны между собой. Так, индекс затрат на производства — это произведение индекса себестоимости единицы продукции и индекса физического объема продукции:
Пример 8.6. Себестоимость единицы продукции увеличилась на 10%, а количество продукции снизилось на 8%. Определить изменение затрат на производство. Решение: выразим в виде индексов исходные данные. Iz = 110% или 1,10, Iq = 92% или 0,92 Индекс затрат на производство будет равен: Izq = 1,10 ´ 0,92 = 1,012, или 101,2%, или рост на 1,2% Пример 8.7. Физический объем производства продукции в текущем периоде вырос на 15%, трудоемкость единицы продукции снизилась на 7%. Определить изменение общих затрат времени на производство. Решение: индекс затрат времени (IT) на производство продукции может быть получен в результате умножения индекса физического объема продукции и индекса трудоемкости
Пример 8.8. Численность рабочих возросла на 12%, а производительность труда — на 7%. Определить индекс физического объема продукции. Решение: индекс физического объема продукции равен произведению индекса производительности труда на индекс затрат рабочего времени (или численности занятых):
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 933; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.143 (0.01 с.) |

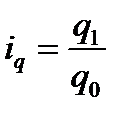
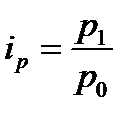
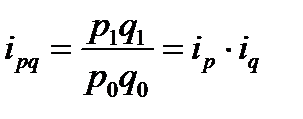
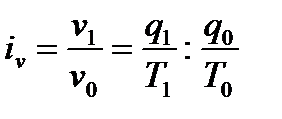
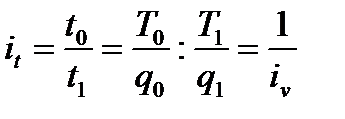
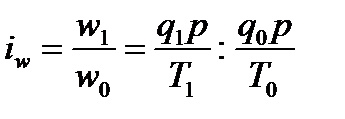
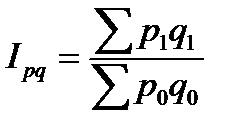
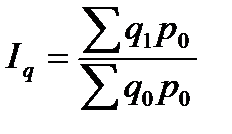
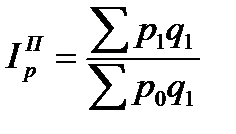
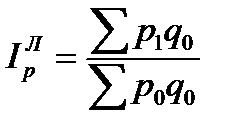
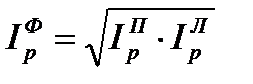
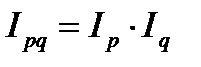
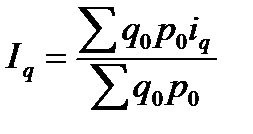
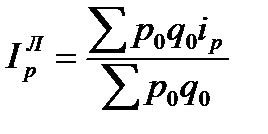
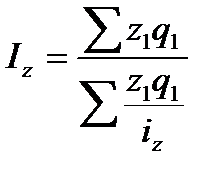
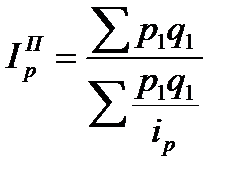
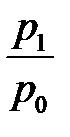 =
= 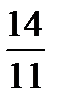 = 1,273 или 127,3%,
= 1,273 или 127,3%,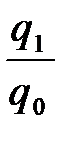 =
= 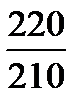 = 1,048 или 104,8%,
= 1,048 или 104,8%, =
= 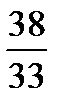 = 1,152 или 115,2%,
= 1,152 или 115,2%,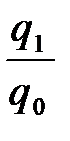 =
= 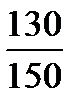 = 0,867 или 86,7%,
= 0,867 или 86,7%,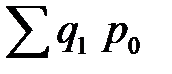 = 220·11+ 130·33= 6710 (тыс. руб.),
= 220·11+ 130·33= 6710 (тыс. руб.),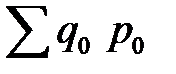 = 210·11 + 150·33 = 7260 (тыс. руб.).
= 210·11 + 150·33 = 7260 (тыс. руб.).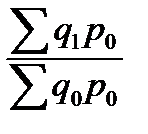 =
= 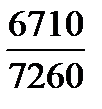 = 0,924 или 92,4%,
= 0,924 или 92,4%,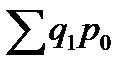 –
– 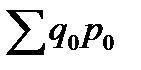 = 6710 – 7260 = –550 (тыс. руб.).
= 6710 – 7260 = –550 (тыс. руб.).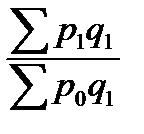 =
= 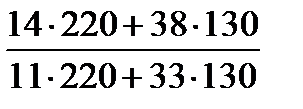 =
= 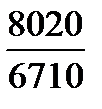 = 1,195 или 119,5%.
= 1,195 или 119,5%.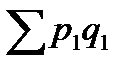 –
– 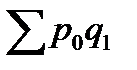 = 8020 – 6710 = 1310 (тыс. руб.).
= 8020 – 6710 = 1310 (тыс. руб.).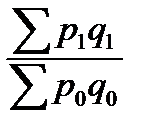 =
= 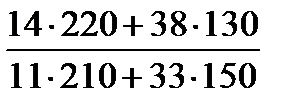 =
= 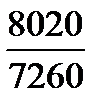 = 1,105 или 110,5%.
= 1,105 или 110,5%.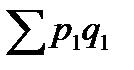 –
– 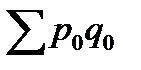 = 8020 – 7260 = 760 (тыс. руб.).
= 8020 – 7260 = 760 (тыс. руб.).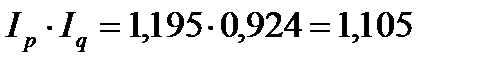 ) дает нам показатель динамики товарооборота в фактических ценах (I pq), то есть за счет роста цен на 19,5% и снижения физического объема продаж на 7,6%, товарооборот увеличился в отчетном году на 10,5%.
) дает нам показатель динамики товарооборота в фактических ценах (I pq), то есть за счет роста цен на 19,5% и снижения физического объема продаж на 7,6%, товарооборот увеличился в отчетном году на 10,5%.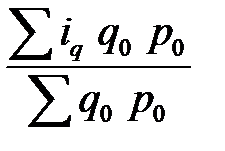 =
= 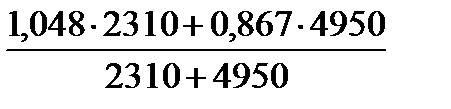 =
= 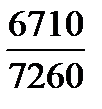 = 0,924 или 92,4%,
= 0,924 или 92,4%,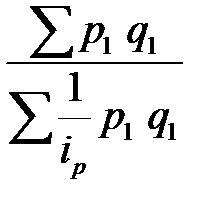 =
= 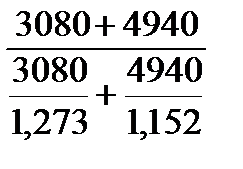 =
= 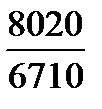 = 1,195 или 119,5%.
= 1,195 или 119,5%.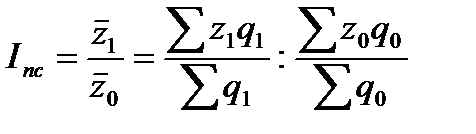 .
.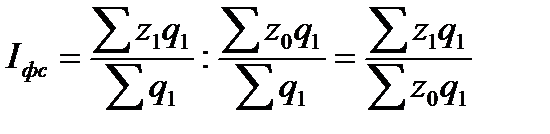 .
.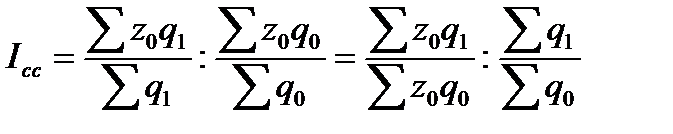 .
.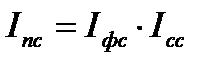
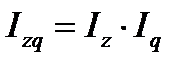
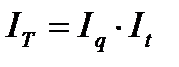 = 1,15 · 0,93 = 1,0695, или 106,95%, или увеличение на 6,95%.
= 1,15 · 0,93 = 1,0695, или 106,95%, или увеличение на 6,95%.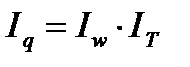 = 1,12 · 1,07 = 1,1984, или 119,84%.
= 1,12 · 1,07 = 1,1984, или 119,84%.


