
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выравнивание по уравнению прямойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение прямой может быть выражено в виде следующей формулы: yt =ao+a 1 t, где yt – значение выровненного ряда; ao, a 1 – параметры прямой линии (которые необходимо вычислить); t – показатель времени. Задача состоит в том, чтобы фактические уровни ряда (у) заменить теоретическими (yt). Для расчета параметров прямой линии ao и a 1 используем способ наименьших квадратов, который дает систему двух уравнений:
где n – число членов ряда; у – фактические уровни ряда; t – показатель времени. Упрощенный расчет параметров уравнений заключается в переносе начала координат в середину ряда динамики (S t =0). В этом случае упрощаются сами нормальные уравнения, кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. Тогда системы нормальных уравнений для оценивания параметров прямой (у = a0+a1t) примут вид:
Решая систему относительно неизвестных параметров, получим величины параметров соответствующих полиномов. Пример 7.7. Пример. Имеются данные о продажах по месяцам.
Решение. Составим рабочую таблицу для расчета параметров уравнения прямой
Уравнение тренда yt = 18,0 + 1,321· t Построим график фактических уровней и линию, характеризующую тенденцию динамического ряда.
Методы выявления сезонной компоненты При рассмотрении квартальных или месячных данных многих социально-экономических явлений часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также ряда многочисленных разнообразных факторов, которые частично являются регулируемыми. В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезонных колебаний» или «сезонных волн», а динамический ряд в этом случае называют тренд-сезонным, или просто сезонным рядом динамики. Сезонные колебания характеризуются специальными показателями которые называются индексами сезонности (IS). Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней. Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Данные за несколько лет (не менее трех) используются для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года. Для вычисления индексов сезонности применяются различные методы. Если ряд динамики не содержит явно выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания. Для каждого месяца рассчитывается средняя величина уровня, например, за три года (
Если же ряд динамики содержит определенную тенденцию в развитии, то прежде чем вычислить сезонную волну, фактические данные должны быть обработаны так, чтобы была выявлена общая тенденция. Обычно для этого прибегают к аналитическому выравниванию ряда динамики. По уравнению вычисляются для каждого месяца (квартала) выравненные уровни на момент времени t (
И находят средние арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах: IS=(I1+I2+…+In): n, где n — число одноименных периодов (месяцев, кварталов). В общем виде формулу расчета индекса сезонности данным способом можно записать так:
Основы прогнозирования Исследование динамики социально-экономических явлений, выявление и характеристика основной тенденции развития и моделей взаимосвязи дают основание для прогнозирования — определения будущих размеров уровня экономического явления. Выделяют следующие элементарные методы прогнозирования: по среднему абсолютному приросту, по среднему темпу роста и на основе выравнивания рядов по какой-либо аналитической формуле. Прогнозирование по среднему абсолютному приросту (
где n — номер последнего уровня исследуемого периода, за который рассчитан`D; i — срок прогноза (период упреждения). Прогнозирование по среднему темпу роста осуществляется в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста (
где уn — последний уровень ряда динамики; i — срок прогноза; Наиболее распространенным методом прогнозирования считают аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t). При таком подходе к прогнозированию предполагается, что размер уровня, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, т. е. у = f(t). При выборе типа линии можно учитывать следующее: - прямая линия — если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины; - парабола второго порядка (полином) — если приросты приростов уровней (ускорения) колеблются около постоянной величины; - показательная функция (экспонента) — если уровни изменяются с приблизительно постоянным относительным приростом. Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, имеет малую вероятность. Любой статистический прогноз носит приближенный характер. Поэтому целесообразно определение доверительных интервалов прогноза. Точечный прогноз на k шагов вперед получается путем подстановки в модель параметра t=n +1, …, n + k. Доверительный интервал прогноза будет иметь следующие границы: верхняя граница прогноза = yp(n+k) + U(k), нижняя граница прогноза = yp(n+k) – U(k). Величина U(k) для линейной модели имеет следующий вид:
где sy — средняя квадратическая ошибка тренда; yp — расчетное значение уровня (по уравнению); m — число параметров уравнения (для линейного m = 2); n — количество исходных уровней; ` t — среднее значение параметра t (для имеющихся данных); k p — доверительная величина, определяемая на основе t -критерия Стьюдента.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.007 с.) |

 ;
; .
. 126 / 7 = 18,0 a 1=
126 / 7 = 18,0 a 1= 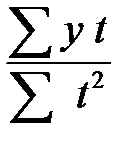 =37/ 28 = 1,321
=37/ 28 = 1,321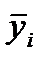 ), затем из них вычисляется среднемесячный уровень для всего ряда
), затем из них вычисляется среднемесячный уровень для всего ряда  и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, т. е.
и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, т. е. .
. ). Затем определяются отношения фактических данных за месяц (квартал) к соответствующим выравненным данным:
). Затем определяются отношения фактических данных за месяц (квартал) к соответствующим выравненным данным:

 ) — основано на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов). Экстраполяцию можно сделать по следующей формуле:
) — основано на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов). Экстраполяцию можно сделать по следующей формуле: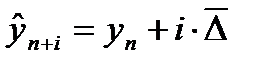
 — экстраполируемый уровень; (n+i) — номер этого уровня;
— экстраполируемый уровень; (n+i) — номер этого уровня; ), возведенный в степень, соответствующую периоду экстраполяции, т. е. по формуле:
), возведенный в степень, соответствующую периоду экстраполяции, т. е. по формуле:





