
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол между прямой и плоскостью.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из определения следует, что угол между прямой и плоскостью не превышает Пусть Через
Но
38) Условие перпендикулярности прямой и плоскости -
39) Расстояние от точки до прямой в пространстве- Расстоянием от точки до прямой в пространстве называется длина перпендикуляра, опущенного из данной точки на прямую.
40) Кратчайшее расстояние между двумя прямыми в пространстве. -
41) Уравнение плоскости, проходящей через точку и прямую – A(x-x1)+B(y-y1)+C(z-z1)=0 42) Уравнение плоскости, проходящей через две пересекающиеся прямые
Если
43) Уравнение плоскости, проходящей через две параллельные прямые
Если прямые заданы соответственно уравнениями:
то уравнение плоскости есть
44) Уравнение плоскости, проходящей через точку перпендикулярно данной прямой – A1(x - x0) + B1(y - y0) + C1(z - z0) = 0 45)Уравнение прямой, проходящей через данную точку перпендикулярно 46)Определение эллипса(1), вывод канонического уравнения(2). Свойства эллипса(3) – (1)Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная. (2) Введем систему координат: Пусть
Запишем характеристическое уравнение эллипса в координатной форме:
Преобразуем равенство:
Перенесем в левую часть равенства выражение, содержащее корень:
Так как
(3) -Эллипс пересекает каждую из осей координат в двух точках. - Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси. - Эллипс имеет две взаимно перпендикулярные оси симметрии. - Эллипс имеет центр симметрии. - Эллипс может быть получен сжатием окружности 47) Определение гиперболы(1), вывод канонического уравнения(2). Свойства гиперболы(3) – (1) Гиперболой называется геометрическое место точек в плоскости, абсолютная величина разности расстояний, каждое из которых от двух данных точек этой плоскости, называемых фокусами есть величина постоянная, отличная от ноля. (2) Воспользовавшись формулой расстояния между двумя точками и проведя процедуру избавления от иррациональности, будем иметь:
Если ввести обозначение b 2 = c 2 − a 2, то уравнение гиперболы примет вид x 2· b 2 − a 2· y 2 = a 2 b 2. Выполнив преобразование, аналогичное выводу уравнения эллипса, получим каноническое уравнение гиперболы:
(3) - Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (– a; 0), которые называются вершинами гиперболы. - Гипербола имеет две взаимно перпендикулярные оси симметрии. - Гипербола имеет центр симметрии.(Центр симметрии гиперболы называют центром гиперболы.) - Гипербола пересекается с прямой y = kx при
48) Эксцентриситет и директрисы эллипса и гиперболы – Директрисами эллипса называются прямые, параллельные малой оси эллипса и отстоящие от неё на расстояние a/e, где e – эксцентриситет эллипса. Очевидно, что директрисы не пересекают эллипс, так как e<1 и a/e>a.
Замечание. Окружность не имеет директрис.
Директрисами гиперболы называются прямые, параллельные оси Oy и отстоящие от неё на расстояние a/e, где e – эксцентриситет гиперболы. Существует две директрисы: d1 – соответствующая фокусуv F1 и d2 – соответствующая фокусу F2.
49) Определение параболы(1), вывод канонического уравнения(2). Свойства параболы(3) – (1) Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой. (2) Для вывода уравнения параболы введем на плоскости прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус перпендикулярно директрисе, и будем считать ее положительным направлением направление от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой. Выведем уравнение параболы в выбранной системе координат.
Через d – расстояние от точки до директрисы, а через р расстояние от фокуса до директрисы. Величину называют параметром параболы, его геометрический смысл раскрыт далее. Точка М будет лежать на данной параболе в том и только в том случае, когда r = d.
Далее избавимся от иррациональности
Уравнение y 2 = 2 p x называется каноническим уравнением параболы. (3) - Парабола имеет ось симметрии. - Парабола расположена в полуплоскости x ≥ 0.
50) Цилиндры. Примеры – Цилиндр — геометрическое тело, ограниченной цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра); причём если оснований два, то одно получено из другого параллельным переносом вдоль образующей боковой поверхности цилиндра; и основание пересекает каждую образующую боковой поверхности ровно один раз. Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется бесконечным цилиндром. Бесконечное тело, ограниченное замкнутым цилиндрическим лучом и его основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ОПРЕДЕЛЕНИЕ. Углом между прямой
ОПРЕДЕЛЕНИЕ. Углом между прямой  и плоскостью
и плоскостью  называется угол
называется угол  между прямой
между прямой  , т.е. угол острый.
, т.е. угол острый.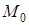 – их точка пересечения.
– их точка пересечения. . Для
. Для  является направляющим и, следовательно, острый угол
является направляющим и, следовательно, острый угол  между прямыми
между прямыми 
 .
. ,
,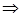


 |M1M0×a|=|M1M0|•|a|•sinφ. sinφ=d/|M1M0|, следовательно, d=|M1M0|•sinφ. Тогда в силу первого равенства |M1M0×a|=d•|a|. d=|M1M0×a|/|a|. Так как относительно ПДСК вектор M1M0={x0-x1, y0-y1, z0-z1}, a={a, b, c}, то
|M1M0×a|=|M1M0|•|a|•sinφ. sinφ=d/|M1M0|, следовательно, d=|M1M0|•sinφ. Тогда в силу первого равенства |M1M0×a|=d•|a|. d=|M1M0×a|/|a|. Так как относительно ПДСК вектор M1M0={x0-x1, y0-y1, z0-z1}, a={a, b, c}, то


 и
и  :
: или
или 
 , то уравнение плоскости есть
, то уравнение плоскости есть
 и
и 

 и
и 


 Обозначим фокусы эллипса буквами
Обозначим фокусы эллипса буквами  и
и  . Расстояние между ними - фокальное расстояние
. Расстояние между ними - фокальное расстояние  ,
,  и
и 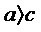 . Если
. Если  - произвольная точка эллипса, то по определению эллипса
- произвольная точка эллипса, то по определению эллипса  - характеристическое уравнение эллипса.
- характеристическое уравнение эллипса. ,
,  и
и  . Тогда фокусами будут точки
. Тогда фокусами будут точки  и
и  .
.











 . Пусть
. Пусть  , то
, то - каноническое уравнение эллипса.
- каноническое уравнение эллипса.

 в двух точках. Если
в двух точках. Если  то общих точек у прямой и гиперболы нет.
то общих точек у прямой и гиперболы нет.







