
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному вектору. Пусть плоскость задана точкой M0(x0;y0;z0) и вектором Возьмем произвольную точку M(x;y;z) и составим вектор
Общее уравнение плоскости.
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0) · Если С=0 то вектор · Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz. Аналогично при A=D=0 и B=D=0. · Если А=В=0 то уравнение примет вид · Если A=B=D=0, то уравнение имеет вид Уравнение плоскости, проходящей через три точки К (х1;у1) М (х2;у2) N (x3;y3) Возьмем на плоскости точку P (x;y;z). Составим векторы:
Эти векторы лежат в одной плоскости, следовательно они компланарны:
Уравнение плоскости в отрезках. Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
Нормальное уравнение плоскости.
Угол между прямой и плоскостью. Расстояние от точки до плоскости.
Прямая L: Пусть φ – угол между плоскостью и прямой. Тогда θ – угол между
Найдем
Расстояние от точки до плоскости. Дано: M0 (x0;y0;z0)
Расстояние d от точки М0 до плоскости ∆ равно модулю проекции вектора
!!!Если плоскость задана уравнением:
то расстояние до плоскости находится по формуле:
Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между двумя прямыми. Уравнение с угловым коэффициентом.
k= tg α – угловой коэффициент. Если b=0 то прямая проходит через начало координат. Уравнение примет вид Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох. Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет вид Общее уравнение прямой.
A, B, C – произвольные числа, причем А и В не равны нулю одновременно. · Если В=0, то уравнение имеет вид · Если В≠0, то получаем уравнение с угловым коэффициентом · Если А=0, то уравнение имеет вид · Если С=0, то уравнение проходит через т. О (0;0). Уравнение прямой, проходящей через точку, в данном направлении. т М (х0;у0). Уравнение прямой записывается в виде Подставим в это уравнение точку М Решим систему:
Уравнение прямой, проходящей через 2 точки. К (х1;у1) М (х2;у2)
Уравнение прямой в отрезках. К (а;0); М (0;b) Подставим точки в уравнение прямой:
Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору. М0 (х0;у0). Возьмем произвольную точку М (х;у).
Т.к.
Нормальное уравнение прямой. Уравнение прямой можно записать в виде:
Т.к.
Угол между прямыми. Дано: прямые L1 и L2 с угловыми коэффициентами
Требуется найти угол между прямыми:
Эллипс. Определение. Вывод канонического уравнения.
геометрическое место всех точек плоскости, сумма расстояний от которых до до фокусов есть величина постоянная, большая, чем расстояние между фокусами. Пусть М (х;у) – произвольная точка эллипса. Т.к. MF1 + MF2 = 2a
Т.к. То получаем Или
Гипербола. Определение. Вывод канонического уравнения. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная. Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1 – MF2|=2a или MF1 – MF2=±2a,
Парабола. Определение. Вывод канонического уравнения. Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0.
точка M с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению MF=MN.
Поверхности вращения. Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнение этой кривой запишутся в виде:
Возьмем на поверхности точку M (x;y;z). Проведем через точку М плоскость, перпендикулярную оси oz, и обозначим точки пересечения ее с осью oz и кривой L соответственно O1 и N. Обозначим координаты точки N (0;y1;z1). Отрезки O1M и O1N являются радиусами одной и той же окружности. Поэтому O1M = O1N. Но O1M = (x2+y2)0.5, O1N=|y1|. Следовательно, |y1|=(x2+y2)0.5 или y1=±(x2+y2)0.5. Кроме того, очевидно, z1=z. Следовательно
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.24.238 (0.007 с.) |

 , перпендикулярной этой плоскости.
, перпендикулярной этой плоскости. . При любом расположении точки М на плоскости Q
. При любом расположении точки М на плоскости Q  , поэтому
, поэтому  .
.
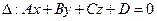
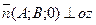 . Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox. плоскость параллельна плоскости Oxy.
плоскость параллельна плоскости Oxy. . Это уравнение плоскости Oxy.
. Это уравнение плоскости Oxy.

 ;
;  ;
; 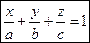


 .
.

 , если
, если 
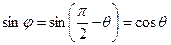 , т.к.
, т.к. 

 (где М1(x1;y1;z1) - произвольная точка плоскости) на направление нормального вектора
(где М1(x1;y1;z1) - произвольная точка плоскости) на направление нормального вектора 







 и пройдет параллельно оси оу.
и пройдет параллельно оси оу.
 или
или  . Это уравнение прямой, параллельной оси оу. и проходящей через точку
. Это уравнение прямой, параллельной оси оу. и проходящей через точку 
 .
. . Это уравнение прямой, параллельной оси ох.
. Это уравнение прямой, параллельной оси ох.

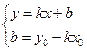



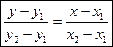






 ;
;  , то:
, то:



 Эллипсом называется
Эллипсом называется

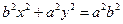

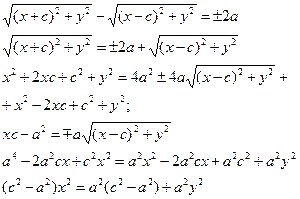


 Пусть M(x;y) – произвольная
Пусть M(x;y) – произвольная


 Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.
Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz. – искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на поверхности вращения.
– искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на поверхности вращения.


