
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть заданы точки должны быть компланарны, т.е.
Уравнение плоскости: Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости. Пусть заданы два вектора Уравнение плоскости: Уравнение плоскости по точке и вектору нормали. Теорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали Уравнение плоскости в отрезках. Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D)
Уравнение плоскости в векторной форме.
В координатах это уравнение имеет вид: xcos+ ycos+ zcos- p = 0. Нормальное уравнение плоскости. Обозначим через расстояние от начала координат до плоскости , а через
Последнее уравнение называется нормальным (нормированным) уравнением плоскости.
Нормальное уравнение плоскости. Обозначим через p расстояние от начала координат до плоскости П, а через Точка Q – проекция точки на ось, определяемую вектором Очевидно, точка лежит на рассматриваемой плоскости тогда и только тогда, когда проекция вектора на ось, определяемую вектором Так как Из данных равенств следует, что точка лежит на плоскости тогда и только тогда, когда координаты этой точки удовлетворяют уравнению xcos Последнее уравнение называется нормальным (нормированным) уравнением плоскости. Признаки расположения плоскости относительно прям.декартовой ск
т.О (0;0;0)∊ А) Cz+D=0 – ур-ие плоскости ||Oxy Б) А)
Ax+D=0 Б) А) By+D=0 Б)
Ox
Oy ∊
Oz ∊
Угол между плоскостями. Взаимное расположение двух плоскостей
Таким образом: Условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, что-бы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:
29. Различные виды уравнений прямой в пространстве. Дана прямая m, такая что
Замечание. Рассмотрим каноническое уравнение прямой в пространстве: А) а=о ⇒ Б) b=0⇒ В) с=0⇒
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2765; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.74 (0.011 с.) |

 ,
, 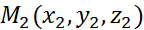 и вектор
и вектор  .Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору a. Векторы
.Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору a. Векторы 
 и вектор
и вектор 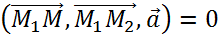

 , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы а,b,
, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы а,b,  должны быть компланарны.
должны быть компланарны.
 имеет вид:
имеет вид: 
 , заменив
, заменив 

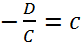 получим уравнение плоскости в отрезках:
получим уравнение плоскости в отрезках:  Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у,z.
Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у,z. ,где
,где  - радиус- вектор текущей точки М(х, у, z),
- радиус- вектор текущей точки М(х, у, z),  - единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат, , и - углы, образованные этим вектором с осями х, у, z, p – длина этого перпендикуляра.
- единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат, , и - углы, образованные этим вектором с осями х, у, z, p – длина этого перпендикуляра. единичный вектор нормали к этой плоскости
единичный вектор нормали к этой плоскости  , ,,– углы между n0 и положительным направлением координатных осей Ox, Oy, Oz Точка
, ,,– углы между n0 и положительным направлением координатных осей Ox, Oy, Oz Точка  является основанием перпендикуляра, опущенного из начала координат на . Точка Q – проекция точки M на ось, определяемую вектором n0. Очевидно, точка M (x, y, z) лежит на рассматриваемой плоскости тогда и только тогда, когда проекция вектора
является основанием перпендикуляра, опущенного из начала координат на . Точка Q – проекция точки M на ось, определяемую вектором n0. Очевидно, точка M (x, y, z) лежит на рассматриваемой плоскости тогда и только тогда, когда проекция вектора  на ось, определяемую вектором n0, равна p, т.е. при условии
на ось, определяемую вектором n0, равна p, т.е. при условии =p Так как n0– единичный вектор, то в силу определения скалярного произведения
=p Так как n0– единичный вектор, то в силу определения скалярного произведения  +y
+y  .Из данных равенств следует, что точка M (x, y, z) лежит на плоскости П тогда и только тогда, когда координаты этой точки удовлетворяют уравнению x cos y cos z cos p 0.
.Из данных равенств следует, что точка M (x, y, z) лежит на плоскости П тогда и только тогда, когда координаты этой точки удовлетворяют уравнению x cos y cos z cos p 0. единичный вектор нормали к этой плоскости (
единичный вектор нормали к этой плоскости ( – углы между
– углы между  и положительным направлением координатных осей Ox,Oy,Oz). Точка
и положительным направлением координатных осей Ox,Oy,Oz). Точка  является основанием перпендикуляра, опущенного из начала координат на П.
является основанием перпендикуляра, опущенного из начала координат на П. .
.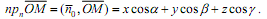
 + ycos
+ ycos  + zcos
+ zcos 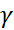 - p = 0.
- p = 0. . Oxyz – прямоуг.декартова ск.
. Oxyz – прямоуг.декартова ск.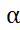 ⇒ D=0.
⇒ D=0. ||Oxy (z=0)⇒
||Oxy (z=0)⇒  ⇒ (
⇒ ( . (
. ( =0⇒B=0
=0⇒B=0 ,
,  ⇒ (
⇒ ( =0⇒C=0
=0⇒C=0 ,
,  ⇒ D=0 By+Cz=0
⇒ D=0 By+Cz=0 ⇒ (
⇒ ( ⇒Ax+Cz+D=0
⇒Ax+Cz+D=0
 ⇒ (
⇒ (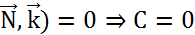 ⇒Ax+By+D=0
⇒Ax+By+D=0 Даны уравнения двух плоскостей:
Даны уравнения двух плоскостей: 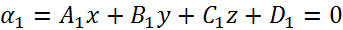 и
и  . Вектора нормали:
. Вектора нормали:  и
и  .
.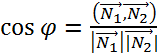 .
. ⇒
⇒  ⇒
⇒  =0
=0  .
. .
. 

 . Плоскости параллельны, векторы нормалей коллинеарны:
. Плоскости параллельны, векторы нормалей коллинеарны:  ||
||  .Это условие выполняется, если:
.Это условие выполняется, если:  ∊m,
∊m,  m (
m (  -направляющий вектор прямой)
-направляющий вектор прямой) .
.  .
.  - векторное уравнение прямой в пространстве.
- векторное уравнение прямой в пространстве. – параметрическое уравнение прямой в пространстве⇒
– параметрическое уравнение прямой в пространстве⇒ 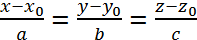 - каноническое уравнение прямой в пространстве.
- каноническое уравнение прямой в пространстве. ∊m.
∊m. 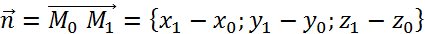
 - -через две точки.
- -через две точки.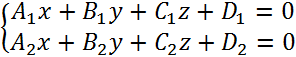 - общее уравнение прямой в пространстве.
- общее уравнение прямой в пространстве. ;
; ;
;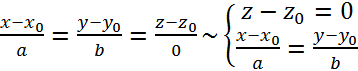 ;
;


