
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие об ориентации плоскости и пространства. Векторное произведение двух векторов и его основные свойства. Площадь параллелограмма.
Два базиса а1..., аn и b1,..., bn на плоскости (n = 2) или в пространстве (n = 3) называются одноименными, если определитель |С| матрицы перехода С от первого базиса ко второму положителен: |С | > 0. Если |С|>0, то базисы называются разноименными. Oтношение одноименности базисов является отношением эквивалентности. Поскольку отношение одноименности является отношением эквивалентности, все базисы разбиваются на классы одноименных базисов. Классы одноименных базисов называются ориентациями (соответственно — прямой, плоскости и пространства). На прямой, на плоскости и в пространстве существует точно две различные ориентации: базисы, принадлежащие одной и той же ориентации, одноименны, а базисы, принадлежащие различным ориентациям, разноименны. Прямая, плоскость или пространство, для которой (ого) выбрана некоторая ориентация, называется ориентированной (ым). Для каждой ориентации о другая возможная ориентация обозначается символом — о и называется противоположной ориентацией. О базисе, принадлежащем некоторой ориентации, говорят, что он определяет эту ориентацию. Базис ориентированной (ого) прямой, плоскости или пространства, определяющий данную ориентацию, называется положительно ориентированным (по отношению к данной ориентации), а базис, определяющий противоположную ориентацию, называется отрицательно ориентированным. Тройка некомпланарных векторов называется право ориентированной (правой), если после приложения трех векторов к одной точке кратчайший поворот от первого ко второму вектору виден из конца третьего вектора против часовой стрелки, в противном случае – лево ориентированная (левая). Есть и ещё один способ разделить эти два класса: Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая. Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададим ориентацию пространства. Для задания ориентации плоскости достаточно задать ориентации двух не параллельных прямых этой плоскости.
Для любой ориентации о плоскости и любой ориентации о2 прямой а2 существует такая ориентация о1 прямой Для задания ориентации пространства достаточно задать ориентации произвольной прямой и произвольной не параллельной ей плоскости. Векторное произведение двух векторов и его основные свойства. Векторным произведением вектора длина вектора вектор вектор Обозначение:
Геометрические свойства: 1.Если векторы а и b коллинеарны, то их векторное произведение равно нулю. 2. Если векторное произведение векторов а и b равно нулю, то векторы а и b коллинеарны. 3. Если векторы а и b приведены к общему началу, то модуль векторного произведения [a,b] равен площади параллелограмма, построенного на векторах а и b, как на сторанах. Док-во: Обозначим площадь параллелограмма, построенного на векторах а и b, буквой S. Как известно из элементарной геометрии, площадь параллелограмма равна произведению его смежных сторон на синус угла между ними. Отсюда |a||b|sin Алгебраические свойства: 1.Векторное произведение а и b есть вектор, обратный векторному произведению b и а. 2.[( 3.[a(b+c)]=[ab]+[ac] Выражение векторного произведения двух векторов через координаты векторов в правом ортонормированном базисе. Если векторы а и b заданы своими координатами: а={a1,a2,a3} b={b1,b2,b3} то векторное произведение вектора а на вектор b определяется формулой [ab]= {|
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 878; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.154.103 (0.008 с.) |
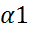 что О = 0102.
что О = 0102. на вектор
на вектор  в пространстве
в пространстве  называется вектор
называется вектор  , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям: между ними:
между ними:  ;
; направлен так, что тройка векторов
направлен так, что тройка векторов  является правой;
является правой;
 =S, следовательно |[a,b]|=S.
=S, следовательно |[a,b]|=S. a)b]=
a)b]= 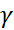 [ab]
[ab] |,-|
|,-|  |,|
|,|  |}
|}


