
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Биссектрисы углов между прямыми.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения биссектрис углов между прямыми Ах + By +С = 0 к Dx + Ey + F = 0:
18.Экстцентриситет эллипса. Рациональное выражение фокальных радиусов эллипса .Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; требуется, чтобы эта постоянная была больше расстояния между фокусами. Фокусы эллипса принято обозначать через F1 и F2.Замечание. Сумма расстояний произвольной точки М от двух фиксированных точек F1 и F2очевидно, не может быть меньше расстояния между точками F1, F2. Эта сумма равна расстоянию между F1 и F2в том и только в том случае, когда точка М находится на отрезке F1F2. Следовательно, геометрическое место точек, сумма расстояний от которых до двух фиксированных точек F1 и F2, есть постоянная величина, равная расстоянию между F1 и F2, представляет собой просто отрезок F1F2. Пусть М—произвольная точка эллипса с фокусами F1 и F2. Отрезки F1M и F2M (также как и длины этих отрезков) называются фокальными радиусами точки М. Постоянную сумму фокальных радиусов точки эллипса принято обозначать через 2а. Таким образом, для любой точки М эллипса имеем:F1M + F2M = 2 a. Расстояние F1F2 между фокусами обозначают через 2 с. Так как F1M + F2M > F1F2,то2 а > 2 с, т. е. а > с Так как с < а, то е < 1, т. е. эксцентриситет каждого эллипса меньше единицы. 19.Гипербола.Вывод канонического уравнения гиперболы. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению; кроме того, требуется,чтобы она была меньше расстояния между фокусами и отлична от нуля. Фокусы гиперболы принято обозначать через F1 и F2,а расстояние между ними — через 2 с. Замечание. Разность расстояний от произвольной точки М до двух фиксированных точек F1 и F2, очевидно, не может быть больше расстояния между точками F1 и F2. Эта разность равна расстоянию между F1F2в том и только в том случае, когда точка М находится на одном из продолжений отрезка F1F2.Следовательно, геометрическое место точек, для которых разность расстояний от двух фиксированных точек F1 и F2 есть постоянная величина, равная расстоянию между F1 и F2, представляет собой оба продолжения отрезка F1F2.Если разность расстояний от некоторой точки М до точек F1 и F2равна нулю, то эта точка равноудалена от F1 и F2. Следовательно, геометрическое место точек, разность расстояний от которых до двух фиксированных точек F1 и F2 есть постоянная величина, равная нулю, представляет собой прямую, перпендикулярную к отрезку F1F2 в его середине.Указанные случаи исключены оговоркой в конце предыдущего определения.Пусть М—произвольная точка гиперболы с фокусами F1 и F2 (см. рис.). Отрезки F1M и F2M (так же, как и длины этих отрезков) называются фокальными радиусами точки М и обозначаются через r 1 и r 2. По определению гиперболы разность фокальных радиусов ее точки М сть постоянная величина (т. е. при изменении положения точки М на гиперболе разность ее фокальных радиусов не меняется); эту постоянную принято обозначать через 2 а. Таким образом, для любой точки М гиперболы имеем
Так как по определению гиперболы F1M + F2M =2 a. Расстояние F1F2 между фокусами обозначают через 2 с. Так как F1M + F2M < F1F2,то2 а < 2 с, т. е. а < с. Далее увидим, что гипербола состоит из двух отдельных частей, называемых ее ветвями, каждая из которых бесконечно простирается в двух направлениях; целая гипербола симметрична относительно прямой F1F2, а также относительно прямой, проходящей перпендикулярно к отрезку F1F2 через его середину Пусть дана какая-нибудь гипербола с фокусами F1 и F2 (вместе с тем будем считать данными а и с). Введем на плоскости декартову прямоугольную систему координат, оси которой расположим специальным образом по отношению к этой гиперболе; именно, в качестве оси абсцисс мы возьмем прямую F1F2, считая ее направленной от F1 к F2, начало координат поместим в середину отрезка F1F2. Выведем уравнение гиперболы в установленной системе координат. Возьмем на плоскости произвольную точку М. Точка М будет находиться на (данной) гиперболе в томи только в том случае, когда Чтобы получить искомое уравнение гиперболы, нужно заменить переменные r 1 и r 2 их выражениями через текущие координаты x:, у. Так как F1F2 = 2 c и так как фокусы F1F2 расположены на оси Ох симметрично относительно начала координат, то они имеют соответственно координаты (- с; 0) и (с; 0); приняв это во внимание, находим: Тогда получаем: Это и есть уравнение рассматриваемой гиперболы в назначенной системе координат, так как ему удовлетворяют координаты точки М(х;у) в том и только в том случае, когда точка М лежит на данной гиперболе (фактически, мы здесь имеем два уравнения— одно для правой, другое для левой ветви гиперболы). Дальнейшие выкладки имеют целью получить уравнение гиперболы в более простом виде. Уединим первый радикал, после чего возведем обе части равенства в квадрат;получим: Или Возводя в квадрат обе части этого равенства, найдем:
Откуда
20.Гипербола. Исследование формы гиперболы. Уравнение, определяющее гиперболу в некоторой системе декартовых прямоугольных координат, есть уравнение второй степени; таким образом, гипербола есть линия второго порядка. Займемся исследованием гиперболы, определенной уравнением Так как каноническое уравнение содержит члены только с четными степенями каждой из текущих координат х, у, то определяемая им гипербола симметрична относительно каждой из координатных осей (доказывается так же, как аналогичное утверждение для эллипса); отсюда ясно, что достаточно рассмотреть лишь часть гиперболы, лежащую в первой координатной четверти. Так как указанная часть гиперболы лежит в верхней полуплоскости, то в полученном уравнении ей соответствует знак +; а так как она вместе с тем лежит в правой полуплоскости, то для всех ее точек х ≥ 0. Таким образом, мы должны исследовать функцию y при условии х ≥ 0 и изобразить ее график. Мы получаем мнимое число. При возрастании х величина у остается мнимой до тех пор, пока х не станет равным а. Полагая в правой части х =a, найдем _ у = 0. Следовательно, точка А(а; 0) является самой левой точкой графика. При дальнейшем возрастании х величина у будет вещественной и положительной уже все время; это сразу видно, так как при х > а имеем у является возрастающей функцией от х (если х ≥ а), т. е. каждый раз, когда увеличивается х, увеличивается также и у. Наконец при бесконечном возрастании х происходит бесконечное же возрастание у (при х → +∞ также и у → +∞).Сопоставляя все, что было сейчас сказано, приходим к следующему заключению: при возрастании х, начиная от х = а, переменная точка М (х; у), описывающая график, движется все время «вправо» и «вверх», имея своимначальным положением точку А(а; 0); удаление точки М как от оси Оу «вправо», так и от оси Ох «вверх» является бесконечным (см.рис.).Присмотримся более внимательно к тому, как именно точка М «уходит в бесконечность». С этой целью мы наряду с уравнением у = заключаем, что при х → +∞ правая часть равенства стремится к нулю; значит, стремится к нулю и MN= Y—y. Обозначим через Р основание перпендикуляра, опущенного из точки М на прямую Пусть Г—какая-нибудь линия, М—переменная точка на ней, l - некоторая прямая. Если возможно такое движение точки М по линии Г, что 1) точка М уходит в бесконечность, 2) при этом расстояние от точки М до прямой l стремится к нулю, — то говорят, что линия Г асимптотически приближается к прямой l. Прямая l в таком случае называется асимптотой линии Г. Употребляя только что указанную терминологию, мы можем следующим образом сформулировать результат исследования: график функции при х → +∞; или прямая есть асимптота графика функции(и в то же время асимптота нашей гиперболы). После того как исследована часть гиперболы, лежащая в первой координатной четверти, общий вид целой гиперболы может быть легко установлен при помощи зеркальных отражений относительно координатных осей.Гипербола, определяемая уравнением Оси симметрии гиперболы называют обычно просто ее осями, точку пересечения осей — центром гиперболы.
определяет гиперболу с полуосями а и b. Рассмотрим теперь уравнение вида: Отсюда ясно, что данное уравнение определяет гиперболу, расположенную так, как показано на рисунке (вершины ее В и В' лежат на оси Оу). Это уравнение также называется каноническим уравнением гиперболы. Две гиперболы, которые определяются уравнениями
21.Эксцентриситет гиперболы. Рациональное выражение фокальных радиусов гиперболы . Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к расстоянию между ее вершинами; обозначив эксцентриситет буквой е, получим: Следовательно, эксцентриситет определяется отношением b \ a, а отношение b \ a в свою очередь определяется эксцентриситетом. Таким образом, эксцентриситет гиперболы характеризует форму ее основного прямоугольника, а значит, и форму самой гиперболы. Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше
22.Директрисы эллипса и гиперболы. Рассмотрим какой-нибудь эллипс и введем декартову прямоугольную систему координат так, чтобы этот эллипс определялся каноническим уравнением Предположим, что рассматриваемый эллипс не является окружностью, т. е. что a ≠b и, следовательно, е ≠ 0. Предположим еще, что этот эллипс вытянут в направлении оси Ох, т. е. что а > b. Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии от него, называются директрисами эллипса. Уравнения директрис в выбранной системе координат имеют вид
23.Парабола. Вывод канонического уравнения параболы. Исследование формы параболы. Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус). Фокус параболы принято обозначать буквой F, расстояние от фокуса до директрисы — буквой р. Величину р называют параметром параболы. Изображение параболы дано на рисунке. Замечание. В соответствии с изложенным ранее говорят, что парабола имеет эксцентриситет е = 1. Чтобы получить искомое уравнение, нужно в данном равенстве заменить переменные r и d их выражениями через текущие координаты х, у. Заметим, что фокус F имеет координаты (p \2;0); приняв это во внимание находим: Обозначим через Q основание перпендикуляра, опущенного из точки М на директрису. Очевидно, точка Q имеет координаты (p \2; y); отсюда получаем: Чтобы получить уравнение параболы в более простом виде, возведем обе части полученного равенства в квадрат и преобразовав получим: При отрицательных значениях х данное уравнение дает мнимые значения у. Следовательно, левее оси Оу ни одной точки параболы нет. При х = 0 получаем у = 0. Таким образом, начало координат лежит на параболе и является самой «левой» ее точкой. Пусть теперь х возрастает, начиная от нуля; как видно из уравнения, при этом у будет все время возрастать. Из уравнения видно также, что если х → +∞, то и у → +∞. Таким образом, переменная точка М (х; у), описывающая рассматриваемую часть параболы, исходит из начала координат и движется «вправо» и «вверх»; удаление точки М как от оси Оу «вправо», так и от оси Ох «вверх» является бесконечным Замечание. Существенны еще два свойства параболы: 1) направление ее в точке О(0; 0) перпендикулярно к оси Ох, 2) часть параболы, лежащая в верхней полуплоскости, своей выпуклостью обращена «вверх». Рисунок выполнен с учетом этих свойств. Мы не будем, однако, доказывать, что они действительно имеют место, так как такого рода исследование линий наиболее естественно проводить средствами математического анализа. После того, как мы установили форму части параболы, лежащей в верхней полуплоскости, установление формы целой параболы уже не требует ни малейшего труда. Для этого достаточно произвести зеркальное отражение относительно оси Ох. Общее представление о целой параболе, заданной уравнением (p > 0) определяет параболу с вершиной в начале координат, расположенную симметрично относительно оси Оу (эти уравнения параболы, как и предыдущие уравнения, называют каноническими.
24.. Пересечение кривой второго порядка с прямой. Берем кривую второго порядка, заданную уравнением Введем еще следующие обозначения: Решая уравнение (*) совместно с уравнением данной прямой
25.Различные виды уравнения плоскости. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0, где А, В, С – координаты вектора -вектор нормали к плоскости.Возможны следующие частные случаи: А = 0 – плоскость параллельна оси Ох В = 0 – плоскость параллельна оси Оу С = 0 – плоскость параллельна оси Оz D = 0 – плоскость проходит через начало координат А = В = 0 – плоскость параллельна плоскости хОу А = С = 0 – плоскость параллельна плоскости хОz В = С = 0 – плоскость параллельна плоскости yOz А = D = 0 – плоскость проходит через ось Ох В = D = 0 – плоскость проходит через ось Оу С = D = 0 – плоскость проходит через ось Oz А = В = D = 0 – плоскость совпадает с плоскостью хОу А = С = D = 0 – плоскость совпадает с плоскостью xOz В = С = D = 0 – плоскость совпадает с плоскостью yOz Уравнение плоскости, проходящей через три точки.Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 860; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.35.27 (0.015 с.) |



 Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше 1−
Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше 1−  ,тем меньше, следовательно, отношение b/a; значит, чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности b = а и е = 0. Итак,для выражений фокальных радиусов имеют место формулы: r1 =√ a – εx, r2 = √a + εx.
,тем меньше, следовательно, отношение b/a; значит, чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности b = а и е = 0. Итак,для выражений фокальных радиусов имеют место формулы: r1 =√ a – εx, r2 = √a + εx.









 .Здесь мы введем в рассмотрение новую величину
.Здесь мы введем в рассмотрение новую величину  геометрический смысл величины b будет раскрыт несколько позднее; сейчас мы только заметим, что с > а, следовательно
геометрический смысл величины b будет раскрыт несколько позднее; сейчас мы только заметим, что с > а, следовательно  ,и величина b —вещественна), вследствие чего последнему уравнению можно придать вид
,и величина b —вещественна), вследствие чего последнему уравнению можно придать вид  .Данное уравнение называется каноническим уравнением гиперболы. Легко доказать, что данное уравнение определяет гиперболу в выбранной нами системе координат.
.Данное уравнение называется каноническим уравнением гиперболы. Легко доказать, что данное уравнение определяет гиперболу в выбранной нами системе координат. .Или
.Или 
 ;
;
 которое при х > а определяет изучаемую сейчас часть гиперболы, рассмотрим еще уравнение
которое при х > а определяет изучаемую сейчас часть гиперболы, рассмотрим еще уравнение  оно определяет прямую с угловым коэффициентом
оно определяет прямую с угловым коэффициентом  , проходящую через начало координат. Часть этой прямой, расположенная в первой координатной четверти, изображена на рисунке (для построения ее использован прямоугольный треугольник ОАВ с катетами ОА = а и АВ = b; очевидно, прямая ОВ как раз и имеет угловой коэффициент
, проходящую через начало координат. Часть этой прямой, расположенная в первой координатной четверти, изображена на рисунке (для построения ее использован прямоугольный треугольник ОАВ с катетами ОА = а и АВ = b; очевидно, прямая ОВ как раз и имеет угловой коэффициент  . Возьмем произвольное значение х (х ≥ а) и рассмотрим две точки: М(х; у) и N(x; Y), где
. Возьмем произвольное значение х (х ≥ а) и рассмотрим две точки: М(х; у) и N(x; Y), где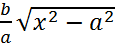 ,
,  .Точка М(х; у) лежит на гиперболе, точка N(x; Y) — на прямой; поскольку обе эти точки имеют одну и ту же абсциссу х, прямая, соединяющая точки М и N, Перпендикулярна к оси Ох (см.рис.). Подсчитаем длину резка MN. Прежде всего, заметим, что
.Точка М(х; у) лежит на гиперболе, точка N(x; Y) — на прямой; поскольку обе эти точки имеют одну и ту же абсциссу х, прямая, соединяющая точки М и N, Перпендикулярна к оси Ох (см.рис.). Подсчитаем длину резка MN. Прежде всего, заметим, что  Отсюда Y >у и, следовательно, MN= Y— у. И
Отсюда Y >у и, следовательно, MN= Y— у. И  . Проанализируем полученное выражение, предполагая, что х → +∞. Знаменатель его представляет собой сумму двух положительных бесконечно растущих слагаемых; следовательно, при х → +∞ знаменатель стремится к (положительной) бесконечности. Числитель этого выражения есть постоянная величина ab. Сопоставляя эти два бстоятельства,
. Проанализируем полученное выражение, предполагая, что х → +∞. Знаменатель его представляет собой сумму двух положительных бесконечно растущих слагаемых; следовательно, при х → +∞ знаменатель стремится к (положительной) бесконечности. Числитель этого выражения есть постоянная величина ab. Сопоставляя эти два бстоятельства, х (МР—расстояние от точки М до этой прямой). Очевидно МР < MN, а так как MN → 0, то, следовательно, и МР → 0. А это мы и хотели доказать. Итак, если переменная точка М уходит в бесконечность по то части гиперболы, которая расположена в первой координатной четверти, то расстояние от тонки М до прямой стремится к нулю.
х (МР—расстояние от точки М до этой прямой). Очевидно МР < MN, а так как MN → 0, то, следовательно, и МР → 0. А это мы и хотели доказать. Итак, если переменная точка М уходит в бесконечность по то части гиперболы, которая расположена в первой координатной четверти, то расстояние от тонки М до прямой стремится к нулю. (т. е. рассматриваемая часть гиперболы) асимптотически приближается к прямой
(т. е. рассматриваемая часть гиперболы) асимптотически приближается к прямой первая из этих прямых нам уже знакома, вторая представляет собой ее зеркальное отражение относительно оси Ох (или оси Оу).
первая из этих прямых нам уже знакома, вторая представляет собой ее зеркальное отражение относительно оси Ох (или оси Оу).
 Очевидно, что основной прямоугольник равносторонней гиперболы есть квадрат; отсюда ясно, что асимптоты равносторонней гиперболы перпендикулярны друг к другу.
Очевидно, что основной прямоугольник равносторонней гиперболы есть квадрат; отсюда ясно, что асимптоты равносторонней гиперболы перпендикулярны друг к другу. , находим:
, находим: 

 , тем меньше, следовательно, отношение b \ a значит, чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник (в направлении оси, соединяющей вершины). В случае равносторонней гиперболы а = b и.
, тем меньше, следовательно, отношение b \ a значит, чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник (в направлении оси, соединяющей вершины). В случае равносторонней гиперболы а = b и. 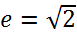 .Рассмотрим произвольную точку М(х;у), лежащую на данной гиперболе. Если r 1 и r 2 — фокальные радиусы этой точки, то
.Рассмотрим произвольную точку М(х;у), лежащую на данной гиперболе. Если r 1 и r 2 — фокальные радиусы этой точки, то 
 для точек левой ветви
для точек левой ветви  )
) 

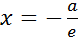
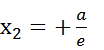 Первую из них мы условимся называть левой, вторую — правой. Так как для эллипса е < 1, то
Первую из них мы условимся называть левой, вторую — правой. Так как для эллипса е < 1, то  . Отсюда следует, что правая директриса расположена правее правой вершины эллипса; аналогично, левая директриса расположена левее его левой вершины. Эллипс вместе с директрисами изображен на рисунке.Рассмотрим какую-нибудь гиперболу и введем декартову прямоугольную систему координат так, чтобы эта гипербола определялась каноническим уравнением
. Отсюда следует, что правая директриса расположена правее правой вершины эллипса; аналогично, левая директриса расположена левее его левой вершины. Эллипс вместе с директрисами изображен на рисунке.Рассмотрим какую-нибудь гиперболу и введем декартову прямоугольную систему координат так, чтобы эта гипербола определялась каноническим уравнением  Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и расположенные симметрично относительно центра на расстоянии от него, называются директрисами гиперболы. Уравнения директрис в выбранной системе координат имеют вид
Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и расположенные симметрично относительно центра на расстоянии от него, называются директрисами гиперболы. Уравнения директрис в выбранной системе координат имеют вид  Первую из них мы условимся называть левой, вторую— правой. Так как для гиперболы е > 1, то
Первую из них мы условимся называть левой, вторую— правой. Так как для гиперболы е > 1, то  . Отсюда следует, что правая директриса расположена между центром и правой вершиной гиперболы; аналогично, левая директриса расположена между центром и левой вершиной. Гипербола вместе с директрисами изображена на следующем рис
. Отсюда следует, что правая директриса расположена между центром и правой вершиной гиперболы; аналогично, левая директриса расположена между центром и левой вершиной. Гипербола вместе с директрисами изображена на следующем рис  есть постоянная величина, равная эксцентриситету эллипса:
есть постоянная величина, равная эксцентриситету эллипса:  Доказательство. Предположим для определенности, что речь идет о правом фокусе и правой директрисе. Пусть, М(х;у) — произвольная точка эллипса (см. рис.). Расстояние от М до правой директрисы выражается равенством
Доказательство. Предположим для определенности, что речь идет о правом фокусе и правой директрисе. Пусть, М(х;у) — произвольная точка эллипса (см. рис.). Расстояние от М до правой директрисы выражается равенством  которое легко усматривается из чертежа; расстояние от точки М до правого фокуса r=ex-a Тогда имеем:
которое легко усматривается из чертежа; расстояние от точки М до правого фокуса r=ex-a Тогда имеем:  Теорема доказана. Теорема. Если r —расстояние от произвольной точки гиперболы до какого-нибудь фокуса, d —расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение
Теорема доказана. Теорема. Если r —расстояние от произвольной точки гиперболы до какого-нибудь фокуса, d —расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение  . Расстояние от точки М до правого фокуса
. Расстояние от точки М до правого фокуса  Из этих соотношений имеем:
Из этих соотношений имеем:  2) Точка М находится на левой половине гиперболы. Тогда расстояние от М до правой директрисы выражается равенством
2) Точка М находится на левой половине гиперболы. Тогда расстояние от М до правой директрисы выражается равенством 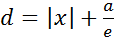 (| x |—расстояние от точки М до оси Оу, расстояние от директрисы до оси Оу, d есть сумма этих расстояний); но так как М находится на левой половине гиперболы, то х есть величина отрицательная, следовательно, | x | = — х, и мы получаем:
(| x |—расстояние от точки М до оси Оу, расстояние от директрисы до оси Оу, d есть сумма этих расстояний); но так как М находится на левой половине гиперболы, то х есть величина отрицательная, следовательно, | x | = — х, и мы получаем:  Расстояние от М до правого фокуса –(ех-а) Тогда имеем:
Расстояние от М до правого фокуса –(ех-а) Тогда имеем:  Теорема доказана.
Теорема доказана.
 (при извлечении корня мы взяли
(при извлечении корня мы взяли  co своим знаком, так как
co своим знаком, так как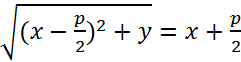 Это и есть уравнение рассматриваемой параболы в назначенной системе координат, так как ему удовлетворяют координаты точки М (х; у) в том и только в том случае,когда точка М лежит на данной параболе.
Это и есть уравнение рассматриваемой параболы в назначенной системе координат, так как ему удовлетворяют координаты точки М (х; у) в том и только в том случае,когда точка М лежит на данной параболе. Легко доказать, что данное уравнение определяет параболу в выбранной нами системе координат. Уравнение
Легко доказать, что данное уравнение определяет параболу в выбранной нами системе координат. Уравнение 
 . Мы получаем на параболе две точки, симметричные относительно оси; Таким образом, есть длина хорды параболы, проведенной перпендикулярно к оси на расстоянии в одну единицу длины от вершины. Мы видим, что длина этой хорды тем больше, чем больше р. Следовательно, параметр р характеризует «ширину» области, ограниченной параболой, при условии, что эта «ширина» измеряется перпендикулярно к оси на определенном расстоянии от вершины. Уравнение (при положительном р) сводится к уравнению путем замены х на — x, т. е. путем преобразования координат, которое соответствует изменению направления оси Ох на противоположное. Отсюда следует, что уравнение
. Мы получаем на параболе две точки, симметричные относительно оси; Таким образом, есть длина хорды параболы, проведенной перпендикулярно к оси на расстоянии в одну единицу длины от вершины. Мы видим, что длина этой хорды тем больше, чем больше р. Следовательно, параметр р характеризует «ширину» области, ограниченной параболой, при условии, что эта «ширина» измеряется перпендикулярно к оси на определенном расстоянии от вершины. Уравнение (при положительном р) сводится к уравнению путем замены х на — x, т. е. путем преобразования координат, которое соответствует изменению направления оси Ох на противоположное. Отсюда следует, что уравнение 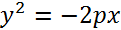 также определяет параболу, ось которой совмещена с осью Ох, а вершина — с началом координат, но которая расположена в левой полуплоскости
также определяет параболу, ось которой совмещена с осью Ох, а вершина — с началом координат, но которая расположена в левой полуплоскости 

 (*),где
(*),где  .
. 
 .
. 
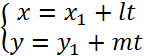 получим уравнение
получим уравнение 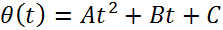 где, как показывает легкий подсчет,
где, как показывает легкий подсчет, 

 Мы теперь предполагаем, что
Мы теперь предполагаем, что  так что полученное уравнение имеет два (различных или совпадающих) корня tl, t2. Пусть tl = t2тогда прямая пересекает кривую (*) в двух совпадающих точках и называется касательной к этой кривой: обе точки пересечения слились в одну точку касания. Для нахождения уравнения касательной удобно взять за точку М0 = (х0, у0) прямой как раз ту точку, которая принадлежит и кривой (*), и прямой. Тогда
так что полученное уравнение имеет два (различных или совпадающих) корня tl, t2. Пусть tl = t2тогда прямая пересекает кривую (*) в двух совпадающих точках и называется касательной к этой кривой: обе точки пересечения слились в одну точку касания. Для нахождения уравнения касательной удобно взять за точку М0 = (х0, у0) прямой как раз ту точку, которая принадлежит и кривой (*), и прямой. Тогда  и уравнение принимает вид t(At + 2B) = 0;оно имеет корень t = 0. Если в точке М0=(х0,у0) сливаются обе точки пересечения кривой (*) и прямой, то оба корня совпадают и равны нулю. А это может случиться лишь при
и уравнение принимает вид t(At + 2B) = 0;оно имеет корень t = 0. Если в точке М0=(х0,у0) сливаются обе точки пересечения кривой (*) и прямой, то оба корня совпадают и равны нулю. А это может случиться лишь при  Откуда
Откуда  Следовательно, уравнение касательной получает вид
Следовательно, уравнение касательной получает вид 

 ,
,  были компланарны.
были компланарны.  Таким образом,
Таким образом,  ,
,  ,
,  .Уравнение плоскости, проходящей через три точки:
.Уравнение плоскости, проходящей через три точки: 



