
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанное произведение трех векторов. Его выражение через координаты векторов в ортонормированном базисе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
е1,е2,е3 единичные векторы а={α1,α2,α3}, b={β1,β2,β3}, c={µ1,µ2,µ3} (a,b,c)=(α1*e1+ α2*e2+ α3*e3+ β1*e1+ β2*e2+ β3*e3+ µ1*e1+ µ2*e2+ µ3*e3)= Смешанное произведение
Смешанное произведение
11.Деление отрезка в данном отношении. Пусть на плоскости даны две произвольные различные точки, из которых одна считается первой, другая – второй. Обозначим их в заданном порядке через М1 и М2. Проведем через данные точки прямую j и назначим на ней положительное направление, тем самым мы сделаем ее осью. Пусть, далее, М – еще одна точка оси j, расположенная на ней как угодно и исключением только одного случая: она не должна совпадать с точкой М2. Число µ=М1М/ММ2, где М1М и ММ2 суть величины направленных отрезков М1М и ММ2 оси j, называется отношением, в котором точка М делит направленный отрезок М1М2. Замечание 2. Число µ не зависит и от выбора масштаба для измерения длин. В самом деле, при изменении масштаба величины отрезков на оси М1М2 умножатся на одно и то же число и следовательно отношение М1М/ММ2 не изменится. Замечание 3. Если не исключать возможности совпадения точки М с точкой М2, то в том случае, когда М совпадет с М2, равенство не определяет никакого числа.
12. Различные виды уравнения прямой на плоскости. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и вектору нормали Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0. Уравнение прямой, проходящей через две точки Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:
если х 1 ≠ х2 и х = х 1, если х 1 = х2. Дробь Уравнение прямой по точке и угловому коэффициенту Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить Уравнение прямой по точке и направляющему вектору По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой. Определение. Каждый ненулевой вектор Ах + Ву + С = 0.
13. Нормальное уравнение прямой на плоскости. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Если обе части уравнения Ах + Ву + С = 0 разделить на число
xcosφ + ysinφ - p = 0 – нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
14. Угол межу двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых. Определение. Если заданы две прямые y = k1 x + b1, y = k 2x + b2, то острый угол между этими прямыми будет определяться как
Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1 = -1/ k2. Теорема. Прямые Ах + Ву + С = 0 и А 1 х + В1 у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = λА, В1 = λВ. Если еще и С1 = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых. Если уравнения прямой заданы в общем виде A 1 x + B 1 y + C 1 = 0, A 2 x + B 2 y + C 2 = 0, (6) угол между ними определяется по формуле
Условия параллельности двух прямых: а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k 1 = k 2. (8) б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
15. Расстояние от точки до прямой на плоскости. Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как Доказательство. Пусть точка М 1(х 1, у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1: Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x 0) + B(y – y0) + Ax0 + By0 + C = 0, то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
Теорема доказана.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.115.120 (0.009 с.) |


 в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов
в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов  и
и  :
:
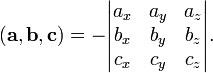
 Замечание1.Число µ не зависит от того, как выбрано положительное направление на прямой j, определяемой точками М1 и М2.
Замечание1.Число µ не зависит от того, как выбрано положительное направление на прямой j, определяемой точками М1 и М2.

 = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.
 , то полученное уравнение называется уравнением прямой с угловым коэффициентомk.
, то полученное уравнение называется уравнением прямой с угловым коэффициентомk. (α1, α2), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой
(α1, α2), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой , которое называется нормирующем множителем, то получим
, которое называется нормирующем множителем, то получим .
.


 (7)
(7)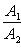


 (9)
(9)


 (10)
(10)
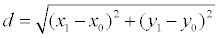 (1)
(1)




