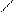Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Усне додавання та віднімання з переходом через розрядСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Логіка подання навчального матеріалу така сама, як і у випадках без переходу через десяток. Спочатку розглядаються часткові випадки додавання та віднімання (1) додавання та віднімання одноцифрового числа з переходом через десяток; 2) додавання та віднімання круглого числа з переходом через десяток) і лише потім – загальний випадок (додавання і віднімання двоцифрових чисел з переходом через розряд). У межах певних випадків обчислення застосовуються різні способи обчислення. Додавання та віднімання одноцифрового числа з переходом через розряд.
круглі десятки та двоцифрове число. Спосіб міркування в обох випадках однаковий: двоцифровий доданок подають у вигляді суми десятків та одиниць, другий доданок додають до одиниць і отриманий результат додають до десятків. Теоретичною підставою розв’язання є правило додавання числа до суми. Але цей випадок відрізняється від попередніх тим, що в результаті додавання одиниць одержали число більше за 10, тому відбувається перехід через десяток. Аналогічно відбувається ознайомлення з відніманням одноцифрового числа з переходом через розряд.
53=40+13. З 13 будемо віднімати 8, отримаємо 5; додамо 5 до першого доданка 40, буде 45. Можна узагальнити спосіб розв’язування розглянутих випадків віднімання, оскільки він базується на правилі віднімання числа від суми, і визначити ООД цього прийому обчислення: Віднімання одноцифрового числа з двоцифрового 1. Подаю двоцифрове зменшуване у вигляді суми зручних доданків (другий доданок: 10 + одиниці зменшуваного). 2. Віднімаю від'ємник з другого доданка. 3. Додаю перший доданок до отриманої різниці. 4. Записую (читаю) відповідь. З метою розвитку варіативності мислення дітей, можна перенести прийом обчислення по частинах на нові випадки додавання та віднімання. Актуалізуємо спосіб обчислення по частинах у випадках додавання та віднімання з переходом через десяток у межах 20 (12–5 та 7+4). Ставимо проблемне запитання: „Чи можна при обчисленні значень виразів: 72–5 та 67+4 міркувати так само?”
Від’ємник (другий доданок) замінюємо сумою зручних доданків; зменшуємо (доповнюємо) двоцифрове число до круглого; віднімаємо (додаємо) від (до) круглого числа решту одиниць. Отже, спосіб міркування однаковий – на підставі правил віднімання суми з числа або додавання суми до числа. Далі можна перенести спосіб округлення на ці випадки додавання і віднімання. Зауважуємо, якщо число закінчується цифрою 5, або 6, або 7, або 8, або 9, то його можна замінити близьким круглим числом. Актуалізуємо спосіб округлення для випадків додавання та віднімання з переходом через десяток в межах 20 та переносимо його в нову ситуацію. Наприклад, чи можна міркувати так само?
Незважаючи на те, що перший доданок тут двоцифрове число, спосіб міркування такий самий, як і в попередньому випадку; його теоретична основа – знання зміни суми в залежності від зміни одного доданка та знання зміни різниці в залежності від зміни від’ємника.
3+3
3+3
3+23 З’ясовуємо, чим відрізняється третій випадок обчислення від розглянутих двох (на відміну від двох попередніх, в ньому другий доданок двоцифрове число; він складається із 2 десятків та 6 одиниць). Визначаємо вплив цієї зміни на розв’язання: число 26 замінимо сумою зручних доданків, один з яких число 3, тому що воно доповнює 37 до найближчого круглого числа, а другий доданок – двоцифрове число 23. Так само, як і у попередніх випадках, ми доповнюємо перший доданок до круглого числа, а далі до нього додаємо інший доданок. Існує можливість узагальнити спосіб додавання по частинах для всіх розглянутих випадків.
2+3
2+3
22+3
подамо у вигляді суми зручних доданків: 25 = 22 + 3. І так само, як і в перших двох розв’язаннях, спочатку зменшуване зменшимо до круглого числа, а потім від круглого числа віднімемо решту одиниць. Спосіб обчислення той самий, заснований на правилі віднімання суми з числа, тому є сенс його узагальнити для розглянутих випадків. Додавання і віднімання по частинах можна здійснити за допомогою подання другого доданка або від’ємника сумою зручних доданків або розрядних доданків.
24+5 7+41
20+9 40+8
1) Подаю 2) 3) Треба зазначити, що при додаванні по частинах ми другий доданок замінюємо сумою і подальші міркування здійснюються за правилом додавання суми до числа. Однак можна замінити сумою й перший доданок. Тоді подальші міркування здійснюються за правилом додавання числа до суми. Таким чином, переносимо відомий дітям спосіб міркування на підставі правила додавання числа до суми (для випадку 36 – 7) у нову ситуацію. 36+27=30+6+27=57+6=63 36+27=33+3+27=33+30=63
30+6 33+ 3 Аналогічно можна розглянути віднімання з переходом через десяток на підставі правила віднімання числа із суми. 84–29=80+4–29=51+4 = 55 84 - 29=5+79-29=5+50=55
80+4 5 + 79
1) Подаю 2) 3) Додаю до одержаного результату інший доданок. Порозрядне додавання і віднімання двоцифрових чисел з переходом через розряд. Ознайомлення можна здійснити за допомогою співставлення випадку додавання двоцифрових чисел без переходу через десяток та з переходом через нього.
виконавши дію додавання з десятками та окремо з одиницями, додають одержані результати. Учитель формулює проблемне запитання: „Чи можна при обчисленні значення другого виразу міркувати так само?”. Існує можливість узагальнити спосіб порозрядного додавання для випадків додавання двоцифрових чисел як без переходу, так і з переходом через розряд. Прийом порозрядного додавання 1. Подаю перший доданок у вигляді суми десятків і одиниць. 2. Подаю другий доданок у вигляді суми десятків та одиниць. 3. Додаю десятки. 4. Додаю одиниці. 5. Додаю отримані суми. 6. Читаю (записую) відповідь.
Наприклад: 48 + 29 = 40 + 8 + 20 + 9 = 60 + 17 = 77
40+8 20+9
40+6 20+2 Ознайомлення з випадком порозрядного віднімання можна здійснити так само, на підставі порівняння випадків порозрядного віднімання без переходу та з переходом через розряд. Учні дістають висновку, що коли з одиниць зменшуваного не можна відняти одиниці від'ємника, то зменшуване подають у вигляді суми зручних доданків, а далі міркують так само, як і у випадках віднімання без переходу через розряд. Прийом порозрядного віднімання 1. Перевіряю чи можна з одиниць зменшуваного відняти одиниці від’ємника. Так Ні 2. Подаю зменшуване у вигляді суми розрядних доданків зручних доданків 3. Подаю від'ємник у вигляді суми десятків та одиниць. 4. Віднімаю десятки. 5. Віднімаю одиниці. 6. Додаю отримані різниці. 7. Читаю (записую) результат.
50+14 30+7
60+4 30+3 Корисним буде перенесення прийому округлення на випадки додавання та віднімання, що розглядаються. Співствляючи міркування способом округлення при додаванні та відніманні одноцифрового числа з міркуванням при додаванні й відніманні двоцифрових чисел, з’ясовуємо, що вони схожі.
Спосіб округлення Якщо один з доданків (від'ємник) закінчується цифрою 6, 7, 8, 9, то 1. Замінюю один з доданків (від'ємник) близьким круглим числом. 2. Додаватиму (відніматиму) кругле число. Дивлюся, на скільки більше додали (відняли)? 3. Віднімаю (додаю) стільки ж одиниць. 4. Записую відповідь. Учні вчаться знаходити значення сум та різниць різними способами і згодом обирають найбільш привабливий.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 Прийом на підставі правила додавання числа до суми та правила віднімання числа із суми. Ознайомлення здійснюється на підставі перенесення відомого способу міркування в нову ситуацію.
Прийом на підставі правила додавання числа до суми та правила віднімання числа із суми. Ознайомлення здійснюється на підставі перенесення відомого способу міркування в нову ситуацію.
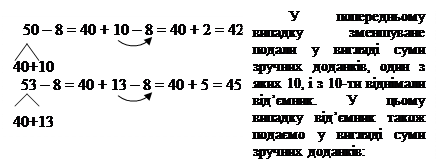




 72 - 5 = 72 - - =70 - =
72 - 5 = 72 - - =70 - =


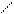

 67 + 4= 67 + + =80+ =
67 + 4= 67 + + =80+ =
 8
8
 Додавання та віднімання двоцифрових чисел. Спосіб обчислення по частинах. Цей спосіб було введено ще в межах 10-ти, перенесено на випадки обчислення в межах 20-ти та застосовано при додаванні (відніманні) одноцифрового числа до (із) двоцифрового. Тому можна вважати, що він найкраще засвоєний учнями, ніж решта способів. Виходячи з цього, саме цей спосіб будемо розглядати першим.
Додавання та віднімання двоцифрових чисел. Спосіб обчислення по частинах. Цей спосіб було введено ще в межах 10-ти, перенесено на випадки обчислення в межах 20-ти та застосовано при додаванні (відніманні) одноцифрового числа до (із) двоцифрового. Тому можна вважати, що він найкраще засвоєний учнями, ніж решта способів. Виходячи з цього, саме цей спосіб будемо розглядати першим. 7 + 6 = 7 + 3 + 3 = 10 + 3 = 13.
7 + 6 = 7 + 3 + 3 = 10 + 3 = 13.

 Аналогічно ознайомлюємо учнів із способом віднімання по частинах.
Аналогічно ознайомлюємо учнів із способом віднімання по частинах.

 12 - 5 = 12 - 2 - 3 = 10 - 3 = 7
12 - 5 = 12 - 2 - 3 = 10 - 3 = 7

 42 - 5 = 42 - 2 - 3 = 40 - 3 = 37
42 - 5 = 42 - 2 - 3 = 40 - 3 = 37 42 - 25 = 42 - 22 - 3 = 20 - 3 = 17
42 - 25 = 42 - 22 - 3 = 20 - 3 = 17


 по частинах (на підставі правила додавання суми до числа або правила віднімання суми від числа)
по частинах (на підставі правила додавання суми до числа або правила віднімання суми від числа)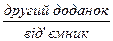 сумою розрядних або зручних доданків.
сумою розрядних або зручних доданків.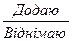 один доданок.
один доданок. одержаного результату інший доданок.
одержаного результату інший доданок.



 сумою розрядних або зручних доданків.
сумою розрядних або зручних доданків. одного доданка число.
одного доданка число.