Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Методика навчання табличного додавання та віднімання чисел в межах 10Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наочні посібники та дидактичний матеріал Демонстраційні: дошка, що розлінована в клітинку; набірне полотно для роботи з предметними картинками, картками з цифрами; яскраві сюжетні картинки з прорізами, в які вставляються окремі зображення предметів, (наприклад, галявина – на ній прорізи для грибів, дерева – на них прорізи для пташок, білочок, тарілки – на них прорізи для яблук, груш, апельсинів тощо; набори предметних картинок, геометричних фігур різного розміру і кольору; набори об’ємних фігур (кубики тощо).). Індивідуальні: набірне полотно; набори геометричних фігур різного кольору і розміру; картки з цифрами і знаками. Ознайомлення учнів з конкретним змістом арифметичних дій додавання і віднімання відбувається під час оперування множинами предметів. Об’єднуючи елементи двох множин, що не перетинаються, знаходимо численність поєднаної множини. Операція об’єднання двох множин, що не перетинаються, розкриває конкретний зміст дії додавання. Операція утворення доповнення до підмножини формує зміст дії віднімання. Численність множини, що залишилася після вилучення частини її елементів, відповідає остачі. Операція вилучення частини елементів множини розкриває конкретний зміст дії віднімання. Під час пояснення змісту арифметичних дій в початковій школі доцільно використовувати принцип співвіднесення предметної, вербальної, схематичної і символічної моделей і перехід від однієї моделі до іншої. Такий підхід особливо важливий з точки зору подальшого навчання учнів розв’язування задач. Розглянемо різні методичні підходи до опрацювання теми. Підготовка до опрацювання дій додавання та віднімання розпочинається з перших уроків математики як за методичною системою М.В. Богдановича, так і за методичною системою Л.П. Кочиної та зводиться до знаходження суми або різниці двох предметних множин перелічуванням, що неможливо зробити без предметів чи малюнків. За методичною системою Л.П. Кочиної робота щодо вивчення дій додавання та віднімання будується в такій послідовності. На першому етапі (підготовчий період) діти знаходять суму або різницю двох предметних множин перелічуванням на основі практичних вправ. Підготовчий період триває до закінчення вивчення нумерації чисел першої п'ятірки. На другому етапі відбувається безпосереднє ознайомлення з діями додавання та віднімання (одночасно), діти усвідомлюють зміст дій додавання та віднімання та взаємозв'язок між ними. Ознайомлення з назвами компонентів і результатами дій додавання та віднімання також відбувається одночасно. На третьому етапі учні вчаться знаходити значення виразів в межах кожного числа на основі складу числа. Наступний етап — четвертий — присвячується складанню та засвоєнню таблиць додавання та віднімання. На п’ятому етапі формується вміння знаходити значення виразів з кількома доданками або кількома від'ємниками. На останньому етапі діти вчаться користуватися узагальненою таблицею Піфагора. У вивченні дій додавання та віднімання в межах 10 за методичною системою М.В Богдановича обрано дещо іншу послідовність. Тут можна виділити такі етапи. 1. Знаходження суми або різниці двох предметних множин перелічуванням предметів (ці операції виконуються на підготовчому етапі при вивченні нумерації чисел). 2. Ознайомлення спочатку з дією додавання, а потім віднімання; зв’язок між ними та символікою цих дій (така робота також здійснюється під час вивчення нумерації). 3. Ознайомлення з назвами компонентів і результатом дії додавання (безпосереднє ознайомлення з назвами компонентів і результатом дії віднімання відбувається значно пізніше). 4. Складання і заучування таблиць додавання та віднімання в межах 10; застосування табличних результатів для обчислення виразів на дві дії (однакових чи різних). 5. Ознайомлення з прийомами додавання та віднімання числа частинами (групами), а також переставною властивістю дії віднімання. Якщо порівнювати різні методичні підходи цих учених, то до основних відмінностей слід віднести: - Процес первинного ознайомлення з діями додавання та віднімання. За методичною системою Л.П. Кочиної ознайомлення з діями додавання та віднімання відбувається одночасно після вивчення нумерації чисел першої п'ятірки, а за методичною системою М.В. Богдановича ознайомлення з діями додавання та віднімання розмежовується в часі (після вивчення числа і цифри 5 діти ознайомлюються з дією додавання, а після вивчення числа і цифри 7 з дією віднімання), що пояснюється складністю засвоєння математичної термінології, для якої потрібен додатковий час; - Послідовність ознайомлення учнів з назвами компонентів і результатами дій додавання та віднімання. На думку Л.П. Кочиної ці питання доцільно розглядати одночасно після вивчення нумерації чисел у межах 10, на початку теми „Додавання та віднімання в межах 10”. За методичною системою М.В. Богдановича ознайомлення учнів з назвами компонентів і результатом дії додавання відбувається на початку вивчення теми „Додавання та віднімання в межах 10”, а з назвами компонентів і результатом дії віднімання наприкінці першого класу; - Особливості ознайомлення учнів з додаванням та відніманням у межах 10. За методичною системою Л.П. Кочиної опрацювання теми „Додавання та віднімання в межах 10” розпочинається з одночасного вивчення складу числа та додавання і віднімання в межах цього числа. Доцільність такого підходу обґрунтовується тим, що поняття „склад числа” і „додавання чисел” мають спільну теоретичну основу — об'єднання двох множин, а далі на основі взаємозв’язку дій додавання та віднімання: з прикладу на додавання можна скласти два приклади на віднімання. І тільки наступний етап присвячується складанню та засвоєнню таблиць додавання та віднімання. М.В. Богданович пропонує вивчення теми „Додавання та віднімання в межах 10” розпочинати зі складання і заучування таблиць додавання та віднімання в межах 10, оскільки ознайомлення зі складом числа та з додаванням і відніманням в межах кожного числа доцільно опрацьовувати паралельно ще під час ознайомлення з нумерацією в межах 10. Крім того, по-різному вводяться прийоми обчислень. За методичною системою М.В. Богдановича основний прийом обчислення під час вивчення кожної таблиці додавання і віднімання в межах 10 – це склад числа та взаємозв’язок дій додавання і віднімання. З іншими прийомами обчислень (додавання і віднімання числа частинами (групами) та переставною властивістю дії додавання учні ознайомлюються значно пізніше). Л.П. Кочина вважає, що з прийомами обчислень учнів доцільно ознайомлювати раніше: додавання та віднімання по 1-му (після таблиці додавання і віднімання 1); додавання і віднімання числа частинами (після таблиці додавання та віднімання 2-х); а також передбачено ознайомлення з переставною властивістю додавання (після таблиці додавання та віднімання 5-ти). Розкриємо докладніше ще один з методичних підходів, під час опрацювання дій додавання та віднімання в межах 10, який відповідає вимогам Державного стандарту початкової загальної освіти та нової навчальної програми для учнів початкової школи. На етапі вивчення нумерації чисел в межах 10, ще до введення дій додавання і віднімання діти виконують завдання по оперуванню предметними множинами, тобто відбувається підготовча робота. Підготовча робота до ознайомлення з діями додавання та віднімання здійснюється за допомогою практичних вправ, під час яких діти викладають на парті геометричні фігури та об’єднуючи їх, показують усі фігури. Таким чином, спочатку формується поняття про об’єднання елементів двох множин, що не перетинаються. Діти дістають висновку, щоб показати всі предмети, треба їх об’єднати – це означає присунути, змішати тощо. Аналогічно діти вправляються у виключенні частини множини та показу остачі. Щоб показати остачу, решту, треба виключати – це означає відсунути, забрати, відрізати тощо. Перелічуючи кількість елементів об’єднаної множини діти впевнюються в тому, що коли об’єднуємо стає більше; щоб стало більше, треба об’єднати. Коли виключаємо стає менше, щоб стало менше, треба виключати. Наступним кроком є схематичне зображення операцій об’єднання чи виключення. Спочатку діти виконують аналогічні завдання практично, а потім виконують рисунок. Об’єднуючи – обводять замкненою кривою лінією усі фігури, виключаючи – закреслюють кілька фігур та обводять замкненою кривою остачу. Після того, як діти навчилися зображати об’єднання або виключення схематично за допомогою геометричних фігур, переходимо до навчання схематичного зображення за допомогою відрізків. На наступному етапі здійснюється ознайомлення з конкретним змістом арифметичних дій додавання та віднімання: вчимо дітей пов’язувати практичну дію об’єднання елементів двох множин з арифметичною дією додавання, а практичну дію щодо виключення частини елементів множини з арифметичною дією віднімання. Таким чином формується поняття про те, що коли додаємо стає більше, а коли віднімаємо залишається менше. На цьому етапі також відбувається ознаймлення учнів із знаками додавання та віднімання; навчання їх запису; вводяться поняття „вираз”, „значення виразу”. З цією метою доцільно пропонувати вправи типу: 1. Покладіть на парту зліва 5 червоних квадратів. Покладіть справа 2 жовті квадрати. Присуньте жовті квадрати до червоних. Покажіть всі квадрати. Що ми зробили з квадратами? Ми присунули - об'єднали! Всього квадратів 5 і ще 2. Коли квадрати об'єднали, їх стало більше. Об’єднати – це означає додати. Додавання - це арифметична дія, яка виконується між числами. Таким чином, 5 і ще 2 - це значить до 5 додати 2, одержимо 7. Це можна записати так: 5+2 = 7 Коли об'єднуємо стає більше. Об’єднати – це означає додати. Тому, коли додаємо стає більше. Щоб стало більше треба об'єднати - додати! 2. Поклади на парту 8 кружків. 3 круги відсунь. Покажи круги, що залишилися. Що ми зробили? Ми відсунули - виключили! Залишилося кругів 8 без 3. Коли круги виключили, їх стало менше, ніж було! Виключити – це означає відняти. Віднімання - це арифметична дія, яка виконується між числами. Таким чином, 8 без 3 - це значить із 8 відняти 3, одержимо 5. Це можна записати так: 8 – 3 = 5. Коли виключаємо стає менше. Виключити – це означає відняти. Тому, коли віднімаємо стає менше. Щоб стало менше – треба відняти! Учні розглядають зроблені записи: 5 + 2 = 7 та 8 – 3 = 5, і з’ясовують, що в них спільною є наявність знаку рівності, то їх можна назвати одним словом „рівність”. Ліворуч від знака рівності записані числа, що поєднані знаком плюс або мінус: 5 + 2 та 8 - 3 – це вирази. Праворуч від знака рівності записані числа 7 або 5 – це значення виразів. З метою первинного закріпленні конкретного змісту арифметичних дій додавання і віднімання учні до малюнків, на яких проілюстровано об’єднання або вилучення складають вирази чи рівності; перевіряють чи правильно складено до малюнку вираз або рівність, виправляють помилки, якщо вони є. Наприклад:
? 5?
Практичні вправи на об’єднання або виключення доповнюються завданням на складання виразу з карток з числами й знаками арифметичних дій та знаходження значення виразу тощо. Далі діти вибирають вираз до схематичного рисунку або, навпаки, схематичний рисунок до виразу:
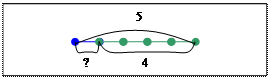
Також учні складають по дві рівності на додавання і дві на віднімання за рисунками, на яких множину геометричних фігур розбито на дві підмножини за спільною ознакою (кольором; розміром; формою), або за картками „доміно”, або за схемами, що складаються з двох відрізків. Аналогічним чином, на підставі конкретного змісту арифметичних дій додавання і віднімання, складаємо по дві рівності на додавання та дві – на віднімання на підставі складу числа. На цьому етапі навчання виконуємо додавання та віднімання за числовим променем:
Додаючи числа крокуємо „вперед” - праворуч, а віднімаючи – „назад” – ліворуч, на стільки кроків, скільки вказує число, що записано у виразі на другому місці.
4 + 3 4 – це перший доданок, 3 – це другий доданок. – Перерахуйте кружечки або додайте 3 червоні кружечки по одному. Запишіть рівність: 4 + 3 = 7. Ми отримали в результаті додавання число 7? Число, яке отримують в результаті дії додавання називають значенням суми. Число 7 – це значення суми.
? Покажіть усі трикутники. Щоб дізнатися, скільки всього трикутників, треба об’єднувати. Тож назвіть схему, на якій відрізок, позначений знаком запитання, є об’єднанням двох відрізків (такою схемою є друга). Жовтий відрізок на схемі означає, що жовтих трикутників 5. Синій відрізок на схемі означає, що синіх – 1. Цілий відрізок, що складається з двох частин, показує усі трикутники – і жовті, і сині. Всього трикутників більше, ніж окремо жовтих; ніж окремо синіх. Більше число знаходимо дією додавання. Складаємо вираз: 5 + 1. Число 5 – перший доданок. Число 1 другий доданок. Знаходимо значення виразу. Число 6 – значення суми. Показуємо на схемі перший доданок, другий доданок, значення суми.
сума.
другий доданок-двома рисками, а значення суми – хвилястою лінією. Математичний вираз “ сума”. Опрацювання зазначеної теми розпочинається з читання рівностей з назвами компонентів. 5 + 1 = 6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 923; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |




 9 6 4
9 6 4













 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 

 Назва компонентів і результату арифметичної дії додавання. Ознайомлюючи учнів з назвами компонентів і результатом арифметичної дії додавання,їм пропонується практичне завдання: покласти на парту 4 зелені та 3 червоні кружечки, об’єднати ці кружечки, скласти та прочитати вираз.
Назва компонентів і результату арифметичної дії додавання. Ознайомлюючи учнів з назвами компонентів і результатом арифметичної дії додавання,їм пропонується практичне завдання: покласти на парту 4 зелені та 3 червоні кружечки, об’єднати ці кружечки, скласти та прочитати вираз.



 Далі переходимо до схематичного зображення доданків та суми. Наприклад:
Далі переходимо до схематичного зображення доданків та суми. Наприклад: –
–  Виберіть схему до малюнка: 1)
Виберіть схему до малюнка: 1)








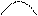
 ?
?


 2)
2)


 1 доданок 2 доданок
1 доданок 2 доданок