
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Й доданок 2-й доданок значення сумиСодержание книги
Поиск на нашем сайте
Після чого вчитель повідомляє, що вираз, який записано ліворуч від знака „=”, називається так само, як і результат – „сума”! Якщо між числами стоїть знак „+”, то записана сума. Щоб записати суму, треба між числами поставити знак „+”, а, щоб знайти значення суми, треба ці числа додати! Отже, треба розрізняти поняття „сума” як назву виразу та „значення суми” – як числове значення виразу. На етапі первинного закріплення діти підкреслюють або записують математичні вирази „суми” двох даних чисел. Переставний закон додавання. Ознайомлення з переставним законом додавання здійснюємо через співставлення рівностей, що складені за карткою „доміно”, і підводимо дітей до формулювання закону на підставі індуктивних узагальнень. За числовими фігурами складіть рівності на додавання. Прочитайте рівності. Що цікавого ви помітили?
Після виконання завдання учні роблять висновок: у цих рівностях переставили доданки: перший доданок став другим, а другий, навпаки, – першим; значення суми від цієї перестановки не змінилося. Аналогічне завдання можна запропонувати учням з відрізками:
5 3 + 2 =2 + 3
Застосовуємо переставний закон додавання для визначення значень виразів: 1. Порівняйте суми. Чим вони схожі? Чим відрізняються? Що можна сказати про результати сум? Чому? 5 + 2 3 + 4 7 + 1 5 + 6 8 + 7 4 + 9 7 + 3 2 + 5 4 + 3 1 + 7 6 + 3 7 + 8 4 + 6 3 + 7 Коментар: перший доданок 5, другий доданок 2; перший доданок 2, другий доданок 5; ці вирази схожі тим, що в них однакові доданки, а відрізняються порядком запису доданків; доданки переставили, від цього значення суми не змінюється, тому ці вирази мають однакові значення... Не мають однакових значень вирази: у 4-му стовпчику та в 6-му, тому що в них доданки неоднакові. 2. Порівняйте записи в кожному стовпчику. Чи допоможе перша рівність обчислити значення другого виразу? Чому? Знайдіть значення другого виразу в кожному стовпчику. 7 + 2 = 9 4 + 2 = 6 3 + 2 = 5 9 + 1 = 10 4 + 5 = 9 2 + 7 2 + 5 2 + 3 1 + 9 5 + 4
Значення якої суми ми не змогли записати відразу, не рахуючи? Чому?
Й доданок 2-й доданок
Сума Аркушем паперу прикриваємо на схемі по черзі перший, а потім другий „доданок”. Визначаємо, що залишилось. Коли прикрили аркушем один з „доданків”, ми виключили. Учні дістають висновку: якщо від суми двох доданків відняти один доданок, то одержимо інший доданок. Треба зазначити, що частіше в методичній літературі питання про взаємозв’язок дій додавання та віднімання розглядається як складання з однієї рівності на додавання двох рівностей на віднімання. Тепер можна ввести означення дії віднімання. З цією метою діти коментують, як з однієї рівності на додавання склали дві рівності на віднімання: із суми відняли перший доданок і одержали другий доданок; із суми відняли другий доданок і одержали перший доданок. Знаходили один із доданків - із суми віднімали інший доданок.
5 + 3 = 8 8 – 5 = 3
Знаходження невідомого доданка. Ознайомлення з правилом знаходження невідомого доданка можна здійснити, створивши ситуацію, коли відомо значення суми і один доданок, а інший доданок невідомий. Наприклад: у Вані в двох руках 7 паличок. У правій руці 3 палички, а скільки паличок в лівій руці, він нам не показав, і порахувати ми їх не можемо. Як дізнатися, скільки паличок у Вані в лівій руці? ? 3
? + 3 = Учні міркують так: 7 паличок в обох руках, а в правій - тільки 3, отже, до числа 7 входять 3 палички, які Ваня тримає в правій руці; щоб дізнатися, скільки паличок у лівій руці, треба з 7-ми виключити 3. Учні пояснюють за схематичним малюнком, що означають відомі числа та невідоме число, встановлюють, що відоме значення суми і другий доданок, отже треба знайти перший доданок. Згадують, як одержати перший доданок, і дістають висновку: щоб знайти невідомий доданок, треба від значення суми відняти відомий доданок.
Математичний вираз „різниця”. Ознайомлення з поняттям „різниця” можна здійснити, запропонувавши учням розбити вирази на дві групи. 5 + 1 7 – 2 4 + 2 9 – 2 6 + 2 10 – 1 3 + 1 8 + 2 4 + 0 4 – 2 5 + 2 7 – 7 7 + 2 8 – 0 Учні розбивають вирази на групи згідно знаку, який стоїть між числами, тому до першої групи входять суми, а до другої – вирази, в яких між числами стоїть знак мінус. Назву виразів першої групи учні вже знають (якщо між числами записаний знак +, то це математичний вираз сума). У виразах другої групи між числами стоїть знак мінус, і вчитель повідомляє: „Якщо між числами стоїть знак мінус, то записано математичний вираз „різниця”. Щоб записати різницю, треба між числами поставити знак мінус”. Далі учні обчислюють значення сум і різниць. На етапі первинного закріплення поняття „різниця” школярам пропонується обчислити спочатку значення різниць, а потім обчислити значення сум. Назва компонентів дії віднімання. На початку вивчення теми вчитель повідомляє, що так само, як і при додаванні, при відніманні числа мають свої назви. Учні згадують, що при відніманні одержують менше число. Отже, при відніманні число, з якого ми віднімаємо зменшується, тому воно називається зменшуваним. Число, яке віднімають називається за характером дії від’ємник. І результат дії віднімання називається так само, як і вираз, що записано ліворуч від знака рівності, але зі словом „значення” – значення різниці.
різниця від’ємник Далі діти показують на схемі дужкою зменшуване, від’ємник і значення різниці; записують відповідні рівності. Також корисні завдання на складання рівностей під диктовку, наприклад: 1) зменшуване 6, від’ємник 1, зайти значення різниці (6 – 1 = 5); 2) перший доданок 5, другий доданок 2, знайти значення суми (5 + 2 = 8); 3) зменшуване 10, від’ємник 2, знайти значення різниці (10 – 2 = 8). Також доцільно запропонувати школярам прочитати вирази з назвою компонентів та знайти їх значення. При обчисленні значень виразів пропонуємо в рівностях на віднімання підкреслити однією рискою зменшуване, двома - від'ємник, хвилястою лінією - значення різниці.
зменшуване
3 7 значення різниці від’ємник 10 – 7 = 3 Додавання і віднімання нуля. Віднімання однакових чисел. Після ознайомлення з числом нуль, учні вчаться виконувати додавання і віднімання з нулем. Ввести ці правила можна на підставі індуктивних узагальнень, пропонуючи учням проаналізувати кілька рівностей виду: 5 + 0 =5, 0 + 5 = 5, 5 – 0 = 5, 5 – 5 = 0. При Ці правила можна записати в загальному вигляді: а + 0 =0 + а = а, а – 0 = а, а – а = 0. Методика складання таблиць додавання і віднімання. Перед вивченням таблиць додавання і віднімання окремого числа (1,2...9) слід сформувати в учнів відповідні обчислювальні навички – цей найвищий ступінь оволодіння обчислювальними прийомами. Під прийомом обчислення розуміють систему операцій, яку потрібно виконати, щоб дія досягла своєї мети – це орієнтувальна основа дії (ООД). Таким чином, прийоми обчислення над числами складаються з ряду послідовних операцій (системи операцій), виконання яких призводить до знаходження відповіді арифметичної дії над цими числами, причому вибір операції в кожному прийомі встановлюється тими теоретичними положеннями, які використовуються як його теоретична основа.
Теоретичною основою додавання та віднімання 1 є знання порядку прямування чисел в натуральному ряді. Числа 2, 3, 4, 5 додають і віднімають частинами на підставі складу цих чисел (теоретична основа – правило додавання суми до числа). Переставний закон додавання є теоретичною основою прийому додавання чисел 6,7,8,9. Числа 6,7,8,9 віднімають на підставі взаємозв’язку між діями додавання і віднімання. Учні не повинні бездумно заучувати таблиці, вони мають знати спосіб обчислення і користуватися ним при знаходженні значень виразів. Тому спочатку формуємо відповідні обчислювальні навички і на останньому етапі складаємо таблиці. При ознайомленні і первинному закріпленні обчислювального прийому міркування подаються розгорнено і повністю промовляються вголос, потім вони поступово скорочуються і автоматизуються, в результаті чого учень набуває навичкиу виконанні даної дії. Виходячи із груп прийомів обчислення в межах 10 слід дотримуватися такого порядку опрацювання таблиць додавання і віднімання: 1) додавання і віднімання числа 1; 2) додавання і віднімання числа 2; 3) додавання і віднімання числа 3; 4) додавання і віднімання числа 4; узагальнення прийому додавання і віднімання по частинах; 5) додавання на підставі переставного закону додавання: додавання чисел 5,6,7,8,9; 6) віднімання на підставі взаємозв’язку дій додавання і віднімання: віднімання чисел 5,6,7,8,9. Розглянемо зміст обчислювальних прийомів.
8 8 9 9
3+6 Методика формування обчислювальних навичок передбачає етапи: 1) ознайомлення з прийомом обчислення, надання учням орієнтувальної основи дії; 2) виконання учнями нової дії, спираючись на матеріалізовані опори – картки з друкованою основою, пам’ятки; 3) розгорнене виконання дії з промовлянням уголос кожного кроку пам’ятки (спочатку читаючи кожне завдання пам’ятки, а потім – промовляючи своїми словами); 4) виконання дії з промовлянням „про себе” кроків пам’ятки; під час виконання дія скорочується – виконуються лише основні операції; 5) виконання дії в розумовому плані, дія максимально скорочується та автоматизується.
На останньому етапі складаємо таблиці. Збільшення або зменшення числа на кілька одиниць. Ознайомленняздійснюємо засобом виконання практичних вправ: 1. Покладіть на парту 5 жовтих квадратів. Покладіть під ними стільки ж червоних квадратів. Скільки треба покласти червоних квадратів? Покладіть поряд ще один червоний квадрат. Тепер квадратів стільки ж? (Ні. Червоних квадратів більше). На скільки червоних квадратів більше, ніж жовтих? (На 1). Розгляньте, як виконали схематичний малюнок. Яких квадратів більше? На скільки більше?
Червоних квадратів стільки ж, скільки й жовтих та ще 1. На 1 більше – це значить стільки ж та ще 1. Якою арифметичною дією знайдемо 5 та ще 1? (Дією додавання.) Складемо рівність: 5 + 1 = 6. Червоних квадратів 6. Щоб дізнатися про число, яке на 1 більше, треба додати! Аналогічно розглядаємо зменшення на 1. Розглядаємо, як зроблено схематичний малюнок:
   Стільки ж без 1 Стільки ж без 1
Учні дістають висновку: червоних квадратів стільки ж, скільки й жовтих але без 1. На 1 менше – це значить стільки ж, але без 1. Щоб дізнатися про число, яке на 1 менше, треба відняти!
В аналогічний спосіб можна познайомити учнів із різницевим порівнянням: – Скільки жовтих квадратів? Скільки червоних квадратів. Складіть пари. Яких квадратів більше? На скільки більше? Якою дією дізнаємось?
Коментар. Жовтих квадратів 4, а червоних 5; 4 менше 5-ти на 1, тому що не вистачило 1-го жовтого квадрата для складання пари; 5 більше 4-х на 1-му, тому що 1 червоному квадрату не вистачило пари. Щоб дізнатися, скільком квадратам не вистачило пари, треба відняти від числа червоних квадратів стільки ж квадратів, скільки й жовтих. Скільком вистачило пари? Отже, щоб дізнатися, на скільки одне число більше за інше, треба від більшого відняти менше. Зміна значення суми в залежності від зміни одного з доданків. Зміна значення різниці в залежності від зміни зменшуваного. При вивченні таблиць додавання існує можливість познайомити учнів спочатку з характером зміни значення суми в залежності від зміни одного з доданків: доданок і значення сума змінюються в одному напрямку. Потім перейти до формулювання правила: якщо перший доданок збільшиться (зменшиться) на кілька одиниць, то значення суми так само збільшиться (зменшиться) на стільки ж одиниць. При вивченні таблиць віднімання можна спочатку познайомити учнів із характером зміни значення різниці залежно від зміни зменшуваного: зменшуване і значення різниці змінюються в одному напрямку. Далі відбувається ознайомлення з правилом: якщо зменшуване збільшиться (зменшиться) на кілька одиниць, то й значення різниці так само збільшиться (зменшиться) на стільки ж одиниць.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.156.66 (0.016 с.) |

 – Прочитайте першу рівність: перший доданок 5, другий доданок 4, значення суми 9. Прочитайте другу рівність: перший доданок 4, другий доданок 5, значення суми 9. Що помітили? (Перший доданок став другим, а другий доданок став першим, значення суми від цього не змінилося...)
– Прочитайте першу рівність: перший доданок 5, другий доданок 4, значення суми 9. Прочитайте другу рівність: перший доданок 4, другий доданок 5, значення суми 9. Що помітили? (Перший доданок став другим, а другий доданок став першим, значення суми від цього не змінилося...) 3 2
3 2









 2 3 2 + 3 = 5
2 3 2 + 3 = 5
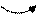 Доцільно познайомити учнів із застосуванням переставного закону у випадку трьох доданків і познайомити учнів з іншим його формулюванням: додавати числа можна в будь-якому порядку. Це правило дуже спрощує обчислення у випадках трьох доданків, коли значення суми двоцифрове число. Наприклад: 7+4+3=7+34 = =10 + 4 = 14
Доцільно познайомити учнів із застосуванням переставного закону у випадку трьох доданків і познайомити учнів з іншим його формулюванням: додавати числа можна в будь-якому порядку. Це правило дуже спрощує обчислення у випадках трьох доданків, коли значення суми двоцифрове число. Наприклад: 7+4+3=7+34 = =10 + 4 = 14 Взаємозв’язок між діями додавання і віднімання. Познайомити учнів з взаємозв’язком додавання і віднімання можна за допомогою наочного посібника:
Взаємозв’язок між діями додавання і віднімання. Познайомити учнів з взаємозв’язком додавання і віднімання можна за допомогою наочного посібника:
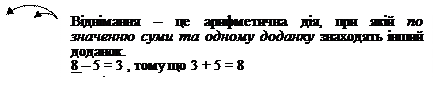
 8 – 3 = 5
8 – 3 = 5



 7
7 зменшуване
зменшуване
 Правила знаходження невідомого зменшуваного, невідомого від’ємника. Познайомити учнів з цими правилами можна через аналіз схематичного зображення компонентів та результату дії віднімання.
Правила знаходження невідомого зменшуваного, невідомого від’ємника. Познайомити учнів з цими правилами можна через аналіз схематичного зображення компонентів та результату дії віднімання.




 нуля
нуля 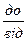 будь-якого числа в результаті отримаємо те ж саме число. При відніманні однакових чисел в результаті отримаємо нуль.
будь-якого числа в результаті отримаємо те ж саме число. При відніманні однакових чисел в результаті отримаємо нуль.

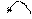
 + 1: наступне - 1: попереднє
+ 1: наступне - 1: попереднє

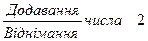
 + 2: +1 +1 - 2: -1 -1
+ 2: +1 +1 - 2: -1 -1






 + 3: +1 +2 - 3: -2 -1
+ 3: +1 +2 - 3: -2 -1
 + 2 +1 - 1 - 2
+ 2 +1 - 1 - 2


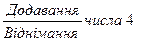


 +4: +1 +3 - 4: -3 -1
+4: +1 +3 - 4: -3 -1
 + 3 +1 - 1 - 3
+ 3 +1 - 1 - 3
 Додавання 5;6;7;8;9
Додавання 5;6;7;8;9
 5 5
5 5


 6 6
6 6









 Наприклад: 9 - 6 = 3 + 6 – 6 = 3
Наприклад: 9 - 6 = 3 + 6 – 6 = 3



 Формуємо поняття: якщо одне число на кілька одиниць більше іншого, то інше число, навпаки, менше на стільки ж одиниць.
Формуємо поняття: якщо одне число на кілька одиниць більше іншого, то інше число, навпаки, менше на стільки ж одиниць.






