
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гиперболический параболоид. Исследование формы гиперболоида по каноническому уравнению.Содержание книги
Поиск на нашем сайте
Гиперболический параболоид(седловая поверхность)-поверхность второго порядка, имеющая в канонической для неё декартовой прямоугольной системе координат уравнение α||XOY z=λ
β||XOZ y=μ
ɤ||YOZ x=
37. Пересечение поверхностей второго порядка. Пусть дано уравнение поверхности второго порядка: а11х2+а22у2+а33z2+2а12xy+2а13z+2а23yz+а14x+а24y+а34z+а44=0. (1)aij=aji.Пусть прямая задана координатно-параметрическим уравнением:
Рассмотрим совместно поверхность F и прямую m, где F- (1), а m- (2).
Подставляем значения x, y, z в уравнение поверхности второго порядка. После чего, собираем все в формулу: At2+Bt+C=0. (3). А≠0, имеем два корня t1,t2 à t1,≠t2,имеем две точки пересечения; t1,=t2- точка касания, слившиеся две точки; B=2а11аx0+2а22by0+2a33cz0+2a12(bx0+ay0)+2a13(cx0+az0)+2a23(cy0+bz0)+2a14a+2a24b+2a34c.C=a11x02+a22y02+a33z02+2a12x0y0+2a13x0z0+2a23y0z0+2a14x0+2a24y0+2a34z0+a44.A=0, имеем Bt+C=0 следует из уравнения (3).Имеем один корень t- одна точка пересечения(не касания). При В≠0.А если В=0, С≠0, то 38. Прямолинейные образующие однополостного гиперболоида. У однополостного гиперболоида есть два семейства прямолинейных образующих. Через каждую его точку проходит по семейству из каждого семейства.
1-ое семейство.
2-ое семейство.
При данных p и q система (2) определяет прямую l, перемножая левые и правые части уравнений системы (2) и сокращая на произведение pq (при условии, что pq≠0) получим в точности уравнение (1), следовательно любая точка прямой l ϵ гиперболоиду. Предположим, что pq=0, тогда по условию p=0, q≠0. Тогда, уравнения системы (2) дают:
Для случая p≠0, q=0 уравнения системы (2) дадут: Покажем, что через каждую точку гиперболоида проходит по одной прямой из семейств 1 и 2. Рассмотрим семейство 1. M0(x0,y0z0) ϵ гиперболоиду.
Задачей является подобрать соответствующие p и q. Если, в уравнение (5), хотя бы один из множителей при p и q отличен от 0, то можем положить q= Если же уравнение (5) сводится к равенству 0=0, то рассмотрим уравнение (6), и положим q=
39. Прямолинейные образующие гиперболического параболоида. У гиперболического параболоида есть два семейства прямолинейно-образующих. Через каждую точку гиперболического параболоида проходит по образующей из каждого семейства.
1-ое семейство.
2-ое семейство.
Рассмотрим прямую l ϵ 1-ому семейству. Подставляя второе уравнение в первое из системы (2) и сокращая на q в очности получим уравнение (1), т.е. для любого х, у удовлетворяющих второму уравнению системы (2) удовлетворяется и первое. Пусть точка M0(x0,y0z0) принадлежит гиперболоиду, положим в системе (2) p = Для семейства 2 определяемого системой (3), можно положить q|=
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 739; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.173.81 (0.008 с.) |

 называемое каноническим.
называемое каноническим. ; λ=0 пара ∩ дейст.прямых
; λ=0 пара ∩ дейст.прямых  ; λ< 0 à гипербола; λ> 0 -гипербола.
; λ< 0 à гипербола; λ> 0 -гипербола. Для любых μ
Для любых μ 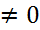 и μ=0- парабола
и μ=0- парабола
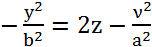 Для любого
Для любого  - парабола.
- парабола. (2) t-параметр, {a,b,c}-направляющие коорд. вектора в прямой. М0{x0,y0,z0}-коорд. нач.точки прямой
(2) t-параметр, {a,b,c}-направляющие коорд. вектора в прямой. М0{x0,y0,z0}-коорд. нач.точки прямой
 - не пересекаются.А=а11а2+а22b2+2a33c2+2a12ab+2a13ac+2a23bc.
- не пересекаются.А=а11а2+а22b2+2a33c2+2a12ab+2a13ac+2a23bc. à
à  à
à 
 (2)
(2) (3)
(3) , и тогда уравнение (1) выполнимо. Следовательно, вновь любая точка прямой l ϵ гиперболоиду.
, и тогда уравнение (1) выполнимо. Следовательно, вновь любая точка прямой l ϵ гиперболоиду. , и уравнение вновь удовлетвориться.
, и уравнение вновь удовлетвориться.

 ; p=
; p=  , и тогда подставляя полученное p и q в уравнение (6), в точности получим уравнение (1). И, следовательно, через точку M0 гиперболоида проходит прямая из 1-го семейства.
, и тогда подставляя полученное p и q в уравнение (6), в точности получим уравнение (1). И, следовательно, через точку M0 гиперболоида проходит прямая из 1-го семейства. ; p=
; p=  , заметим, что в данном случае (q≠0) так как
, заметим, что в данном случае (q≠0) так как  ; таким образом уравнение (5) при данных p и q сводится к уравнению (1). А уравнение (6) выполняется тождественно. И, соответственно, через точку М0 гиперболоида проходит прямая 1-го семейства. Для 2-го семейства доказывается аналогично.
; таким образом уравнение (5) при данных p и q сводится к уравнению (1). А уравнение (6) выполняется тождественно. И, соответственно, через точку М0 гиперболоида проходит прямая 1-го семейства. Для 2-го семейства доказывается аналогично.
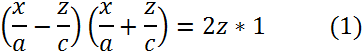
 (2)
(2) (3)
(3)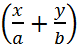 ; q=1, то второе уравнение системы будет выполняться тождественно, а первое в точности дает уравнение (1). И, следовательно, х=х0,у=у0,z=z0, оба уравнения системы (2) удовлетворяются, и, следовательно, через точку М гиперболоида, проходит прямая семейства 1.
; q=1, то второе уравнение системы будет выполняться тождественно, а первое в точности дает уравнение (1). И, следовательно, х=х0,у=у0,z=z0, оба уравнения системы (2) удовлетворяются, и, следовательно, через точку М гиперболоида, проходит прямая семейства 1. ; p|=1 и х=х0,у=у0,z=z0, система (3) удовлетворяется, проходит прямая семейства 2.
; p|=1 и х=х0,у=у0,z=z0, система (3) удовлетворяется, проходит прямая семейства 2.


