
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение поверхности в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Уравнение поверхности в пространстве. Пусть заданы декартова прямоугольная система координат Охуz в пространстве и некоторая поверхность S. Определение. Уравнение F(x;y;z)=0 (7) называется уравнением поверхности S (относительно заданной системы координат), если этому уравнению удовлетворяют координаты х,у, z любой точки, лежащей на поверхности S, и не удовлетворяют координаты х, y и z ни одной точки, не лежащей на поверхности S. Т.о. поверхностью называется геометрическое место точек {M(x;y;z)}, координаты которых удовлетворяют уравнению (7). Уравнение (7) определяет поверхность S. z=f(x;y) (8) – явное уравнение линии в ДСК (Уравнение (8) может быть получено из уравнения (7) путем выражения из этого уравнения одной переменной через другие.
x2+y2=R2 Пример. Уравнение сферы. Сферой в пространстве называется множество точек равноудаленных от заданной точки М0(х0;у0;z0) – центра сферы. Пусть М(х;у;z) – некоторая переменная точка сфера. Расстояние от точки М до центра М0 постоянно и равно радиусу сферы, т.е. d(M0M)=const=R R= R2=(x-x0)2+(y-y0)2+(z-z0)2 – уравнение сферы. Уравнения линия в пространстве R3. Линия в пространстве определяется как пересечение двух поверхностей, т.е. как геометрическое место точек, находящихся одновременно на двух поверхностях.
Линию как пересечение двух поверхностей в пространстве можно представить бесчисленным числом способов. Т.е. вместо системы (9) можно взять любую эквивалентную систему. Параметрические уравнения линии и поверхности в пространстве. Ли нию в пространстве можно так же задать параметрически:
Покажем, что этот способ определения линии в пространстве эквивалентен определению линии как пересечения двух поверхностей. Допустим, что хотя бы одна из трех функций, например c(t), имеет обратную. Тогда t=c-1(z) подставляя это значение вместо t в первые два равенства (10), получим уравнения двух поверхностей x=j(c-1(z)), y=y(c-1(z)), пересечением которых является данная линия. Пример (с.115). Классификация поверхностей. Определение 1. Поверхность называется алгебраической, если в некоторой декартовой прямоугольной системе координат, если она определяется алгебраическим уравнением F(x;y;z)=0 с тремя переменными. Определение 2. Всякая не алгебраическая поверхность называется трансцендентной. Определение 3. Алгебраическая поверхность называется поверхностью порядка n, если в некоторой декартовой прямоугольной системе координат она определяется алгебраическим уравнением степени n с тремя переменными. Установлению корректности определений 1,2,3 способствует следующая теорема. Теорема (док-во на с.117). Если поверхность в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени n, то эта поверхность и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени n. Плоскость в пространстве. Теорема. Любая плоскость в пространстве является поверхностью 1-го порядка и любая поверхность 1-го порядка вы пространстве есть плоскость. (т.е. плоскость задается уравнением 1-й степени с тремя переменными). Доказательство.
Вектор n =A i +B j +C k - нормальный вектор плоскости (вектор нормали). Множество всех точек пространства разбивается на три подмножества: точек, принадлежащих плоскости и точек, расположенных по одну и по другую стороны плоскости. Пусть М(х;у;z) – произвольная точка пространства. Какому из этих подмножеств принадлежит точка М зависит от знака скалярного произведения nM0M. Если точка М принадлежит плоскости, то M0M =(x-x0;y-y0;z-z0) A(x-x0)+B(y-y0)+C(z-z0)=0 причем А2+В2+С2¹0, т.к. вектор n – ненулевой. Преобразуем это уравнение: Ax+Ву+Сz-Аx0-By0-Cz0=0 Обозначим D=-Аx0-By0-Cz0 Ax+Ву+Сz+D=0 (1) – общее уравнение плоскости. Т.о. любой плоскости в пространстве соответствует уравнение первой степени относительно переменных х,у,z. Докажем 2-е утверждение, т.е. что при любом выборе параметров А, В и С уравнению (2) соответствует некоторая плоскость в пространстве. Зафиксируем произвольную декартову прямоугольную систему координат Охуz и рассмотрим произвольное уравнение первой степени с тремя переменными: Ax+Ву+Сz+D=0 (А2+В2+С2¹0) Это уравнение имеет хотя бы одно решение х0;у0;z0, т.е. существует хотя бы одна точка М0(х0;у0;z0), координаты которой удовлетворяют уравнению (1): Ax0+Ву0+Сz0+D=0 (2) Вычитая из уравнения (1) тождество (2), получим уравнение, эквивалентное (1): A(х-x0)+В(у-у0)+С(z-z0)+D=0 (3) Достаточно доказать, что уравнение (3) определяет относительно системы Охуz некоторую плоскость. Покажем, что уравнение (3), а значит и (1), определяет относительно системы Охуz плоскость p, проходящую через точку М0(х0;у0;z0) и перпендикулярную вектору n ={А;В;С} (т.к. А2+В2+С2≠0, то вектор n – ненулевой). Если точка М(х,у,z) лежит на плоскости p, то ее координаты удовлетворяют уравнению (3), т.к. в этом случае векторы n ={А;В;С} и Если же М(х,у,z) не лежит на плоскости p, то ее координаты не удовлетворяют уравнению (3), т.к. в этом случае векторы n ={А;В;С} и Ax+Ву+Сz+D=0 (1) (1) – общее уравнение плоскости. n ={А;В;С} – нормальный вектор плоскости. Замечание. Если два общих уравнения Ax+Ву+Сz+D=0 и А1х+В1у+С1z+D1=0 определяют одну и ту же прямую, то найдется такое число t, что A1=At, B1=Bt, C1=Ct, D1=Dt (4) Действительно, т.к. плоскости Ах+Ву+Сz+D=0 и А1х+В1у+С1z+D1=0 совпадают, то векторы n ={А;В;C} и n1 ={А1;В1;C1} коллинеарны, следовательно, по условию коллинеарности векторов, найдется такое число t, что n1 = n tÞиз линейного свойства координат вектора следуют первые три равенства (4). Т.к. плоскости совпадают, то они имеют общую точку М0(х0;у0;z0). Т.е. Ах0+Ву0+Сz0+D=0 и А1х0+В1у0+С1z0+D1=0. Вычитая из 2-го равенства 1-е, умноженное на t, получаем (At-А1)х0+(Bt-В1)у0+(Ct-С1)z0+(Dt-D1)=0ÞDt-D1=0ÞDt=D1. Т.о. общее уравнение плоскости, как и нормальный вектор плоскости, определяется с точностью до ненулевого числового множителя. Пучки и связки плоскостей. Определение. Совокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей (с центром в L). Теорема. (б.д.?)Если A1x+В1у+С1z+D1=0 и A2x+В2у+С2z+D2=0 уравнения двух различных непараллельных плоскостей, пересечением которых служит некоторая прямая L, а a и b - произвольные числа такие, что a2+b2¹0, то a(A1x+В1у+С1z+D1)+b(A2x+В2у+С2z+D2)=0 (15) уравнение плоскости, проходящей через прямую L. Какова бы ни была проходящая через прямую L плоскость, она определяется уравнением (15) при некоторых a и b. Определение. Совокупность всех плоскостей, проходящих через одну и ту же точку М0(х0;у0;z0), называется связкой плоскостей (с центром в М0). Уравнение связки с центром в точке М0(х0;у0;z0) имеет вид А(х-х0)+В(у-у0)+С(z-z0)=0 (16), где А2+В2+С2¹0 Прямая в пространстве. Связка прямых. Совокупность всех прямых, проходящих через точку М1(x1,y1,z1), называется связкой прямых (с центром в точке М1). Уравнения связки прямых с центром в точке М1 имеют вид:
где l, m, n - произвольные числа, такие, что l2+m2+n2¹0/ Действительно, всякая прямая, определяемая уравнениями (16), проходит через точку М1(x1,y1,z1). С другой стороны, если L – наперед заданная прямая, проходящая через точку М1(x1,y1,z1), то эта прямая однозначно определяется заданием, кроме точки М1(x1,y1,z1), направляющим вектором q ={l;m;n} и потому определяются каноническими уравнениями, совпадающими с уравнениями (16).
Уравнение поверхности в пространстве. Пусть заданы декартова прямоугольная система координат Охуz в пространстве и некоторая поверхность S. Определение. Уравнение F(x;y;z)=0 (7) называется уравнением поверхности S (относительно заданной системы координат), если этому уравнению удовлетворяют координаты х,у, z любой точки, лежащей на поверхности S, и не удовлетворяют координаты х, y и z ни одной точки, не лежащей на поверхности S. Т.о. поверхностью называется геометрическое место точек {M(x;y;z)}, координаты которых удовлетворяют уравнению (7). Уравнение (7) определяет поверхность S. z=f(x;y) (8) – явное уравнение линии в ДСК (Уравнение (8) может быть получено из уравнения (7) путем выражения из этого уравнения одной переменной через другие.
x2+y2=R2 Пример. Уравнение сферы. Сферой в пространстве называется множество точек равноудаленных от заданной точки М0(х0;у0;z0) – центра сферы. Пусть М(х;у;z) – некоторая переменная точка сфера. Расстояние от точки М до центра М0 постоянно и равно радиусу сферы, т.е. d(M0M)=const=R R= R2=(x-x0)2+(y-y0)2+(z-z0)2 – уравнение сферы. Уравнения линия в пространстве R3. Линия в пространстве определяется как пересечение двух поверхностей, т.е. как геометрическое место точек, находящихся одновременно на двух поверхностях.
Линию как пересечение двух поверхностей в пространстве можно представить бесчисленным числом способов. Т.е. вместо системы (9) можно взять любую эквивалентную систему. Параметрические уравнения линии и поверхности в пространстве. Ли нию в пространстве можно так же задать параметрически:
Покажем, что этот способ определения линии в пространстве эквивалентен определению линии как пересечения двух поверхностей. Допустим, что хотя бы одна из трех функций, например c(t), имеет обратную. Тогда t=c-1(z) подставляя это значение вместо t в первые два равенства (10), получим уравнения двух поверхностей x=j(c-1(z)), y=y(c-1(z)), пересечением которых является данная линия. Пример (с.115). Классификация поверхностей. Определение 1. Поверхность называется алгебраической, если в некоторой декартовой прямоугольной системе координат, если она определяется алгебраическим уравнением F(x;y;z)=0 с тремя переменными. Определение 2. Всякая не алгебраическая поверхность называется трансцендентной. Определение 3. Алгебраическая поверхность называется поверхностью порядка n, если в некоторой декартовой прямоугольной системе координат она определяется алгебраическим уравнением степени n с тремя переменными. Установлению корректности определений 1,2,3 способствует следующая теорема. Теорема (док-во на с.117). Если поверхность в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени n, то эта поверхность и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени n. Плоскость в пространстве. Теорема. Любая плоскость в пространстве является поверхностью 1-го порядка и любая поверхность 1-го порядка вы пространстве есть плоскость. (т.е. плоскость задается уравнением 1-й степени с тремя переменными). Доказательство.
Вектор n =A i +B j +C k - нормальный вектор плоскости (вектор нормали). Множество всех точек пространства разбивается на три подмножества: точек, принадлежащих плоскости и точек, расположенных по одну и по другую стороны плоскости. Пусть М(х;у;z) – произвольная точка пространства. Какому из этих подмножеств принадлежит точка М зависит от знака скалярного произведения nM0M. Если точка М принадлежит плоскости, то M0M =(x-x0;y-y0;z-z0) A(x-x0)+B(y-y0)+C(z-z0)=0 причем А2+В2+С2¹0, т.к. вектор n – ненулевой. Преобразуем это уравнение: Ax+Ву+Сz-Аx0-By0-Cz0=0 Обозначим D=-Аx0-By0-Cz0 Ax+Ву+Сz+D=0 (1) – общее уравнение плоскости. Т.о. любой плоскости в пространстве соответствует уравнение первой степени относительно переменных х,у,z. Докажем 2-е утверждение, т.е. что при любом выборе параметров А, В и С уравнению (2) соответствует некоторая плоскость в пространстве. Зафиксируем произвольную декартову прямоугольную систему координат Охуz и рассмотрим произвольное уравнение первой степени с тремя переменными: Ax+Ву+Сz+D=0 (А2+В2+С2¹0) Это уравнение имеет хотя бы одно решение х0;у0;z0, т.е. существует хотя бы одна точка М0(х0;у0;z0), координаты которой удовлетворяют уравнению (1): Ax0+Ву0+Сz0+D=0 (2) Вычитая из уравнения (1) тождество (2), получим уравнение, эквивалентное (1): A(х-x0)+В(у-у0)+С(z-z0)+D=0 (3) Достаточно доказать, что уравнение (3) определяет относительно системы Охуz некоторую плоскость. Покажем, что уравнение (3), а значит и (1), определяет относительно системы Охуz плоскость p, проходящую через точку М0(х0;у0;z0) и перпендикулярную вектору n ={А;В;С} (т.к. А2+В2+С2≠0, то вектор n – ненулевой). Если точка М(х,у,z) лежит на плоскости p, то ее координаты удовлетворяют уравнению (3), т.к. в этом случае векторы n ={А;В;С} и Если же М(х,у,z) не лежит на плоскости p, то ее координаты не удовлетворяют уравнению (3), т.к. в этом случае векторы n ={А;В;С} и Ax+Ву+Сz+D=0 (1) (1) – общее уравнение плоскости. n ={А;В;С} – нормальный вектор плоскости. Замечание. Если два общих уравнения Ax+Ву+Сz+D=0 и А1х+В1у+С1z+D1=0 определяют одну и ту же прямую, то найдется такое число t, что A1=At, B1=Bt, C1=Ct, D1=Dt (4) Действительно, т.к. плоскости Ах+Ву+Сz+D=0 и А1х+В1у+С1z+D1=0 совпадают, то векторы n ={А;В;C} и n1 ={А1;В1;C1} коллинеарны, следовательно, по условию коллинеарности векторов, найдется такое число t, что n1 = n tÞиз линейного свойства координат вектора следуют первые три равенства (4). Т.к. плоскости совпадают, то они имеют общую точку М0(х0;у0;z0). Т.е. Ах0+Ву0+Сz0+D=0 и А1х0+В1у0+С1z0+D1=0. Вычитая из 2-го равенства 1-е, умноженное на t, получаем (At-А1)х0+(Bt-В1)у0+(Ct-С1)z0+(Dt-D1)=0ÞDt-D1=0ÞDt=D1. Т.о. общее уравнение плоскости, как и нормальный вектор плоскости, определяется с точностью до ненулевого числового множителя.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3000; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

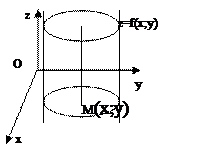 Если уравнение (7) не содержит какой-либо координаты х,у или z, то получаем уравнение цилиндрической поверхности, которая параллельна оси, соответствующей отсутствующей переменной. F(x;y)=0
Если уравнение (7) не содержит какой-либо координаты х,у или z, то получаем уравнение цилиндрической поверхности, которая параллельна оси, соответствующей отсутствующей переменной. F(x;y)=0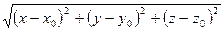
 (9) – общее уравнение линии в пространстве.
(9) – общее уравнение линии в пространстве. (10) где функции j(t), y(t) и c(t) определены и непрерывны в некотором промежутке изменения параметра t.
(10) где функции j(t), y(t) и c(t) определены и непрерывны в некотором промежутке изменения параметра t.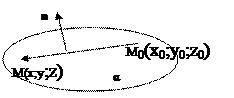 Найдем уравнение плоскости, проходящей через данную точку М0(х0;у0;z0) перпендикулярно заданному вектору.
Найдем уравнение плоскости, проходящей через данную точку М0(х0;у0;z0) перпендикулярно заданному вектору. n. Следовательно, n·M0M= 0. Т.е.
n. Следовательно, n·M0M= 0. Т.е. ={ х-х0;y-y0;z-z0} ортогональны и их скалярное произведение
={ х-х0;y-y0;z-z0} ортогональны и их скалярное произведение 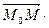 n =0 Þ (х-х0)А+(y-y0)В+(z-z0)С=0.
n =0 Þ (х-х0)А+(y-y0)В+(z-z0)С=0. (16)
(16)


