Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент силы. Уравнение динамики вращательного движения твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 25):
Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
где a— угол между r и F; r sina = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы. Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента Мz не зависит от выбора положения точки О на оси z.
Рис. 25 Рис. 26 Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:
Рис. 27 Найдем выражение для работы при вращении тела (рис. 27). Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, a — угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dj точка приложения В проходит путь d s=r dj и работа равна произведению проекции силы на направление смещения на величину смещения:
Учитывая (17.2), можем записать
где Fr sin a = Fl =Mz — момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но Учитывая, что
Уравнение (17.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Можно показать, что если ось z совпадает с главной осью инерции (см. § 19), проходящей через центр масс, то имеет место векторное равенство
где J — главный момент инерции тела (момент инерции относительно главной оси).
§ 18. Момент импульса и закон его сохранения При сравнении законов вращательного и поступательного движений просматривается аналогия между ними, только во вращательном движении вместо силы «выступает» ее момент, роль массы «играет» момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси.
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r — радиус-вектор, проведенный из точки О в точку A, p =m v — импульс материальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р. Модуль вектора момента импульса
где a — угол между векторами r и р, l — плечо вектора р относительно точки О. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.
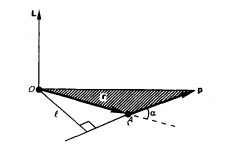
Рис. 28 При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой скоростью v i. Скорость v i и импульс mi v i перпендикулярны этому радиусу, т. с. радиус является плечом вектора mi v i. Поэтому можем записать, что момент импульса отдельной частицы равен
и направлен по оси в сторону, определяемую правилом правого винта. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
Используя формулу vi = wri, получим
т. е.
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцируем уравнение (18.2) по времени:
т. е.
Это выражение — еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Можно показать, что имеет место векторное равенство
В замкнутой системе момент внешних сил
Выражение (18.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Рис. 29
Табл.2
Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидящий на скамье, которая без трения вращается вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 29), приведен во вращение с угловой скоростью w1. Если человек прижмет гантели к себе, то момент инерции системы уменьшится. Поскольку момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения w2 возрастает. Аналогично, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения. Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (табл. 2).
§ 19. Свободные оси. Гироскоп Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис. 30). Для однородного цилиндра одной из главных осей инерции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоскости, перпендикулярной геометрической оси цилиндра. Главными осями инерции шара являются любые три взаимно перпендикулярные оси, проходящие через центр масс.
Рис. 30 Рис. 31
Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения тела. Можно показать, что вращение вокруг главных осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым. Так, если подбросить тело, имеющее форму параллелепипеда, приведя его одновременно во вращение, то оно, падая, будет устойчиво вращаться вокруг осей 1 и 2 (рис. 30). Если, например, палочку подвесить за один конец нити, а другой конец, закрепленный к шпинделю центробежной машины, привести в быстрое вращение, то палочка будет вращаться в горизонтальной плоскости около вертикальной оси, перпендикулярной оси палочки и проходящей через ее середину (рис. 31). Это и есть ось свободного вращения (момент инерции при этом положении палочки максимальный). Если теперь палочку, вращающуюся вокруг свободной оси, освободить от внешних связей (аккуратно снять верхний конец нити с крючка шпинделя), то положение оси вращения в пространстве в течение некоторого времени сохраняется. Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике. Наиболее интересны в этом плане гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью. Рассмотрим одну из разновидностей гироскопов — гироскоп на кардановом подвесе (рис. 32). Дискообразное тело — гироскоп — закреплено на оси АА, которая может вращаться вокруг перпендикулярной ей горизонтальной оси ВВ, которая, в свою очередь, может поворачиваться вокруг вертикальной оси DD. Все три оси пересекаются в одной точке С, являющейся центром масс гироскопа и остающейся неподвижной, а ось гироскопа может принять любое направление в пространстве. Силами трения в подшипниках всех трех осей и моментом импульса колец пренебрегаем.
Рис. 32 Рис. 33
Таккак трение в подшипниках мало, то, пока гироскоп неподвижен, его оси можно придать любое направление. Если начать гироскоп быстро вращать (например, с помощью намотанной на ось веревочки) и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной. Это можно объяснить с помощью основного закона динамики вращательного движения. Для свободно вращающегося гироскопа сила тяжести не может изменить ориентацию его свободной оси, так как эта сила приложена к центру масс (центр вращения С совпадает с центром масс), а момент силы тяжести относительно закрепленного центра масс равен нулю. Моментом сил трения мы также пренебрегаем. Поэтому если момент внешних сил относительно его закрепленного центра масс равен нулю, то, как следует из уравнения (19.3), L = const. т. е. момент импульса гироскопа сохраняет свою величину и направление в пространстве. Следовательно, вместе с ним сохраняет свое положение в пространстве и ось гироскопа. Чтобы ось гироскопа изменила свое направление в пространстве, необходимо, согласно (18.3), отличие от нуля момента внешних сил. Если момент внешних сил, приложенных к вращающемуся гироскопу, относительно его центра масс отличен от нуля, то наблюдается явление, получившее название гироскопического эффекта. Оно состоит в том, что под действием пары сил F, приложенной к оси вращающегося гироскопа, ось гироскопа (рис. 33) поворачивается вокруг прямой О 3 О 3, а не вокруг прямой O 2 O 2, как это казалось бы естественным на первый взгляд (O 1 O 1 и O 2 O 2 лежат в плоскости чертежа, а О 3 О 3 и силы F перпендикулярны ей). Гироскопический эффект объясняется следующим образом. Момент М пары сил F направлен вдоль прямой О 2 О 2. За время d t момент импульса L гироскопа получит приращение d L = M d t (направление d L совпадает с направлением М) и станет равным L '= L +d L. Направление вектора L ' совпадает с новым направлением оси вращения гироскопа. Таким образом, ось вращения гироскопа повернется вокруг прямой О 3 О 3. Если время действия силы мало, то, хотя момент сил М и велик, изменение момента импульса d L гироскопа будет также весьма малым. Поэтому кратковременное действие сил практически не приводит к изменению ориентации оси вращения гироскопа в пространстве. Для ее изменения следует прикладывать силы в течение длительного времени.
Если ось гироскопа закреплена подшипниками, то вследствие гироскопического эффекта возникают так называемые гироскопические силы, действующие на опоры, в которых вращается ось гироскопа. Их действие необходимо учитывать при конструировании устройств, содержащих быстровращающиеся массивные составные части. Гироскопы применяются в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т. д.). Другое важное применение гироскопов — поддержание заданного направления движения транспортных средств, например судна (авторулевой) и самолета (автопилот) и т. д. При всяком отклонении от курса вследствие каких-то воздействий (волны, порыва ветра и т. д.) положение оси гироскопа в пространстве сохраняется. Следовательно, ось гироскопа вместе с рамами карданова подвеса поворачивается относительно движущегося устройства. Поворот рам карданова подвеса с помощью определенных приспособлений включает рули управления, которые возвращают движение к заданному курсу. Впервые гироскоп применен французским физиком Ж. Фуко (1819—1868) для доказательства вращения Земли.
Деформации твердого тела Рассматривая механику твердого тела, мы пользовались понятием абсолютно твердого тела. Однако в природе абсолютно твердых тел нет, так как все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются. Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными). Деформации реального тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь и рассматривать упругие деформации, что мы и будем делать. В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения или сжатия и сдвига.
Рис.34
Рассмотрим однородный стержень длиной l и площадью поперечного сечения S (рис. 34), к концам которого приложены направленные вдоль его оси силы F 1 и F 2 (F 1 =F 2 =F), в результате чего длина стержня меняется на величину D l. Естественно, что при растяжении D l положительно, а при сжатии отрицательно. Сила, действующая на единицу площади поперечного сечения, называется напряжением:
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности — тангенциальным. Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация. Так, относительное изменение длины стержня (продольная деформация)
относительное поперечное растяжение (сжатие)
где d — диаметр стержня. Деформации e и e' всегда имеют разные знаки (при растяжении D l положительно, a D d отрицательно, при сжатии D l отрицательно, a D d положительно). Из опыта вытекает взаимосвязь e и e':
где m — положительный коэффициент, зависящий от свойств материала и называемый коэффициентом Пуассона. Английский физик Р. Гук (1635—1703) экспериментально установил, что для малых деформаций относительное удлинение e и напряжение s прямо пропорциональны друг другу:
где коэффициент пропорциональности Е называется модулем Юнга. Из выражения (20.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице. Из формул (20.2), (20.3) и (20.1) вытекает, что
или
где k— коэффициент упругости. Выражение (20.4) также задает закон Гука, согласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.
Рис. 35 Рис. 36
Деформации твердых тел подчиняются закону Гука до известного предела. Связь между деформацией и напряжением представляется в виде диаграммы напряжений, качественный ход которой мы рассмотрим для металлического образца (рис. 35). Из рисунка видно, что линейная зависимость s(e), установленная Гуком, выполняется лишь в очень узких пределах до так называемого предела пропорциональности (sп). При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость s(e) уже нелинейная) и до предела упругости (sу) остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, а параллельной ей — CF. Напряжение, при котором появляется заметная остаточная деформация (»0,2%), называется пределом текучести (sт) — точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, для которых же она практически отсутствует — хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности (sр). Диаграмма напряжений для реальных твердых тел зависит от различных факторов. Одно и то же твердое тело может при кратковременном действии сил проявлять себя как хрупкое, а при длительных, но слабых силах является текучим. Вычислим потенциальную энергию упруго растянутого (сжатого) стержня, которая равна работе, совершаемой внешними силами при деформации:
где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до D l. Согласно закону Гука (21.4), F=kx=ESx/l. Поэтому
т. е. потенциальная энергия упруго растянутого стержня пропорциональна квадрату деформации (D l)2. Деформацию сдвига проще всего осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу Ft , (рис. 36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется из формулы
где D s — абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между слоями (для малых углов tgg»g).
Глава 5.Тяготение. Элементы теории поля § 21. Законы Кеплера. Закон всемирного тяготения Еще в глубокой древности было замечено, что в отличие от звезд, которые неизменно сохраняют свое взаимное расположение в пространстве в течение столетий, планеты описывают среди звезд сложнейшие траектории. Для объяснения петлеобразного движения планет древнегреческий ученый К. Птолемей (II в. н. э.), считая Землю расположенной в центре Вселенной, предположил, что каждая из планет движется по малому кругу (эпициклу), центр которого равномерно движется по большому кругу, в центре которого находится Земля. Эта концепция получила название птолемеевой геоцентрической системы мира. В начале XVI в. польским астрономом Н. Коперником (1473—1543) обоснована гелиоцентрическая система (см. § 5), согласно которой движения небесных тел объясняются движением Земли (а также других планет) вокруг Солнца и суточным вращением Земли. Теория и наблюдения Коперника воспринимались как занимательная фантазия. К началу XVII столетия большинство ученых убедилось, однако, в справедливости гелиоцентрической системы мира. И. Кеплер (1571—1630), обработав и уточнив результаты многочисленных наблюдений датского астронома Т. Браге (1546—1601), изложил законы движения планет: 1. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. 2. Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади. 3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. Впоследствии И. Ньютон, изучая движение небесных тел, на основании законов Кеплера и основных законов динамики открыл всеобщий закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (m 1 и т 2) и обратно пропорциональная квадрату расстояния между ними (r 2):
Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитационной постоянной. Закон всемирного тяготения установлен для тел, принимаемых за материальные точки, т. е. для таких тел, размеры которых малы по сравнению с расстоянием между ними. Если же размеры взаимодействующих тел сравнимы с расстоянием между ними, то эти тела надо разбить на точечные элементы, подсчитать по формуле (21.1) силы притяжения между всеми попарно взятыми элементами, а затем геометрически их сложить (проинтегрировать), что является довольно сложной математической задачей. Впервые экспериментальное доказательство закона всемирного тяготения для земных тел, а также числовое определение гравитационной постоянной G проведено английским физиком Г. Кавендишем (1731—1810). Принципиальная схема опыта Кавендиша, применившего крутильные весы, представлена на рис. 37. Легкое коромысло А с двумя одинаковыми шариками массой m =729 г подвешено на упругой нити В. На коромысле С укреплены на той же высоте массивные шары массой M =158 кг. Поворачивая коромысло С вокруг вертикальной оси, можно изменять расстояние между шарами с массами т и М. Под действием пары сил, приложенных к шарам т со стороны шаров М, коромысло А поворачивается в горизонтальной плоскости, закручивая нить В до тех пор, пока момент сил упругости не уравновесит момента сил тяготения. Зная упругие свойства нити, по измеренному углу поворота можно найти возникающие силы притяжения, а таккак массы шаров известны, то и вычислить значение G.
Рис. 37
Значение G, приводимое в таблицах фундаментальных физических постоянных, принимается равным 6,6720×10–11 Н×м/кг2, т. е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,6720×10–11 H. Очень малая величина G показывает, что сила гравитационного взаимодействия может быть значительной только в случае больших масс.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 2664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.157.86 (0.017 с.) |

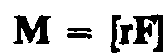
 (17.1)
(17.1)


 (17.2)
(17.2)
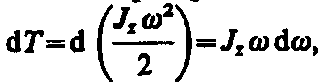 поэтому Mz dj = Jzw d w, или
поэтому Mz dj = Jzw d w, или 
 получаем
получаем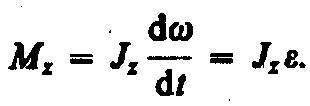 (17.3)
(17.3) (17.4)
(17.4)

 (18.1)
(18.1)
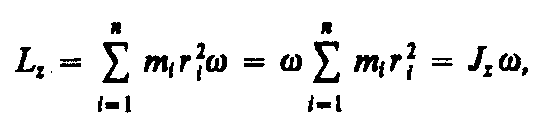
 (18.2)
(18.2)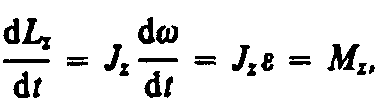

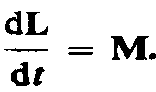 (18.3)
(18.3) откуда
откуда (18.4)
(18.4)




 (20.1)
(20.1) (20.2)
(20.2)

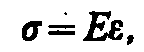 (20.3)
(20.3)
 (20.4)
(20.4)

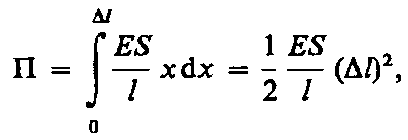
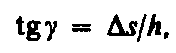
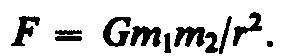 (21.1)
(21.1)