Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика вращательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для описания и исследования вращательного движения физические характеристики, которые были определены для поступательного движения (линейная скорость и ускорение, масса, сила, импульс), малоэффективны или даже непригодны (рис.18). Поэтому для вращательного движения устанавливают аналогичные величины, которые называются так же, как при поступательном движении, только с добавлением слов «угловая» или «момент». Тогда, чтобы получить закономерности вращательного движения, достаточно во всех предыдущих формулах физические величины поступательного движения заменить аналогичными величинами вращательного движения. Например, второй закон динамики для вращательного движения можно легко получить из такого же закона для поступательного движения, если силу заменить моментом силы, массу заменить моментом инерции (моментом массы), а линейное ускорение - угловым ускорением.
Угловая скорость и угловое ускорение Вращательное движение твердого тела принято характеризовать угловыми величинами, одинаковыми (в отличие от линейных скоростей Угловой скоростью (
его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности (правило правого винта, или правило правой руки) (рис.19). Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения. Размерность [ω]=сек−1, а единица измерения − радиан на секунду. Линейная скорость вращающей точки:
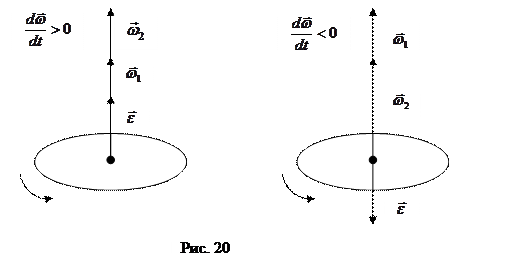
Учитывая правило правой руки При равномерном вращении ( Угловое ускорение – это быстрота изменения угловой скорости. Его модуль равен первой производной угловой скорости по времени или второй производной поворота угла по времени.
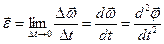
Вектор
Момент инерции, момент силы, момент импульса.
Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.
Момент инерции – мера инертности тела при вращательном движении. [6] Следует отметить, что момент инерции, являясь аналогом массы в классическом понимании, в отличие от нее, не является постоянной величиной и зависит от условия вращения (рис.21). Момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс c тела, сложенному с произведением массы m тела на квадрат расстояния a между осями (теорема Штейнера)
Кинетическую энергию вращения  можно получить, если в выражении кинетической энергии поступательного движения ( можно получить, если в выражении кинетической энергии поступательного движения ( ) заменить массу на момент инерции, а линейную скорость ) заменить массу на момент инерции, а линейную скорость 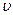 - на угловую скорость - на угловую скорость 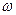 , ( , (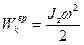 , где Jz момент инерции тела относительно оси z). , где Jz момент инерции тела относительно оси z).
Момент силы (вращающий момент) относительно неподвижной точки О –это векторное произведение радиуса вектора
 направление направление  определяется по правилу правой руки. определяется по правилу правой руки.
где Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора Если z совпадает с Используя аналоговый подход, для элементарной работы при вращении абсолютного твердого тела получаем Моментом импульса (количества движения ) материальной точки А относительно неподвижной точки О называется векторная величина
Иногда в некоторых книгах моментом импульса называется векторная величина Для отдельной материальной точки
Таким образом, формулы Можно показать, что имеет место и векторное выражение:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.223 (0.008 с.) |


 и ускорения
и ускорения  ) в данный момент времени для всех точек вращающегося твердого тела.
) в данный момент времени для всех точек вращающегося твердого тела. ), называется предел отношения угла поворота радиуса R (т. е. отношения углового пути
), называется предел отношения угла поворота радиуса R (т. е. отношения углового пути 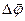 ) к промежутки времени
) к промежутки времени 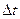 , за который этот поворот произошел, при стремлении промежутка времени к нулю. А это не что иное, как первая производная углового пути по времени.
, за который этот поворот произошел, при стремлении промежутка времени к нулю. А это не что иное, как первая производная углового пути по времени. 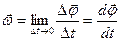 .
.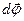 − псевдовектор, или аксиальный вектор, т. е. вектор, который направлен вдоль оси вращения. Модуль
− псевдовектор, или аксиальный вектор, т. е. вектор, который направлен вдоль оси вращения. Модуль 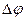 или
или  ), а
), а
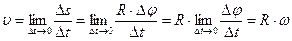 , так как
, так как 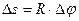 и R= const.
и R= const.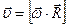 , (рис.19).
, (рис.19).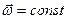 ) для описания вращательного движения определяют следующие параметры: период вращения T – это время, за которое тело совершает один полный оборот (т. е.
) для описания вращательного движения определяют следующие параметры: период вращения T – это время, за которое тело совершает один полный оборот (т. е. 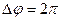 ), и частота вращения (
), и частота вращения (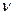 или n) – это число полных (или не полных) оборотов в единицу времени:
или n) – это число полных (или не полных) оборотов в единицу времени: 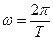 =
= 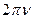
 направлен по
направлен по 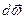 , когда угловая скорость растет,
, когда угловая скорость растет, 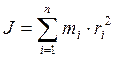 или для непрерывного распределения масс (физических тел)
или для непрерывного распределения масс (физических тел)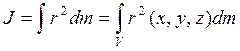
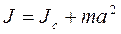

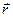 , проведенного из точки О в точку А приложения силы, на силу
, проведенного из точки О в точку А приложения силы, на силу  (рис. 22).
(рис. 22).
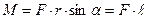 ,
,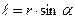 - кратчайшее расстояние между
- кратчайшее расстояние между 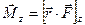 .
.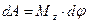 , где Mz − момент сил относительно оси z. А второй закон Ньютона для вращательного движения, или уравнение динамики вращательного движения твердого тела, примет вид
, где Mz − момент сил относительно оси z. А второй закон Ньютона для вращательного движения, или уравнение динамики вращательного движения твердого тела, примет вид 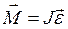 или
или 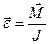 ; угловое ускорение вращательного движения прямо пропорционально суммарному моменту сил, приложенных к телу, и обратно пропорционально моменту инерции тела относительно оси вращения.
; угловое ускорение вращательного движения прямо пропорционально суммарному моменту сил, приложенных к телу, и обратно пропорционально моменту инерции тела относительно оси вращения.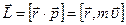 .
.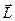 - псевдовектор, направление которого также определяется правилом правой руки (рис. 23).
- псевдовектор, направление которого также определяется правилом правой руки (рис. 23).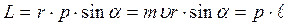
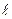 - плечо вектора p относительно точки O.
- плечо вектора p относительно точки O.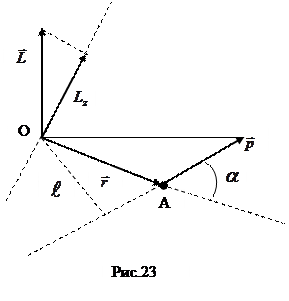 Моментом импульса относительно неподвижной оси Z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси.
Моментом импульса относительно неподвижной оси Z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси.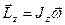 .
.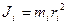 , тогда
, тогда (для твердого тела берем сумму всех материальных точек).
(для твердого тела берем сумму всех материальных точек).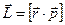 и
и  можно получить друг от друга. Отсюда
можно получить друг от друга. Отсюда 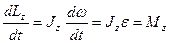 , т.е.
, т.е. 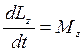 Это еще одна форма уравнения динамики вращательного движения твердого тела.
Это еще одна форма уравнения динамики вращательного движения твердого тела.