
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Е) направлен по касательной к траектории в сторону движения.
************************************* 69.1 Чему равна скорость при координатном способе задания движения точки В) ************************************* 70.1 Как определяются проекции скорости точки на неподвижные оси декартовых координат А) ************************************* 71.1 Как определить угол между вектором скорости и координатной осью 0х В) ************************************* 71.2 Как определить угол между вектором скорости и координатной осью 0у С) ************************************* 72.1 Направление вектора скорости относительно координатных осей находим В) по направляющим косинусам; 73.1 Что такое ускорение? B) Изменение скорости за единицу времени. ************************************* 74.1 Чему равны проекции ускорения на неподвижные координатные оси х и у. В) ************************************* 75.1 Что характеризует нормальное ускорение? D) изменение вектора скорости по направлению; ************************************* 76.1 Что характеризует касательное ускорение? D) изменение вектора скорости по направлению; ************************************* 77.1 Как вычислить полное ускорение при координатном способе задания движения точки? Е) ************************************* 77.2 Как вычислить касательное ускорение при координатном способе задания движения точки? В) ************************************* 77.3 Как вычислить нормальное ускорение при координатном способе задания движения точки? Е) ************************************* 78.1 Сумма углов между вектором скорости и координатными осями составляет C) 900; ************************************* 79.1 Закон движения точки при координатном способе задания В) ************************************* 79.2 Закон движения точки при естественном способе задания А) ************************************* 79.3 Закон движения точки при векторном способе задания С) ************************************* 80.1 Как вычислить нормальное ускорение при естественном способе задания движения точки? А) ************************************* 81.1 Как найти радиус кривизны траектории? Е) ************************************* 82.1 Чему равно полное ускорение точки при известных касательном и нормальном ускорении С) ************************************* 82.2 Чему равно полное ускорение точки при известных касательном и нормальном ускорении в векторном выражении. С) ************************************* 83.1 Как вычислить касательное ускорение при естественном способе задания движения точки? D) *************************************
84.1 Чему равно нормальное ускорение при прямолинейном движении. Е) 0. ************************************* 85.1 Автомобиль движется по горизонтальной дороге с постоянной скоростью ************************************* 85.2 Автомобиль движется по горизонтальной дороге с постоянной скоростью ************************************* 85.3 Автомобиль движется по горизонтальной дороге с постоянной скоростью ************************************* 85.4 Автомобиль движется по горизонтальной дороге с постоянной скоростью ************************************* 85.5 Автомобиль движется по горизонтальной дороге с постоянной скоростью ************************************* 86.1 Точка движется с постоянной скоростью ************************************* 86.2 Точка движется с постоянной скоростью ************************************* 87.1 Точка движется по криволинейной траектории с касательным ускорением ************************************* 88.1 Даны нормальное ************************************* 89.1 При поступательном движении; D) Траектории, скорости, ускорения всех точек объекта одинаковы; ************************************* 90.1 при поступательном движении машины со скоростью 20 км/ч, запасное колесо движется со скоростью B) 20; *************************************
************************************* 91.2 Объект 3, установленный на двух цилиндрических катках 1 и 2, совершает поступательное движение. Чему равно ускорение точки С, если ускорение точки А равно ************************************* 91.3 Объект 3, установленный на двух цилиндрических катках 1 и 2, совершает поступательное движение. Чему равно ускорение точки С, если ускорение точки А равно ************************************* 91.4 Объект 3, установленный на двух цилиндрических катках 1 и 2, совершает поступательное движение. Чему равно ускорение точки С, если ускорение точки А равно ************************************* 91.5 Объект 3, установленный на двух цилиндрических катках 1 и 2, совершает поступательное движение. Чему равно ускорение точки С, если ускорение точки А равно ************************************* 92.1 При прямолинейном замедленном движении объекта, как вектор скорости расположен: C) Лежит на одной прямой и противоположен по направлению вектору ускорения. ************************************* 92.2 При прямолинейном ускоренном движении объекта, как вектор скорости расположен: B) Лежит на одной прямой и совпадает по направлению с вектором ускорения. 93.1 1 При криволинейном движении точки вектор скорости и вектор нормального ускорения расположены: B) Перпендикулярны друг другу. ************************************* 94.1 Как направлен вектор нормального ускорения точки? B) По радиусу к центру кривизны. ************************************* 95.1 Закон движения при неравномерном движении точки. В) ************************************* 95.2 Закон движения при равномерном движении точки. Е) ************************************* 95.3 Закон движения при равнопеременном движении точки? С) ************************************* 96.1 Чему равна скорость при неравноменном движении? В) ************************************* 96.2 Чему равна скорость при равноменном движении? С) 96.3 Чему равна скорость при равнопеременном движении? Е) ************************************* 97.1 Чему равно ускорение при неравномерном движении С) ************************************* 97.2 Чему равно ускорение при равномерном движении А) ************************************* 97.3 Чему равно ускорение при равнопеременном движении С) ************************************* 97.4 Чему равно касательное ускорение при равномерном движении В) 0. ************************************* 97.5 Чему равно нормальное ускорение при равномерном движении А) ************************************* 97.6 Чему равно ускорение при прямолинейном равномерном движении Е) 0. ************************************* 98.1 Единица измерения линейного перемещения. C) м; ************************************* 98.2 Единица измерения линейной скорости. D) м/с; ************************************* 98.3 Единица измерения линейного ускорения. E) м/с2. ************************************* 98.4 Единица измерения касательного ускорения. E) м/с2. ************************************* 98.5 Единица измерения нормального ускорения. E) м/с2. ************************************* 99.1 Формула перевода углового перемещения в радианах в количество оборотов С) ************************************* 100.1 Закон вращательного движения при неравномерном вращении объекта А) ************************************* 100.2 Закон вращательного движения при равномерном движении объекта D) ************************************* 100.3 Закон вращательного движения при равнопеременном движении объекта С) ************************************* 101.1 Угловая скорость при неравномерном вращении объекта. С) *************************************
101.2 Угловая скорость при равномерном вращении объекта. С) ************************************* 101.3 Угловая скорость при равнопеременном вращении объекта. D) ************************************* 102.1 Угловое ускорение при неравномерном вращении объекта. D) ************************************* 102.2 Угловое ускорение при равномерном вращении объекта. A) 0. ************************************* 102.3 Угловое ускорение при равнопеременном вращении объекта. B) ************************************* 103.1 Касательное ускорение точки при равномерном вращении объекта. A) 0. 104.1 Полное ускорение точки при равномерном вращении объекта. A) 0. ************************************* 104.2 Полное ускорение при равнопеременном вращении объекта. C) ************************************* 105.1 Зависимость линейной скорости точки от угловой скорости вращения объекта вокруг неподвижной оси, при расположении точки на расстоянии Е) ************************************* 106.1 Как направлены векторы угловой скорости и углового ускорения С) вдоль оси вращения ************************************* 107.1 Формула перевода угловой скорости рад/сек в об/мин. В) ************************************* 108.1 Зависимость касательного ускорения точки от углового ускорения при вращении объекта вокруг неподвижной оси. В) ************************************* 108.2 Зависимость нормального ускорения точки от угловой скорости при вращении объекта вокруг неподвижной оси. D) ************************************* 109.1 Что такое угловая скорость? B) Угол поворота объекта за единицу времени. ************************************* 109.2 Что такое угловое ускорение? C) Изменение угловой скорости за единицу времени. ************************************* 110.1 Единица измерения углового перемещения. A) рад; ************************************* 110.2 Единицы измерения угловой скорости. D) рад/с; ************************************* 110.3 Единицы измерения углового ускорения E) рад/с2. ************************************* 111.1 3600 это: B) 1 оборот; ************************************* 111.2 ************************************* 111.3 1 оборот колеса это: B) ************************************* 112.1 Основная теорема кинематики В) ************************************* 113.1 Как определить абсолютную скорость при сложном движении точки. С) 113.2 Как определить абсолютное ускорение при сложном движении точки. В) ************************************* 113.3 Как определить кориолисово ускорение при сложном движении точки Е) ************************************* 113.4 Как определить кориолисово ускорение при сложном движении точки. Е) ************************************* 114.1 Единица измерения Кориолисова ускорения. E) м/с2.
************************************* 115.1 Чему равно кориолисово ускорение точки при поступательном переносном движении ************************************* 115.2 Чему равно кориолисово ускорение закрепленной точки на объекте при вращении объекта ************************************* 116.1 Если вектор угловой скорости при переносном движении параллелен вектору относительной скорости, то Кориолисово ускорение равно: A) 0; ************************************* 116.2 Если вектор угловой скорости при переносном движении параллелен вектору относительной скорости, то угол между векторами равен: A) 00; ************************************* 117.1 Если угол между векторами переносной угловой скорости и относительной скорости равен 00, то A) векторы параллельны; ************************************* 117.2 Если ************************************* 118.1 (Кориолисово ускорение равно нулю, если A) ************************************* 118.2 Кориолисово ускорение равно нулю, если A) ************************************* 118.3 Кориолисово ускорение равно нулю, если синус угла между векторами переносной угловой скорости и относительной скорости равен: A) ************************************* 119.1 Что такое мгновенный центр скоростей? A) Точка пространства, в которой в данный момент времени скорость как минимум двух точек объекта равны нулю. ************************************* 120.1 Если известны направления векторов скоростей двух точек, то мгновенный центр скоростей находится: B) На пересечении перпендикуляров к этим векторам; *************************************
121.1 Стержень ************************************* 122.1 Скорость центра катящегося по плоскости колеса радиуса 123.1 где находится мгновенный центр скоростей катящегося колеса по горизонтальной плоскости? B) В точке касания колеса с плоскостью. ************************************* 124.1 Основной закон динамики С) ************************************* 125.1 Уравнение движения объекта, движущегося поступательно Е) ************************************* 126.1 Уравнение движения объекта, вращающегося вокруг неподвижной оси А) ************************************* 127.1 Основное уравнение динамики: C) ************************************* 127.2 Основное уравнение динамики в проекциях на координатные оси D) ************************************* 127.3 Основное уравнение динамики в проекциях на естественные оси. E) ************************************* 127.4 Основное уравнение динамики в дифференциальной форме в проекциях на координатные оси. B) ************************************* 128.1 Что является движущим фактором, при поступательном движении объекта? B) Сила. ************************************* 128.2 Что является движущим фактором, при вращении объекта вокруг неподвижной оси? C) Скорость. ************************************* 129.1 Каков физический смысл понятия масса материального объекта? C) Это мера инертности объекта, характеризующая его способность воспринимать ускорение под действием приложенной к нему внешней силы.
************************************* 130.1 Укажите формулу теоремы о движении центра масс. A) ************************************* 131.1 Нормальная составляющей силы A) ************************************* 131.2 Нормальная составляющей силы A) ************************************* 131.3 Нормальная составляющей силы A) ************************************* 132.1 Касательная составляющей силы B) ************************************* 132.2 Касательная составляющей силы B) ************************************* 132.3 Касательная составляющей силы B) ************************************* 133.1 Сила в проекциях на координатные оси. C) ************************************* 133.2 Сила в проекциях на естественные оси. D) ************************************* 133.3 Сила в векторной форме E) ************************************* 134.1 Крутящий момент A) ************************************* 135.1 Единицы измерения крутящегося момента D) ************************************* 136.1 Метод кинетостатики в математическом выражении. A) ************************************* 137.1 Силы инерции возникает: B) При движении объекта с ускорением. ************************************* 138.1 Вектор силы инерции и вектор ускорения направлены B) По одной прямой в противоположные стороны; ************************************* 138.2 Векторa B) По одной прямой в противоположные стороны; ************************************* 138.3 Векторa B) По одной прямой в противоположные стороны; ************************************* 139.1 Сила инерции C) ************************************* 139.2 Сила инерции A) ************************************* 140.1 Расшифруйте единицу измерения силы Ньютон A) ************************************* 141.1 С какой целью в плоских механизмах для звеньев, движущихся плоско параллельно определяются ускорения их центров масс? D) Для определения величины и направления сил инерции при динамическом анализе механизмов. ************************************* 142.1 Что такое работа? C) Произведение силы на расстояние. ************************************* 143.1 Единицы измерения работы Е) ************************************* 144.1 Расшифруйте единицу измерения работы Джоуль C) ************************************* 145.1 Работа сил трения В) ************************************* 145.2 Работа сил при вращении объекта вокруг неподвижной оси. С) ************************************* 145.3 Работа сил при перемещении объекта на расстояние Е) ************************************* 145.4 Работа сил упругости D) ************************************* 145.5 Работа сил тяжести А) ************************************* 145.6 Работа сил сопротивления C) Всегда отрицательна. ************************************* 146.1 Если угол между вектором силы и перемещением равен ************************************* 146.2 Если угол между вектором силы и перемещением равен ************************************* 146.3 Если угол между вектором силы и перемещением равен ************************************* 146.4 Если угол между вектором силы и перемещением равен 147.1 Давление силы на площадь рассчитывается как: B) ************************************* 148.1 Давление измеряется: C) ************************************* 149.1 Расшифруйте единицу измерения давления Паскаль B) ************************************* 150.1 1 МПа это: E) 106Па. ************************************* 151.1 В чем измеряется коэффициент трения скольжения: E) Безразмерная величина. ************************************* 151.2 В чем измеряется коэффициент трения качения? C) ************************************* 152.1 Коэффициент трения качения это: C) Расстояние, на которое смещена результирующая реакция опорной поверхности упругого колеса от вертикальной оси колеса. ************************************* 153.1 В чем измеряется жесткость пружины? E) ************************************* 154.1 Что такое мощность? A) Работа, выполненная за единицу времени. ************************************* 155.1 Мощность сил сопротивления C) Всегда отрицательна. ************************************* 156.1 Единицы измерения мощности B) ************************************* 157.1 Мощность сил при поступательном движении объекта В) ************************************* 157.2 Мощность сил при поступательном движении объекта B) Произведение силы на скорость; ************************************* 158.1 Мощность сил при вращательном движении объекта вокруг неподвижной оси. В) ************************************* 158.2 Мощность сил при вращательном движении объекта вокруг неподвижной оси. B) Произведение крутящего момента на угловую скорость; ************************************* 159.1 Расшифруйте единицу измерения мощности Ватт B) ************************************* 160.1 Коэффициент полезного действия последовательно соединенных механизмов В) ************************************* 160.2 Коэффициент полезного действия D) ************************************* 161.1 Коэффициент полезного действия показывает А) потери на трение; *************************************
************************************* 162.2 На поршень гидроцилиндра действует сила ************************************* 162.3 На поршень гидроцилиндра действует сила ************************************* 162.4 На поршень гидроцилиндра действует сила ************************************* 162.5 На поршень гидроцилиндра действует сила *************************************
************************************* 163.2 К диску диаметра ************************************* 163.3 К диску диаметра ************************************ 163.4 К диску диаметра ************************************* 164.1 Моторная лодка движется по реке со скоростью ************************************* 164.2 Моторная лодка движется по реке со скоростью ************************************* 164.3 Моторная лодка движется по реке со скоростью ************************************* 164.4 Моторная лодка движется по реке со скоростью ************************************* 164.5 Моторная лодка движется по реке со скоростью ************************************* 165.1 Какую работу совершают действующие на материальную точку силы, если ее кинетическая энергия уменьшается с 50 до 25Дж? D) –25; *************************************
166.2 Груз массой 166.3 Груз массой ************************************* 166.4 Груз массой 166.5 Груз массой
************************************* 167.2 На точку ************************************* 167.3 На точку ************************************* 167.4 На точку ************************************* 167.5 На точку 168.1 Коэффициент перевода мощности, выраженной в лошадиных силах, в кВт. C) 0,736; ************************************* 168.2 Коэффициент перевода мощности, выраженной в кВт, в лошадиные силы D) 1,36; *************************************
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.160.219 (0.271 с.) |
 .
. .
. .
. .
.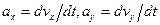 .
.
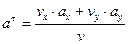 .
.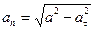 .
. .
. .
. .
. .
.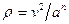 .
.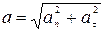 .
.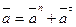 .
. .
. . Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля
. Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля 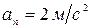 . Д)200
. Д)200 . Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля
. Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля  . Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля
. Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля  . Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля
. Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля 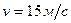 . Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля
. Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля  по дуге окружности радиуса
по дуге окружности радиуса 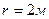 . Определить нормальное ускорение точки. Е)200
. Определить нормальное ускорение точки. Е)200 . Определить нормальное ускорение точки. Д)100
. Определить нормальное ускорение точки. Д)100 . Определить нормальное ускорение точки в момент времени, когда ее полное ускорение
. Определить нормальное ускорение точки в момент времени, когда ее полное ускорение  . C) 3;
. C) 3;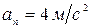 и касательное
и касательное 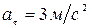 ускорения точки. Определить полное ускорение точки. D) 5;
ускорения точки. Определить полное ускорение точки. D) 5; 91.1 Объект 3, установленный на двух цилиндрических катках 1 и 2, совершает поступательное движение. Чему равно ускорение точки С, если ускорение точки А равно
91.1 Объект 3, установленный на двух цилиндрических катках 1 и 2, совершает поступательное движение. Чему равно ускорение точки С, если ускорение точки А равно 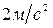 , причем
, причем 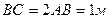 . C) 2;
. C) 2;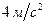 , причем
, причем  , причем
, причем  , причем
, причем  , причем
, причем 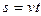 .
. .
. .
. .
. .
.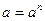 .
. .
.

 .
.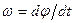 .
. .
. .
.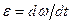 .
. .
. от оси вращения.
от оси вращения.



 рад: E) 3600.
рад: E) 3600.



 .
. . A) 0;
. A) 0; . A) 0;
. A) 0; , то вектор угловой скорости при переносном движении и вектор относительной скорости расположены под углом: A) 00;
, то вектор угловой скорости при переносном движении и вектор относительной скорости расположены под углом: A) 00; .
.
 длиной
длиной 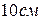 движется в плоскости чертежа. В некоторый момент времени точки А и В стержня имеют скорости
движется в плоскости чертежа. В некоторый момент времени точки А и В стержня имеют скорости 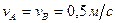 . Определить модуль мгновенной угловой скорости стержня A) 0;
. Определить модуль мгновенной угловой скорости стержня A) 0; равна
равна  . Определить скорость точки соприкосновения колеса с плоскостью. 0
. Определить скорость точки соприкосновения колеса с плоскостью. 0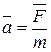 .
.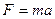 .
. .
. .
. .
. .
. .
. , где
, где  .
. .
. .
. .
. .
. .
. .
. .
.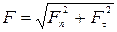 .
. .
. .
. .
. .
.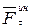 и
и 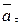 направлены
направлены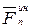 и
и 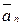 направлены
направлены .
.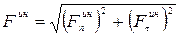 .
.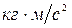 .
.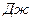 .
. .
. .
.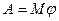 .
. .
.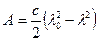 .
.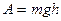 .
. , то работа этой силы C)
, то работа этой силы C)  .
. , то работа этой силы E)
, то работа этой силы E) 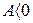 .
. , то работа этой силы C)
, то работа этой силы C)  , то работа этой силы A)
, то работа этой силы A)  .
.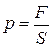 .
. и
и  .
. .
. .
.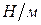 .
. .
. .
.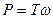 .
. .
.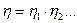 .
. .
. 162.1 На поршень гидроцилиндра действует сила
162.1 На поршень гидроцилиндра действует сила  , его скорость
, его скорость  . Определить в кВт мощность силы давления масла. E) 12.
. Определить в кВт мощность силы давления масла. E) 12.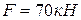 , его скорость
, его скорость  , его скорость
, его скорость 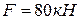 , его скорость
, его скорость 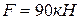 , его скорость
, его скорость  163.1 К диску диаметра
163.1 К диску диаметра 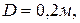 который вращается с угловой скоростью
который вращается с угловой скоростью  , прижимаются две колодки. Сила трения между диском и колодкой равна
, прижимаются две колодки. Сила трения между диском и колодкой равна  . Определить мощность силы трения. C) –800;
. Определить мощность силы трения. C) –800; который вращается с угловой скоростью
который вращается с угловой скоростью  который вращается с угловой скоростью
который вращается с угловой скоростью  который вращается с угловой скоростью
который вращается с угловой скоростью 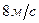 . Сила тяги двигателя равна
. Сила тяги двигателя равна  . Определить в
. Определить в  мощность силы тяги двигателя B) 24;
мощность силы тяги двигателя B) 24; . Сила тяги двигателя равна
. Сила тяги двигателя равна  . Сила тяги двигателя равна
. Сила тяги двигателя равна 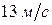 . Сила тяги двигателя равна
. Сила тяги двигателя равна 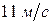 . Сила тяги двигателя равна
. Сила тяги двигателя равна 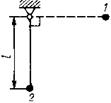 166.1 Груз массой
166.1 Груз массой  подвешен на нити длиной
подвешен на нити длиной 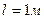 . Какую работу совершает сила тяжести груза при перемещении его в вертикальной плоскости из положения 2 в положение 1. B) –4;
. Какую работу совершает сила тяжести груза при перемещении его в вертикальной плоскости из положения 2 в положение 1. B) –4; подвешен на нити длиной
подвешен на нити длиной  подвешен на нити длиной
подвешен на нити длиной 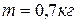 подвешен на нити длиной
подвешен на нити длиной 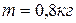 подвешен на нити длиной
подвешен на нити длиной 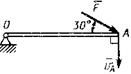 167.1 На точку
167.1 На точку 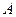 кривошипа, который вращается вокруг горизонтальной оси, действует в вертикальной плоскости сила
кривошипа, который вращается вокруг горизонтальной оси, действует в вертикальной плоскости сила  . Определить мощность силы
. Определить мощность силы 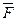 , если скорость
, если скорость  точки
точки 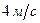 . C) 200;
. C) 200;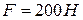 . Определить мощность силы
. Определить мощность силы  . Определить мощность силы
. Определить мощность силы  . Определить мощность силы
. Определить мощность силы  . Определить мощность силы
. Определить мощность силы 


