
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Е) Начало вектора совпадает с началом первого вектора, а конец - с концом последнего вектора.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
B) Ограничения, препятствующие перемещению объектов в пространстве ************************************* 2.1 Принцип освобождаемости от связей A) Всякий несвободный объект можно рассматривать как свободный, если отбросить связи, заменив их реакциями ************************************* 3.1 Как направлена реакция шарнирно-подвижной опоры (опора на катках)? D) перпендикулярно опорной поверхности. ************************************ 3.2 Как направлена реакция шарнирно-неподвижной опоры? В) направление неизвестно, поэтому в расчетах берем проекции реакции на координатные оси ************************************* 3.3 Как направлена реакция натянутой нити? А) вдоль нити. ************************************* 3.4 Как направлена реакция стержня? С) вдоль стержня ************************************* 3.5 Как направлена реакция угла? D) перпендикулярно опорной поверхности. ************************************* 3.6 Как направлена реакция плоскости? D) перпендикулярно опорной поверхности. ************************************* 3.7 Как направлена реакция подпятника? В) направление неизвестно, поэтому в расчетах берем проекции реакции на координатные оси. ************************************* 3.8 Как направлена реакция подшипника? Е) перпендикулярно оси подшипника. ************************************* 4.1 Как определить равнодействующую равномерно распределенной нагрузки?) Е) ************************************* 4.2 Как определить равнодействующую сил, равномерно распределенных вдоль отрезка прямой по линейному закону? В) ************************************* 5.1 На каком расстоянии от начала нагруженного участка длиной В) ************************************* 5.2 На каком расстоянии от начала нагруженного участка длиной А) посередине нагруженного участка; ************************************* 5.3 На каком расстоянии приложена от большей стороны прямоугольного треугольника равнодействующая сил, распределенных вдоль отрезка прямой по линейному закону?) С) 5.4 На каком расстоянии приложена от большей стороны прямоугольного треугольника равнодействующая сил, распределенных вдоль отрезка прямой по линейному закону? В) на одной трети нагруженного участка; 6.1 Что называют реакцией связи? D) Сила, с которой данная связь действует на объект, препятствуя его перемещениям *************************************
************************************* 7.2 Укажите в какой точке приложена реакция угла Е) D.
7.3 Укажите в какой точке приложена реакция шарнирно-неподвижной опоры А) А;
7.4 Укажите в какой точке приложена реакция опоры на катках Е) D. ************************************* 7.5 Укажите в какой точке приложена реакция нити С) С;
С) СЕ;
************************************* 7.6 Укажите в какой точке приложена реакция стержня Е) D.
************************************ 8.1 Что изучает статика? A) Раздел механики, изучающий равновесие объектов под действием приложенных к ним сил. ************************************* 9.1 Какая сила называется равнодействующей системы сил? A) Действие, которой равно действию системы в целом. ************************************* 10.1 Что такое уравновешенная система сил? A) Система, в которой все силы взаимно уравновешивают друг друга. ************************************* 10.2 Что такое уравновешивающая сила? B) Сила, приводящая систему сил к равновесию. ************************************* 10.3 Что такое абсолютно твердое тело? B) Тело, не изменяющее свою форму и размеры под действием внешних сил. ************************************* 10.4 Что такое проекция вектора на координатную ось? A) Отрезок оси, заключенный между проекциями начала и конца вектора на эту координатную ось. ************************************* 10.5 Что такое векторное величина? D) Величина, физический смысл которой определяется не только ее числовым значением, но и направлением в пространстве. ************************************* 11.1 Чему равна равнодействующая двух сил, действующих по одной прямой в одну сторону? D) Их сумме. 11. Чему равна равнодействующая двух сил, действующих по одной прямой в разные стороны? A) Их разности. ************************************* 12.1 Какая сила называется сосредоточенной? C) Сила, приложенная в точке. ************************************* 13.1 Изменяется ли действие силы на поступательно движущиеся объект при переносе силы в точку, лежащую на линии действия силы? C) Действие силы не изменится. ************************************* 14.1 Какой силовой фактор добавится при переносе силы в точку, не лежащую на линии действия силы? D) Дополнительно к поступательному воздействию силы добавится вращательное воздействие вызванное моментом силы относительно точки ее переноса. ************************************* 15.1 Когда уравновешиваются две равные по величине силы? D) Когда они действуют по одной прямой в разные стороны. ************************************* 16.1 Какие пары сил являются эквивалентными друг другу? C) Пары, моменты которых одинаковы по величине и направлению. ************************************* 17.1 Чему равен момент равнодействующей по теореме Вариньона при условии действия нескольких моментов на плоскость? D) Алгебраической сумме составляющих моментов. ************************************* 18.1 Как определяется направление равнодействующей системы сходящихся сил при построении силового многоугольника? D) Линии действия сил которых, пересекаются в одной точке. ************************************* 20.1 Каковы уравнения равновесия плоской системы сходящихся сил? А) ************************************* 20.2 Каковы уравнения равновесия пространственной системы сходящихся сил? В) ************************************* 21.1 Сколько уравнений равновесия имеет плоская система сходящихся сил? А) 2 ************************************* 21.2 Сколько уравнений равновесия имеет пространственная система сходящихся сил? В) 3; ************************************* 22.1 По какому правилу складываются геометрически две сходящиеся силы? D) По правилу параллелограмма. ************************************* 23.1 Назовите геометрическое условие равновесия плоской системы сходящихся сил? C) Силовой многоугольник должен быть замкнутым. ************************************* 24.1 Каковы уравнения равновесия плоской системы произвольно расположенных сил? С) ************************************* 24.2? Каковы уравнения равновесия пространственной системы произвольно расположенных сил? D) ************************************* 25.1 Теорема Вариньона о моменте равнодействующей плоской системы сил А) Момент равен алгебраической сумме моментов составляющих сил относительно той же точки; ************************************* 26.1 Сколько уравнений равновесия имеет система сил, произвольно расположенная на плоскости? В)3 ************************************* 26.2 Сколько уравнений равновесия имеет система сил, произвольно расположенных в пространстве? Д)6 ************************************* 27.1 Какой объект называется рычагом? А) Объект, имеющий неподвижную ось вращения и находящийся под действием сил, лежащих в плоскости, перпендикулярной к этой оси. ************************************* 28.1 Какое условие выполняется, когда рычаг находится в покое? Е) ************************************* 29.1 система сил называется парой сил? D) параллельно паре сил, но в разных направлениях. ************************************* 33.1 Изменяется ли момент силы относительно данной точки при переносе силы вдоль линии ее действия? В) нет. ************************************* 34.1 Каком случае момент силы относительно данной точки равен нулю? А) Момент равен алгебраической сумме моментов составляющих сил относительно той же точки. ************************************* 36.1 Что называют коэффициентом устойчивости? А) ************************************* 36.2 Что называют коэффициентом устойчивости? А) отношение удерживающего момента к опрокидывающему; 37.1 Сколько уравнений равновесия имеет система параллельных сил, расположенных на плоскости. А)2 ************************************* 38.1 Что такое момент силы относительно точки? B) Произведение модуля силы на расстояние от линии ее действия до точки. ************************************* 39.1 что такое момент пары сил? A) Произведение модуля одной из сил пары на расстояние между линиями действия сил пары. *************************************
************************************* 40.2 В одной плоскости расположены три пары сил. Определить момент равнодействующий по теореме Вариньона, если моменты ************************************* 40.3 (В одной плоскости расположены три пары сил. Определить момент равнодействующий по теореме Вариньона, если моменты ************************************* 40.4 В одной плоскости расположены три пары сил. Определить момент равнодействующий по теореме Вариньона, если моменты ************************************* 40.5 В одной плоскости расположены три пары сил. Определить момент равнодействующий по теореме Вариньона, если моменты *************************************
************************************* 41.2 Консольная балка нагружена парами сил с моментами ************************************* 41.3 Консольная балка нагружена парами сил с моментами ************************************* 41.4 Консольная балка нагружена парами сил с моментами ************************************* 41.5 Консольная балка нагружена парами сил с моментами *************************************
************************************* 42.2 На брус ************************************* 42.3 На брус ************************************* 42.4 На брус ************************************* 42.5 На брус ************************************* 43.1 Чему равна по модулю равнодействующая двух параллельных сил, направленных в одну сторону? D) Сумме составляющих сил. ************************************* 43.2 Чему равна по модулю равнодействующая двух параллельных сил, направленных в разные стороны? A) разности составляющих сил. ************************************* 43.3 Чему равна равнодействующая пары сил? Е) 0. ************************************* 44.1 Что такое центр тяжести материального объекта? A) Точка приложения силы веса ************************************* 45.1 Назовите формулы для определения центра тяжести сложного плоского сечения. A) ************************************* 46.1 Где находится центр тяжести прямоугольника? C) В точке пересечения диагоналей. ************************************* 46.2 Где находится центр тяжести треугольника? C) В точке пересечения медиан). ************************************* 46.3 Где находится центр тяжести треугольника? C) На одной трети высоты; ************************************* 46.4 Где находится центр тяжести окружности? A) На пересечении осей; ************************************ 46.5 Где находится центр тяжести у тела вращения? D) на оси вращения; ************************************* 47.1 Если фигура имеет одну ось симметрии, то центр тяжести находится A) На оси симметрии; ************************************* 47.2 Если фигура имеет две оси симметрии, то центр тяжести находится A) На пересечении осей; ************************************* 48.1 Площадь прямоугольника A) ************************************* 48.2 Площадь треугольника B) ************************************* 48.3 Площадь круга D) ************************************* 49.1 Что называется центром параллельных сил? D) Точка приложения равнодействующей системы параллельных сил. ************************************* 50.1 Что такое ферма? A) стержневая система, каждый стержень которой при действии поперечных сил работает преимущественно на растяжение или сжатие. ************************************* 51.1 Условие статической определимости плоских ферм B) ************************************* 52.1 Нулевые стержни определяем: E) По леммам о нулевых стержнях. ************************************* 53.1 Коэффициент трения качения это: C) Расстояние, на которое смещена результирующая реакция опорной поверхности упругого колеса от вертикальной оси колеса; ************************************* 54.1 Коэффициент трения качения это: A) ************************************* 55.1 Сила трения направлена: B) В сторону противоположную движению объекта. ************************************* 55.2 Сила трения возникает между: D) Трущимися поверхностями; ************************************* 56.1 чему равен коэффициент трения скольжения? B) Отношению силы трения к силе нормального давления. ************************************* 56.2 Чему равен коэффициент трения скольжения идеальной поверхности? B) 0; ************************************* 57.1 Реакция плоскости измеряется C) Н; ************************************* 57.2 Реакция угла измеряется C) Н; ************************************* 57.3 Реакция нити измеряется C) Н; ************************************* 57.4 Реакция стержня измеряется C) Н; ************************************* 57.5 Реакция подпятника измеряется C) Н; ************************************* 57.6 Реакция подшипника измеряется C) Н; ************************************* 57.7 Реакция шарнира измеряется C) Н; ************************************* 57.8 Реакция подвижной опоры измеряется C) Н; ************************************* 57.9 Реакция неподвижной опоры измеряется C) Н; ************************************* 57.10 Реакция поверхности измеряется C) Н; *********************************
B) 5;
************************************* 58.2 Какой стержень не нагружен?
************************************* 58.3 Какой стержень не нагружен?
59.1 1 кН это: A) 103 Н; 59.2 1Н это: A) *************************************
60.2 Определить в ************************************* 60.3 Определить в ************************************* 60.4 Определить в ************************************* 60.5 Определить в ************************************* 60.6 Определить в ************************************* 60.7 Определить в ************************************* 60.8 Определить в ************************************* 61.1 Что изучает кинематика? C) Раздел механики, изучающий движение объектов, без учета их масс и сил, вызывающих это движение ************************************* 62.1 Что такое траектория движения материальной точки? C) Линия, по которой движется материальная точка. ************************************* 62.2 Что такое механическое движение? D) Изменение положения тела в пространстве по отношению к принятой системе отсчета. ************************************* 63.1 Уравнение прямой B) ************************************* 63.2 Уравнение параболы A) ************************************* 63.3 Уравнение эллипса D) ************************************* 65.1 Как по уравнениям движения точки в координатной форме определить ее траекторию? А) исключить параметр ************************************* 66.1 Какие Вы знаете способы задания движения материальной точки? D) Геометрический (или естественный) и координатный. ************************************* 67.1 Что такое скорость? А) путь, пройденный за единицу времени. ************************************* 68.1 Как направлен вектор скорости? B) По радиусу к центру кривизны. ************************************* 95.1 Закон движения при неравномерном движении точки. В) ************************************* 95.2 Закон движения при равномерном движении точки. Е) ************************************* 95.3 Закон движения при равнопеременном движении точки? С) ************************************* 96.1 Чему равна скорость при неравноменном движении? В) ************************************* 96.2 Чему равна скорость при равноменном движении? С) 96.3 Чему равна скорость при равнопеременном движении? Е) ************************************* 97.1 Чему равно ускорение при неравномерном движении С) ************************************* 97.2 Чему равно ускорение при равномерном движении А) ************************************* 97.3 Чему равно ускорение при равнопеременном движении С) ************************************* 97.4 Чему равно касательное ускорение при равномерном движении В) 0. ************************************* 97.5 Чему равно нормальное ускорение при равномерном движении А) ************************************* 97.6 Чему равно ускорение при прямолинейном равномерном движении Е) 0. ************************************* 98.1 Единица измерения линейного перемещения. C) м; ************************************* 98.2 Единица измерения линейной скорости. D) м/с; ************************************* 98.3 Единица измерения линейного ускорения. E) м/с2. ************************************* 98.4 Единица измерения касательного ускорения. E) м/с2. ************************************* 98.5 Единица измерения нормального ускорения. E) м/с2. ************************************* 99.1 Формула перевода углового перемещения в радианах в количество оборотов С) ************************************* 100.1 Закон вращательного движения при неравномерном вращении объекта А) ************************************* 100.2 Закон вращательного движения при равномерном движении объекта D) ************************************* 100.3 Закон вращательного движения при равнопеременном движении объекта С) ************************************* 101.1 Угловая скорость при неравномерном вращении объекта. С) ************************************* 101.2 Угловая скорость при равномерном вращении объекта. С) ************************************* 101.3 Угловая скорость при равнопеременном вращении объекта. D) ************************************* 102.1 Угловое ускорение при неравномерном вращении объекта. D) ************************************* 102.2 Угловое ускорение при равномерном вращении объекта. A) 0. ************************************* 102.3 Угловое ускорение при равнопеременном вращении объекта. B) ************************************* 103.1 Касательное ускорение точки при равномерном вращении объекта. A) 0. 104.1 Полное ускорение точки при равномерном вращении объекта. A) 0. ************************************* 104.2 Полное ускорение при равнопеременном вращении объекта. C) ************************************* 105.1 Зависимость линейной скорости точки от угловой скорости вращения объекта вокруг неподвижной оси, при расположении точки на расстоянии Е) ************************************* 106.1 Как направлены векторы угловой скорости и углового ускорения С) вдоль оси вращения ************************************* 107.1 Формула перевода угловой скорости рад/сек в об/мин. В) ************************************* 108.1 Зависимость касательного ускорения точки от углового ускорения при вращении объекта вокруг неподвижной оси. В) ************************************* 108.2 Зависимость нормального ускорения точки от угловой скорости при вращении объекта вокруг неподвижной оси. D) ************************************* 109.1 Что такое угловая скорость? B) Угол поворота объекта за единицу времени. ************************************* 109.2 Что такое угловое ускорение? C) Изменение угловой скорости за единицу времени. ************************************* 110.1 Единица измерения углового перемещения. A) рад; ************************************* 110.2 Единицы измерения угловой скорости. D) рад/с; ************************************* 110.3 Единицы измерения углового ускорения E) рад/с2. ************************************* 111.1 3600 это: B) 1 оборот; ************************************* 111.2 ************************************* 111.3 1 оборот колеса это: B) ************************************* 112.1 Основная теорема кинематики В) ************************************* 113.1 Как определить абсолютную скорость при сложном движении точки. С) 113.2 Как определить абсолютное ускорение при сложном движении точки. В) ************************************* 113.3 Как определить кориолисово ускорение при сложном движении точки Е) ************************************* 113.4 Как определить кориолисово ускорение при сложном движении точки. Е) ************************************* 114.1 Единица измерения Кориолисова ускорения. E) м/с2. ************************************* 115.1 Чему равно кориолисово ускорение точки при поступательном переносном движении ************************************* 115.2 Чему равно кориолисово ускорение закрепленной точки на объекте при вращении объекта ************************************* 116.1 Если вектор угловой скорости при переносном движении параллелен вектору относительной скорости, то Кориолисово ускорение равно: A) 0; ************************************* 116.2 Если вектор угловой скорости при переносном движении параллелен вектору относительной скорости, то угол между векторами равен: A) 00; ************************************* 117.1 Если угол между векторами переносной угловой скорости и относительной скорости равен 00, то A) векторы параллельны; ************************************* 117.2 Если ************************************* 118.1 (Кориолисово ускорение равно нулю, если A) ************************************* 118.2 Кориолисово ускорение равно нулю, если A) ************************************* 118.3 Кориолисово ускорение равно нулю, если синус угла между векторами переносной угловой скорости и относительной скорости равен: A) ************************************* 119.1 Что такое мгновенный центр скоростей? A) Точка пространства, в которой в данный момент времени скорость как минимум двух точек объекта равны нулю. ************************************* 120.1 Если известны направления векторов скоростей двух точек, то мгновенный центр скоростей находится: B) На пересечении перпендикуляров к этим векторам; *************************************
121.1 Стержень ************************************* 122.1 Скорость центра катящегося по плоскости колеса радиуса 123.1 где находится мгновенный центр скоростей катящегося колеса по горизонтальной плоскости? B) В точке касания колеса с плоскостью. ************************************* 124.1 Основной закон динамики С) ************************************* 125.1 Уравнение движения объекта, движущегося поступательно Е) ************************************* 126.1 Уравнение движения объекта, вращающегося вокруг неподвижной оси А) ************************************* 127.1 Основное уравнение динамики: C) ************************************* 127.2 Основное уравнение динамики в проекциях на координатные оси D) ************************************* 127.3 Основное уравнение динамики в проекциях на естественные оси. E) ************************************* 127.4 Основное уравнение динамики в дифференциальной форме в проекциях на координатные оси. B) ************************************* 128.1 Что является движущим фактором, при поступательном движении объекта? B) Сила. ************************************* 128.2 Что является движущим фактором, при вращении объекта вокруг неподвижной оси? C) Скорость. ************************************* 129.1 Каков физический смысл понятия масса материального объекта? C) Это мера инертности объекта, характеризующая его способность воспринимать ускорение под действием приложенной к нему внешней силы. ************************************* 130.1 Укажите формулу теоремы о движении центра масс. A) ************************************* 131.1 Нормальная составляющей силы A) ************************************* 131.2 Нормальная составляющей силы A) ************************************* 131.3 Нормальная составляющей силы A) ************************************* 132.1 Касательная составляющей силы B) ************************************* 132.2 Касательная составляющей силы B) ************************************* 132.3 Касательная составляющей силы B) ************************************* 133.1 Сила в проекциях на координатные оси. C) ************************************* 133.2 Сила в проекциях на естественные оси. D) ************************************* 133.3 Сила в векторной форме E) ************************************* 134.1 Крутящий момент A) ************************************* 135.1 Единицы измерения крутящегося момента D) ************************************* 136.1 Метод кинетостатики в математическом выражении. A) ************************************* 137.1 Силы инерции возникает: B) При движении объекта с ускор |
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.122 (0.022 с.) |

 .
. ;
;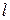 приложена равнодействующая равномерно распределенной нагрузки?
приложена равнодействующая равномерно распределенной нагрузки? ;
; ;
; 7.1 Укажите в какой точке приложена реакция жесткой заделки А) А;
7.1 Укажите в какой точке приложена реакция жесткой заделки А) А;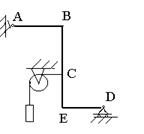 *************************************
************************************* 7.7 Укажите на каком участке приложена равномерно распределенная нагрузка
7.7 Укажите на каком участке приложена равномерно распределенная нагрузка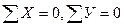 ;
; ;
; ;
; ;
; .
. ;
; 40.1 В одной плоскости расположены три пары сил. Определить момент равнодействующий по теореме Вариньона, если моменты
40.1 В одной плоскости расположены три пары сил. Определить момент равнодействующий по теореме Вариньона, если моменты 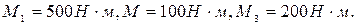 B) –200;
B) –200;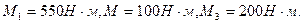 A) –250;
A) –250; C) 200;
C) 200; D) –300;
D) –300; E) -400.
E) -400. 41.1 Консольная балка нагружена парами сил с моментами
41.1 Консольная балка нагружена парами сил с моментами  и
и 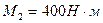 . Определить момент в заделке по теореме Вариньона. A) 200;
. Определить момент в заделке по теореме Вариньона. A) 200;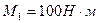 и
и  . Определить момент в заделке по теореме Вариньона. E) –100.
. Определить момент в заделке по теореме Вариньона. E) –100.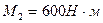 . Определить момент в заделке по теореме Вариньона. D) 400;
. Определить момент в заделке по теореме Вариньона. D) 400; и
и  42.1 На брус
42.1 На брус  , закрепленный в шарнире
, закрепленный в шарнире 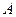 , действуют вертикальные силы
, действуют вертикальные силы  и
и  . Определить расстояние
. Определить расстояние  , необходимое для того, чтобы брус в положении равновесия был горизонтальным, если расстояние
, необходимое для того, чтобы брус в положении равновесия был горизонтальным, если расстояние  . D) 6;
. D) 6; . C) 12;
. C) 12; . E) 18.
. E) 18. A) 9;
A) 9; . B) 3;
. B) 3;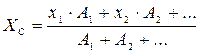 ;
;  ;
; ;
; ;
; ;
; ;
; ;
; 58.1 Какой стержень не нагружен?
58.1 Какой стержень не нагружен? D) 7;
D) 7;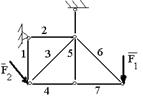 B) 5;
B) 5; ;
; 60.1 Определить в
60.1 Определить в  момент в заделке А консольной балки, если сила натяжения троса
момент в заделке А консольной балки, если сила натяжения троса  и расстояние
и расстояние  .) 25
.) 25 и расстояние
и расстояние  и расстояние
и расстояние  и расстояние
и расстояние  и расстояние
и расстояние  и расстояние
и расстояние  и расстояние
и расстояние  и расстояние
и расстояние  .
. .
. .
. .
. .
.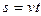 .
. .
. .
. .
. .
.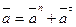 .
.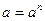 .
. .
. .
.

 .
. .
.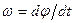 .
. .
. .
.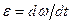 .
. .
. от оси вращения.
от оси вращения.



 рад: E) 3600.
рад: E) 3600.



 .
. . A) 0;
. A) 0; . A) 0;
. A) 0; , то вектор угловой скорости при переносном движении и вектор относительной скорости расположены под углом: A) 00;
, то вектор угловой скорости при переносном движении и вектор относительной скорости расположены под углом: A) 00; .
.
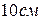 движется в плоскости чертежа. В некоторый момент времени точки А и В стержня имеют скорости
движется в плоскости чертежа. В некоторый момент времени точки А и В стержня имеют скорости 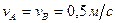 . Определить модуль мгновенной угловой скорости стержня A) 0;
. Определить модуль мгновенной угловой скорости стержня A) 0; равна
равна  . Определить скорость точки соприкосновения колеса с плоскостью. 0
. Определить скорость точки соприкосновения колеса с плоскостью. 0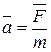 .
.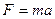 .
. .
. .
. .
. .
. .
. , где
, где  .
. .
. .
. .
. .
. .
. .
. .
.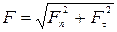 .
. .
. .
. .
. .
.


