Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.Содержание книги
Поиск на нашем сайте
Геометрические векторы. Рассмотри на плоскости 2 точки А и Б. По соединяющему их от резку можно двигаться в обе стороны. Если А – начало, а Б – конец, получим направленный отрезок АБ, иначе БА. Определение – геометрический вектор – направленный отрезок который можно перемещать параллельно самому себе. Если у вектора совпадает начало и конец, то вектор 0й. Длинной вектора вектора будем называть величину соответствующей направлению отрезка или расстояния между нач. и конечными точками вектора и обозначается – модуль(AB). Если длинна вектора равна 1му, то вектор-единичный. 2 вектора равны, если они лежат на одной или на параллельных прямых, направленных в одну сторону и их длинны равны. 1й вектор имеющий одинаковое направление с векротом АБ – орт вектора АБ. Орт = (вектор АБ/длину вектора). Угол между векторами А и Б – угол С причем 0<C<
Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов. Скалярное произведение векторов – число которое находится по формуле |a|*|b|* cos(c), с – угол между векторами. Скалярное произведение (А,Б)=|а|*пр.а Б. = |Б|* пр.б. А. Свойства скалярного произведения: 1) (а,б)=(б,а) тк cos(-c) = cos(c); 2) (а,б+с)= (а,б)+(а,с) 3) (α*а,б)=(а, α*б)= α(а,б) 4) (а,а)=|a|*|a| * cos(0) = |a|^2 5) Скалярное произведение |a|*|a|=0 только тогда, когда вектор а =0 6) Для того чтобы векторы а и б были ортогональны достаточно, чтобы их векторное произведение равнялось 0. Скалярное произведение векторов в координатной форме А{x1,y1,z1} B{x2,y2,z2} (a,b)= x1x2+y1y2+z1z2 Док-во: рассмотрим 2 вектора в базисе ijk. А=x1i+y1j+z1k, b=x2i+y2j+z2k (А,B) = (x1i+y1j+z1k, x2i+y2j+z2k)=x1x2(I,j) + x1y1(I,j)+x1z2(I,k)+y1x2(j,i)+y1y2(j,j)+y1z2(j,k)+z1x2(k,i)+z1y2(k,j)+z1z2(k1,k2) т.к i,j,k попарно ортогональны векторное произведение I,j,k = 0, а векторное произведение ijk вектора самого на себя = 1 получаем (а,б)=x1x2+y1y2+z1z2 Векторное произведение векторов. В векторном произведении [a,b]=с Такой что 1) |c|=|a|*|b|*sin( Свойства векторного произведения: 1) [a,b]=-[b,a] 2) [a,b+c]=[a,b]+[a,c] 3) [a+b,c]=[a,c]+[b,c] 4) [
5) [a,a]=0 Необходимость и достаточность условия коллинеарности векторов для того, чтобы а||б необходимо и достаточно, чтобы векторное произведение было равно 0. А||B если их координаты пропорциональны Геометрический смысл векторного произведения. |[a,b]|= площади параллелограмма, построенного на векторах а и б. Векторное произведение в координатной форме. А={x1,y1,z1} b={x2,y2,z2} [a,b]= I*| Доказательство теоремы. Предположим противное: векторы Определение. Система Определение. Базис пространства Rn называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину. В пространстве Rn в естественном скалярном произведении
Билет №11 Билет №12 Билет №13 Свойства решений линейной системы. Нейтральная совместность единой системы. Совместность единой системы. Если вектор x является решением однородной системы A·x = 0, то вектор α x также является решением этой системы. Здесь α — произвольное число. Если векторы x и y являются решениями однородной системы A·x = 0, то вектор x + y также является решением этой системы. Если вектор x является решением однородной системы A·x = 0, а вектор и y — решение неоднородной системы A·x = b, то вектор x + y является решением неоднородной системы A·x = b. Если векторы x и y являются решениями неоднородной системы A·x = b, то вектор x − y является решением однородной системы A·x = 0. Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn. Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу матрицы системы. Это утверждение называют теоремой Кронекера-Капелли. Система линейных алгебраических уравнений
очевидно несовместна. Ранги расширенной матрицы системы матрицы системы не равны, rank Ap = 2, rank A = 1, rank Ap ≠ rank A:
Билет №14 Билет №15 Билет №16 Линейный оператор в Линейные операторы. Матрица линейного оператора. Примеры линейных операторов. Определение. Если каждому элементу Результат действия оператора A на элемент Если элементы Множество элементов пространства Rn, для которых определено действие оператора A, называют областью определения оператора A и обозначают D ( A). Множество элементов пространства Rn, которые являются образами элементов из области определения D ( A) оператора A, называют образом оператора A и обозначают Im(A). Если Ядром оператора называется множество элементов пространства Rn, образом которых является нуле нулевой элемент. Ядро оператора обозначают Ker(A):
Определение. Оператор A, действующий в пространстве Rn называется линейным оператором, если для любых
Определение. Матрица, столбцами которой являются координаты образов соответствующих базисных векторов некоторого базиса в Rn —
называется матрицей линейного оператора Билет №17 Действия с линейными операторами и их матрицами
Рассмотрим линейный оператор Ядром линейного оператора называется множество элементов из Для линейного оператора, действующего в n-мерном линейном пространстве сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор: ранг оператора равен рангу его матрицы; ядро оператора совпадает с множеством решений линейной однородной системы с матрицей столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора. Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
Билет №18 Преобразование координат вектора и матрицы линейного оператора. Их свойства и вычисления. Пусть в
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса
Эта матрица называется матрицей перехода от старого базиса к новому. Изменение матрицы линейного преобразования при изменении базиса В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой. Пусть Предложение 19.1 Пусть
Доказательство. Пусть Определение 19.2 Две квадратных матрицы Следствие 19.1 Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.
Билет №19. Собственные значения и собственные векторы линейного оператора. Их свойства и вычисление. Определение. Пусть A — линейный оператор, действующий в линейном пространстве Rn. Число По теореме о связи координат образа и прообраза имеем: Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы
Легко видеть, что определитель Определение. Уравнение Примеры. 1. Нулевой оператор Свойства собственных векторов Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения: 1) характеристический многочлен оператора, действующего в Rn является многочленом n -й степени относительно 2) линейный оператор, действующий в Rn, имеет не более n различных собственных значений; 3) собственные векторы оператора определяются с точностью до постоянного сомножителя; поэтому принять вычислять собственные векторы единичной длины — орты собственных векторов; докажем, что если 4) корни характеристического многочлена не зависят от базиса; 5) собственные векторы, отвечающие различным собственным значениям, линейно независимы.
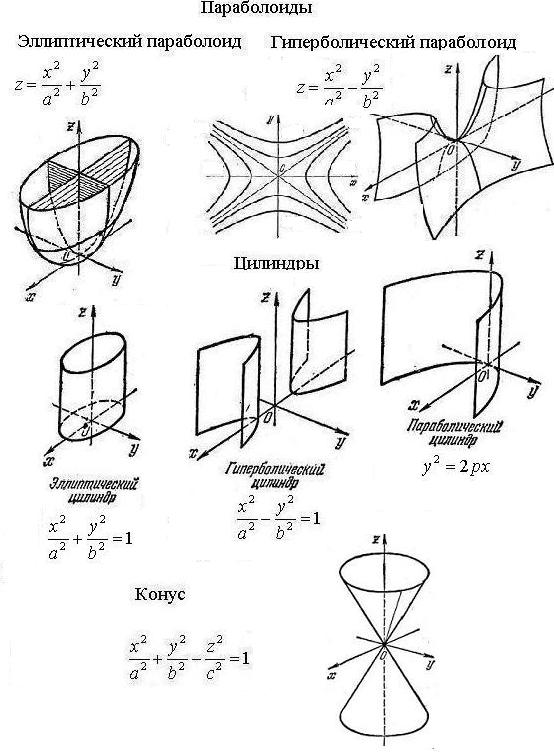
Поверхности 2-го порядка
Геометрические векторы. Рассмотри на плоскости 2 точки А и Б. По соединяющему их от резку можно двигаться в обе стороны. Если А – начало, а Б – конец, получим направленный отрезок АБ, иначе БА. Определение – геометрический вектор – направленный отрезок который можно перемещать параллельно самому себе. Если у вектора совпадает начало и конец, то вектор 0й. Длинной вектора вектора будем называть величину соответствующей направлению отрезка или расстояния между нач. и конечными точками вектора и обозначается – модуль(AB). Если длинна вектора равна 1му, то вектор-единичный. 2 вектора равны, если они лежат на одной или на параллельных прямых, направленных в одну сторону и их длинны равны. 1й вектор имеющий одинаковое направление с векротом АБ – орт вектора АБ. Орт = (вектор АБ/длину вектора). Угол между векторами А и Б – угол С причем 0<C<
Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов. Скалярное произведение векторов – число которое находится по формуле |a|*|b|* cos(c), с – угол между векторами. Скалярное произведение (А,Б)=|а|*пр.а Б. = |Б|* пр.б. А. Свойства скалярного произведения:
1) (а,б)=(б,а) тк cos(-c) = cos(c); 2) (а,б+с)= (а,б)+(а,с) 3) (α*а,б)=(а, α*б)= α(а,б) 4) (а,а)=|a|*|a| * cos(0) = |a|^2 5) Скалярное произведение |a|*|a|=0 только тогда, когда вектор а =0 6) Для того чтобы векторы а и б были ортогональны достаточно, чтобы их векторное произведение равнялось 0. Скалярное произведение векторов в координатной форме А{x1,y1,z1} B{x2,y2,z2} (a,b)= x1x2+y1y2+z1z2 Док-во: рассмотрим 2 вектора в базисе ijk. А=x1i+y1j+z1k, b=x2i+y2j+z2k (А,B) = (x1i+y1j+z1k, x2i+y2j+z2k)=x1x2(I,j) + x1y1(I,j)+x1z2(I,k)+y1x2(j,i)+y1y2(j,j)+y1z2(j,k)+z1x2(k,i)+z1y2(k,j)+z1z2(k1,k2) т.к i,j,k попарно ортогональны векторное произведение I,j,k = 0, а векторное произведение ijk вектора самого на себя = 1 получаем (а,б)=x1x2+y1y2+z1z2 Векторное произведение векторов. В векторном произведении [a,b]=с Такой что 1) |c|=|a|*|b|*sin( Свойства векторного произведения: 1) [a,b]=-[b,a] 2) [a,b+c]=[a,b]+[a,c] 3) [a+b,c]=[a,c]+[b,c] 4) [ 5) [a,a]=0 Необходимость и достаточность условия коллинеарности векторов для того, чтобы а||б необходимо и достаточно, чтобы векторное произведение было равно 0. А||B если их координаты пропорциональны Геометрический смысл векторного произведения. |[a,b]|= площади параллелограмма, построенного на векторах а и б. Векторное произведение в координатной форме. А={x1,y1,z1} b={x2,y2,z2} [a,b]= I*|
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.142.64 (0.009 с.) |

 , при условии что А и Б имеют общее начало.
, при условии что А и Б имеют общее начало. ), 2) вектор с ортогонален плоскости в которой лежат вектора а и б. 3) вектора а,б,с расположены таким образом, что из конца вектора с кратчайший поворот от вектора а к б виден против часовой стрелки.(правая тройка векторов)
), 2) вектор с ортогонален плоскости в которой лежат вектора а и б. 3) вектора а,б,с расположены таким образом, что из конца вектора с кратчайший поворот от вектора а к б виден против часовой стрелки.(правая тройка векторов) ]= α[a,b]
]= α[a,b] .
. = определитель 3-го порядка вычисл. По формуле:
= определитель 3-го порядка вычисл. По формуле: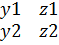 | - J*|
| - J*| 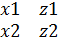 | + K*|
| + K*| 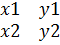 | Получаем определители 2-го порядка, которые вычисляются по формуле (y1*z2-z1*y2) получаем [a,b]={x3,y3,z3}
| Получаем определители 2-го порядка, которые вычисляются по формуле (y1*z2-z1*y2) получаем [a,b]={x3,y3,z3} попарно ортогональны, но они линейно зависимы. Тогда один из векторов линейно выражается через остальные. Например, пусть это первый вектор:
попарно ортогональны, но они линейно зависимы. Тогда один из векторов линейно выражается через остальные. Например, пусть это первый вектор:  ,
,  (ясно, что речь идет о ненулевых векторах). Тогда
(ясно, что речь идет о ненулевых векторах). Тогда  , для всех j = 2, 3, …, k, т.е.
, для всех j = 2, 3, …, k, т.е. 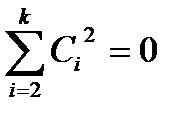 . Полученное противоречие доказывает теорему.
. Полученное противоречие доказывает теорему.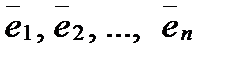 векторов из пространства Rn называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину.
векторов из пространства Rn называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину. естественный базис — ортонормированный базис.
естественный базис — ортонормированный базис.

 (В линейном пространстве). Матрица линейного пространства
(В линейном пространстве). Матрица линейного пространства ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  , то говорят, что в пространстве Rn задан оператор, действующий в пространстве Rn.
, то говорят, что в пространстве Rn задан оператор, действующий в пространстве Rn. обозначают
обозначают  .
.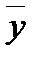 связаны соотношением
связаны соотношением  , то
, то  , то
, то 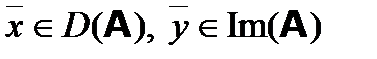 .
.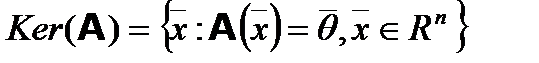 .
.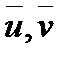 из Rn и для любого числа α справедливо:
из Rn и для любого числа α справедливо: и
и  .
.
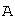 , действующий в конечномерном линейном пространстве
, действующий в конечномерном линейном пространстве 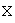 . Доказано, что образ
. Доказано, что образ  линейного оператора
линейного оператора 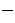 линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается
линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается  .
. :
: 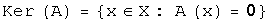 . Ядро линейного оператора
. Ядро линейного оператора 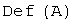 :
: 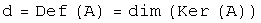 .
.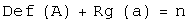 ;
;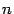 -мерном линейном пространстве
-мерном линейном пространстве  выбран базис
выбран базис 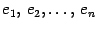 , который мы будем для удобства называть "старый" и другой базис
, который мы будем для удобства называть "старый" и другой базис  , который мы будем называть "новый". Возьмем призвольный вектор
, который мы будем называть "новый". Возьмем призвольный вектор 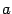 из
из 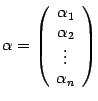 , а в новом --
, а в новом --  . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису
. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

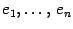 и
и 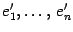 -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть
-- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть 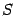 -- матрица перехода 19.1.4 а от старого базиса к новому.
-- матрица перехода 19.1.4 а от старого базиса к новому.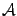 -- линейное преобразование пространства
-- линейное преобразование пространства 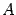 и
и  -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
-- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
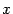 -- произвольный вектор пространства
-- произвольный вектор пространства  -- его образ, то есть
-- его образ, то есть 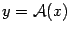 . Пусть
. Пусть 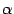 и
и 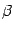 -- координатные столбцы векторов
-- координатные столбцы векторов 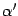 ,
, 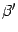 -- в новом. Тогда в силу формулы (19.3)
-- в новом. Тогда в силу формулы (19.3) 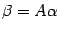 . По предложению 18.5 имеем
. По предложению 18.5 имеем 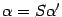 ,
,  . Подставим эти выражения в предыдущую формулу, получаем
. Подставим эти выражения в предыдущую формулу, получаем  . Откуда
. Откуда 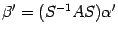 . С другой стороны, в силу формулы (19.3) в новом базисе
. С другой стороны, в силу формулы (19.3) в новом базисе 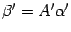 . Сравнивая это равенство с предыдущим, получаем
. Сравнивая это равенство с предыдущим, получаем 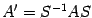 .
. и
и 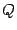 одного порядка называются подобными, если существует такая невырожденная матрица
одного порядка называются подобными, если существует такая невырожденная матрица 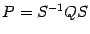 .
. называется собственным значением, а ненулевой вектор
называется собственным значением, а ненулевой вектор  из Rn — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением.
из Rn — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением.  .
.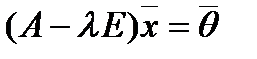 , где E — единичная матрица, а
, где E — единичная матрица, а 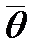 — нулевой вектор Rn.
— нулевой вектор Rn.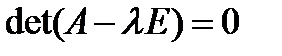 . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения
. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения  , а собственные векторы — как решения соответствующих однородных систем.
, а собственные векторы — как решения соответствующих однородных систем.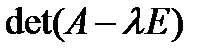 — многочлен n- й степени относительно
— многочлен n- й степени относительно  :
: 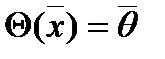 , матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е.
, матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е. 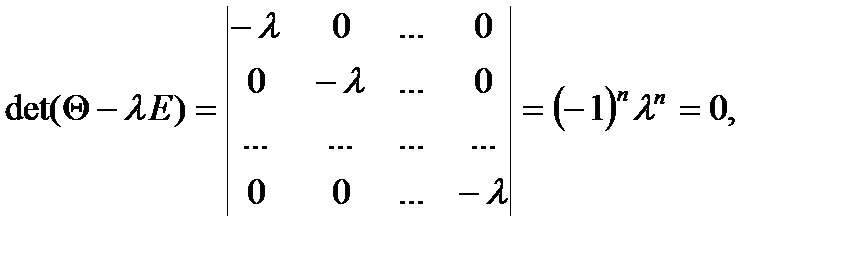 т.е.
т.е. 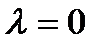 — единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
— единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn. — собственный вектор линейного оператора A, отвечающий собственному значению
— собственный вектор линейного оператора A, отвечающий собственному значению 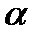 вектор
вектор 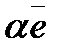 (
( )— собственный вектор оператора A, отвечающий собственному значению
)— собственный вектор оператора A, отвечающий собственному значению  ;
;