
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешенные произведения векторовСодержание книги
Поиск на нашем сайте
Смешенным произведением векторов называется число равное векторному произведению 2х векторов [a,b] скалярно умноженные на вектор c ([a,b],c) Условие компланарности 3х векторов(лежат в одной плоскости) их смешенное произведение равно 0.Геометрический смысл смеш. Произв. – объем параллелепипеда построенного на векторах a,b,c численно равен их смешенному произведению. Смешенное произведение в координатной форме. ([a,b],c)= |
3. Плоскость и прямая в пространстве. Основные задачи о прямых и плоскостях. Уравнение плоскости α проходящую через точку Мо перпендикулярн. Вектору Полученное уравнение является (ММо,n) n-нормальный вектор перпендик к плоскости α. Преобразуем уравнение A(x-x0)+B(y-y0)+c(z-z0)=Ax-Axo+By-Byo+Cz-Czo=0 D=-Axo-Byo-Czo – число Ax+By+Cz+D=0(общее уравнение плоскости) Угол между плоскостями α: A1x+B1y+C1z+D1=0 n1={A1,B1,C1} β: A2x+B2y+C2z+D2=0 n2={A2,B2,C2} Из скалярного произведения векторов φ=arcos( Уравнение плоскости, проходящую через 3 данные точки. М1(x1,y1,z1); M2(x2,y2,z2); M3(x3,y3,z3) Тогда произведение точка пространства с координатами x,y,z будет принадлежать плоскости когда M1M, M1M3, M1M2 будут компланарны, а значит их смешенное произведение будет равно 0. (M1M,[M1M3,M1M2])=0 M1M{x-x1;y-y1;z-z1} M1M2{x2-x1;y2-y1;z2-z1} M1M3{x3-x1;y3-y1;z3-z1} α: | Уравнение плоскости в отрезках. Рассмотрим общее уравнение плоскости α, которое не проходит через начало координат, при этом D≠0 α: Ax+By+Cz= ‑D|÷ (‑D) a=(-D/A), b=(-D/B), c=(-D/c) Уравнение плоскости проходящее через начало координат. D=0 Ax+Bx+Cx=0 Ax+By+D=0 –уравнение плоскости || OZ N{0,0,1}, Ax+Cz+D=0 - || OY By+Cz+D=0 ||OX Ax+D=0 ||YOZ Пример: найти расстояние от Мо {x,y,z} до плоскости α проходящей через точки М1{x1,y1,z1},М2{x2,y2,z2},М3{x3,y3,z3}. Для этого необходимо найти нормальный вектор n плоскости α, расстояние от Мо до α будет равен проекции ММо на n, т.е |MMo|*cos(β) β- угол между n и MMo. N=[M1M2,M1M3] (n,MMo)=|n|*|MMo|*cos(β).
Линия в пространстве – как частный случай – линия пересечения 2х плоскостей. Для решения щадач неудобно использовать общее уравнение прямой Каноническое уравнение прямой: n1={A1,B1,C1} ǂǂ n2={A2,B2,C2}. Рассмотрим прямую D которая проходит через точку Мо{Xo,Yo,Zo}, которая принадлежит прямой D. A{l,m,n}-направляющий вектор прямой D. Тогда произвольная точка пространства M{x,y,z} будет принадлежать прямой D только тогда когда MoM||a. MoM{x-xo;y-yo;z-zo}, если их координаты пропорциональны и D= Параметрическое уравнение прямой:
x=lt+xo y=yo+mt z=zo+nt ‑‑‑‑‑‑ параметрическое ур-е прямой. Пример: составить каноническое уравнение прямой проходящ через 2 точки М1(x1,y1,z1) M2(x2,y2,z2),берем любую из точек, лежащую на прямой к примеру М1, а за направляющий вектор возьмем вектор М1М2. Получим
Y=ty2-ty1+y1, z=tz2-tz1+z1 Общее уравнение прямой: D-линия пересечения бесконечного множества плоскостей в том числе и следующих 2х. (x-x1)/(x2-x1)=(y-y1)/(y2-y1) (x-x1)/(x2-x1)=(z-z1)/(z2-z1) Подставив числа получим неполное уравнение плоскости. Одна или даже 2 координаты направляющего вектора прямой могут равняться 0, т.е. в каноническом уравнении в знаменателе может стоять 0, и это будет не деление на 0, а отношением к 0. Составление канонического уравнения прямой как пересечение 2х плоскостей. D= Найти Точку пересечения прямой D и плоскости α. Прямая пересекает плоскость в 1м месте, если направляющий вектор А, прямой D не перпендикулярен нормальному вектору n плоскости. (n,a)≠0, тогда есть точка пересечения. Для нахождения необходимо приравнять параметрическое уравнение прямой к уравнению плоскости.
Найти координаты проекции в точке Р(1.0.1) на плоскость Проекция P есть точка пересечения прямой D проходящей через точку Р и плоскость α. Нормаль к Найти точку симметричную точке Р(1.-1.3) относительно прямой d: 1(x-0)-1(y+1)+1(z-3)=0 α: x-y+z-4=0 Теперь найдем точку пересечения прямой и плоскости приравняв уравнения прямой и плоскости. Q=(2;-1;1) Вектор PQ равен вектору P1Q Следовательно Q – середина PP1 X(q)= Взаимное расположение прямых в пространстве. Прямые а || b если их направляющие векторы ||. Найдем расстояние от точки Мо(xo,yo,zo) до прямой D в пространстве. D= H= Расстояние между скрещивающимися прямыми. А: = Их направляющие вектора равны a1 и a2 Возьмем 2 точки М1 на а и М2 на b M1M2={x2-x1;y2-y1;z2-z1} H=
4. Определители n-го порядка. Вычисление и свойства. n-порядок определяется в матрице по кол-ву строк и столбцов квадратной матрицы(число строк и столбцов равны). Определитель матрицы – это число, которое постоянно в соответствии целой таблице, т.е. матрицы. Определитель 1го порядка равен элементу матрицы. Определитель 2го порядка – произведение главной диагонали – произведение побочной диагонали. Определитель 3го порядка: метод треугольн. Определитель не может быть разным у одной и той же матрици каким бы способом его не высчитывали. Минором какой-либо квадратной матрицы называется определитель, полученный из матрицы путем вычеркивания строки и столбца на котором он находится Алгебраическим дополнением какого-либо элемента квадратной матрицы является минор этой матрицы, умноженный на (-1) в стпени №строки+№столбца на пересечении которых он находится. Свойства определителей: 1) Определитель не поменяется, если матрицу транспонировать 2) Перестановка любых 2х строк или столбцов равносильна умножению определителя на -1. 3) Если в матрице 2 одинаковые строки или столбцы, то опред. = 0. Док-во, т.к. мы меняем местами одинак строки, то опред * на (-1), но строки не меняются, следоват-но определит. = 0. 4) Если каждый элемент какой-либо строки-столбца определителя умножить на действит число α, то это равносильно произведению всего определителя на число α. 5) Если в матрице есть 0вая строка или столбец, то опред=0 6) Если в матрице есть пропорциональные строки, то определитель = 0 7) Если каждый элемент какого-либо столбца(строки) матрицы представляет собой сумму 2х слагаемых, то определ. Можно представить в виде суммы 2х определителей. 8) Величина определителя не изменится, если к столбцу, строке прибавить другую стоку, столбец умноженное на действительное число α. 9) Величина определителя численно равна сумме элементов какой-либо строки или столбца, умноженное на свои алгебр. Дополнения. Разложение определителя по какой-либо строке или столбцу. Определители 4 и более высокого порядка можно вычислить только разложением по строке или столбцу. Перечисленные свойства справедливы для определителей любых порядков больше 1.
Пример Для облегчения расчетов выбираем столб, где есть хотя бы один 0. Определитель треугольной матрицы равен произведению элементов на главной диагонали или элементов на побочной диагонали умножен. На (-1). Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали. Определитель AB равен определителю А умноженный на определитель B.Для нахождения определителя необходимо выделить строку или столбец где больше всего 0,далее как показано в примере сверху.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.19 (0.01 с.) |

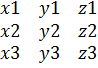 | = x1*|
| = x1*| 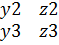 | - y1*|
| - y1*| 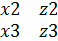 |+ z1* |
|+ z1* | 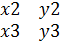 |
| A(x-x0)+B(y-y0)+c(z-z0)=0 Мо{x0,y0,z0} n{A,B,C} M{x,y,z}
A(x-x0)+B(y-y0)+c(z-z0)=0 Мо{x0,y0,z0} n{A,B,C} M{x,y,z}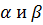 – угол, полученный при пересечении этих плоскостей, причем 1 из углов будет равен углу при пересечении нормальных векторов n1 и n2.
– угол, полученный при пересечении этих плоскостей, причем 1 из углов будет равен углу при пересечении нормальных векторов n1 и n2.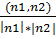 ) =
) = 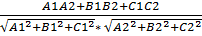
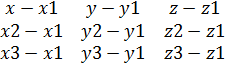 | Решаем уравнение, приравниваем к 0 и получаем уравнение плоскости.
| Решаем уравнение, приравниваем к 0 и получаем уравнение плоскости.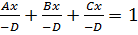 Вынесем в знаменатель A,B,C
Вынесем в знаменатель A,B,C – уравнение плоскости α в отрезках отсекаемых этой плоскостью от координатных осей. Плоскость заданную таким образом легко строить, т.к. она проходит через точки (a;0;0),(0;b;0), (0;0;c)
– уравнение плоскости α в отрезках отсекаемых этой плоскостью от координатных осей. Плоскость заданную таким образом легко строить, т.к. она проходит через точки (a;0;0),(0;b;0), (0;0;c)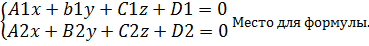
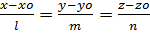
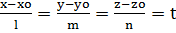
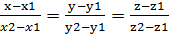 =t Параметрическое уравнение прямой: x=tx2-tx1+x1
=t Параметрическое уравнение прямой: x=tx2-tx1+x1 : 4x+6y+4z-25=0
: 4x+6y+4z-25=0 - направляющий вектор прямой D. Составляем параметрическое уравнение прямой и решаем систему.
- направляющий вектор прямой D. Составляем параметрическое уравнение прямой и решаем систему.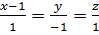 Строим плоскость α, которой будет принадлежать точка Р, причем α перпендикулярна d, cледовательно нормальный вектор к плоскости α равен направляющему вектору прямой D. N=a{1;-1;1} ур-е плоскости
Строим плоскость α, которой будет принадлежать точка Р, причем α перпендикулярна d, cледовательно нормальный вектор к плоскости α равен направляющему вектору прямой D. N=a{1;-1;1} ур-е плоскости Находим Xp1 также для координат y и z и получаем точку симметричную данной относительно прямой.
Находим Xp1 также для координат y и z и получаем точку симметричную данной относительно прямой.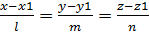 M1(x1,y1,z1) a1||a a1принадлежит d достроим до параллелограмма М1Мо={xo-x1,yo-y1,z0-z1} s=|[M1Mo,a]| s=|a1|*h
M1(x1,y1,z1) a1||a a1принадлежит d достроим до параллелограмма М1Мо={xo-x1,yo-y1,z0-z1} s=|[M1Mo,a]| s=|a1|*h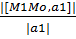
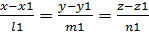 B:=
B:= 
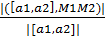
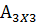 =
= 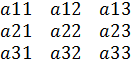
 =
=  и т.д.
и т.д. = 4*
= 4* 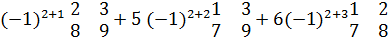 =0
=0


