
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет 9 размерность линейного подпространства. Ранг матрицы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Число k называется размерностью линейного подпространства L, еслив L существует система из k линейно независимых векторов, а любые k+ 1 вектора — линейно зависимы. Обозначаемdim L=k. Нетрудно доказать следующее утверждение. Теорема. В k-мерном линейном подпространстве существует базис их k векторов. Доказательство теоремы. Действительно, если dim L=k, то существует система из k линейно независимых векторов Справедливы также следующие утверждения (оставим их без доказательства). Теорема. Любая упорядоченная система из k линейно независимых векторов k-мерного линейного подпространства является базисом в этом подпространстве. Теорема. Размерность линейного подпространства равна числу векторов в базисе этого подпространства. Отсюда следует: dim(Rn) = n. Действительно, в пространстве Rn есть базис из n векторов — естественный базис в Rn. Пример. Размерность линейного подпространства L арифметических векторов из Rn, у которых последние компоненты — нулевые, равна n – 1. Действительно, векторы Тогда можно использовать другое определение базиса. Определение. Любая упорядоченная линейно независимая система из k векторов k-мерного линейного подпространства L образует базис этого линейного подпространства L. Это означает, что если dimL=k и арифметические векторы Подпространство строк и подпространство столбцов прямоугольной матрицы Рассмотрим прямоугольную матрицу Am, n, у которой m строк и n столбцов:
Её строки — А столбцы — Понятно, что множество строк матрицы Am, n, к которому добавили все строки, которые могут быть получены при элементарных преобразованиях матрицы (исключая транспонирование) — линейное подпространство в Rn. А аналогично образованное множество столбцов — линейное подпространство в Rm.
Это означает, что мы можем говорить о линейной зависимости и о линейной независимости строк и столбцов матрицы, о размерности подпространства строк и подпространства столбцов матрицы, о базисах в соответствующих подпростьранствах. Ранг матрицы Определение. Ранг матрицы равен максимальному числу линейно независимых строк матрицы. Обозначаем Rg A, rg A. Т.е., если ранг матрицы равен r, то среди строк матрицы есть r линейно независимых строк, а любые r +1 строки — линейно зависимы. Определение. Матрицы, имеющие одинаковый ранг, называются подобными. Утверждение. Элементарные преобразования не меняют ранга матрицы. Доказательство утверждения. Пусть Am, n — прямоугольная матрица и Rg A = r. Не умаляя общности, положим — линейно независимы первые r строк: Выполним такое преобразование: к одной из строк матрицы прибавим другую, умноженную на отличное от нуля число. Сначала выполним такое преобразование с первыми r линейно независимыми строками. Например, Т.к. строки поскольку строки
Если же
Утверждение доказано. Теорема. Ранг матрицы равен числу ненулевых строк в ступенчатой форме матрицы. Доказательство теоремы. Рассмотрим ступенчатую матрицу
т.е. Первые r строк этой матрицы линейно независимы. Действительно, приравняем к нулю линейную комбинацию этих строк:
Равенство нулю линейной комбинации возможно тогда и только тогда, когда:
Итак, первые r ненулевые строки линейно независимы, а любые r +1 строки — линейно зависимы, т.к. линейно зависима любая система векторов, содержащая нулевой вектор. Теорема доказана. Отсюда — алгоритм вычисления ранга матрицы. Приведем матрицу к ступенчатому виду (доказано, что это можно сделать гауссовым исключением), ранг исследуемой матрицы равен рангу ступенчатой матрицы (выше доказано, что элементарные преобразования не меняют ранга матрицы), ранг ступенчатой матрицы равен числу ненулевых строк в ступенчатой форме матрицы (по только что доказанной теореме).
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 2034; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.176 (0.011 с.) |

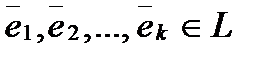 , а любая система из k +1 вектора
, а любая система из k +1 вектора 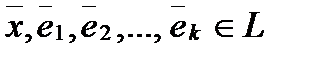 — линейно зависима, но тогда любой вектор
— линейно зависима, но тогда любой вектор  линейно выражается через векторы:
линейно выражается через векторы:  , т.е.
, т.е. 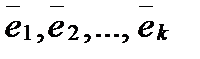 — базис в L.
— базис в L. — очевидно, принадлежат L и линейно независимы. Покажем, что они образуют базис в L. Для произвольного вектора
— очевидно, принадлежат L и линейно независимы. Покажем, что они образуют базис в L. Для произвольного вектора  имеет место разложение справедливо:
имеет место разложение справедливо:  , т.е. векторы
, т.е. векторы  образуют базис в L. В этом базисе n -1 вектор, следовательно, dim L = n –1.
образуют базис в L. В этом базисе n -1 вектор, следовательно, dim L = n –1. из L линейно независимы, то для любого
из L линейно независимы, то для любого  существует единственный набор чисел
существует единственный набор чисел  таких, что
таких, что 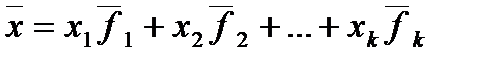 .
.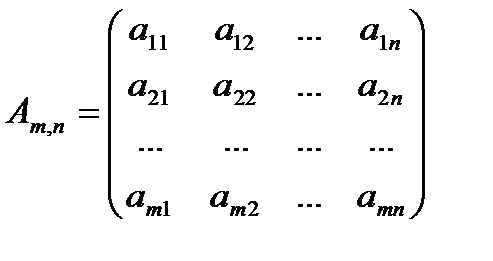 .
. —являются векторами из Rn,
—являются векторами из Rn,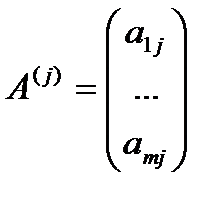 — являются векторами из Rm.
— являются векторами из Rm. . Выполним элементарные преобразования строк матрицы. Обозначим полученную матрицу A’, ее строки —
. Выполним элементарные преобразования строк матрицы. Обозначим полученную матрицу A’, ее строки —  .Очевидно, что перестановка строк или умножение строки на число не может повлиять на количество линейно независимых строк.
.Очевидно, что перестановка строк или умножение строки на число не может повлиять на количество линейно независимых строк. . Тогда
. Тогда 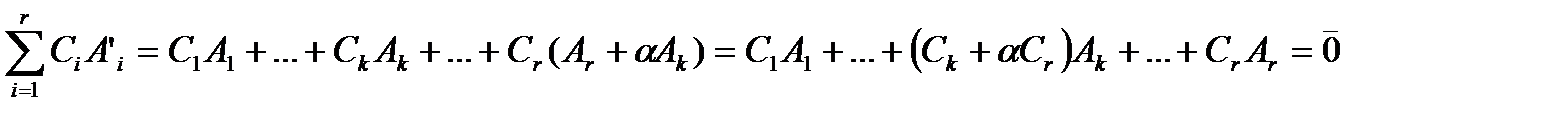
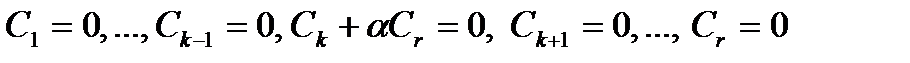 . Отсюда немедленно следует, что и
. Отсюда немедленно следует, что и  , т.е. первые r строк преобразованной матрицы
, т.е. первые r строк преобразованной матрицы  — линейно независимы. Покажем, что любая система
— линейно независимы. Покажем, что любая система  строк преобразованной матрицы линейно зависима, т.е. покажем, что строка
строк преобразованной матрицы линейно зависима, т.е. покажем, что строка  линейно выражается через строки
линейно выражается через строки  :
: линейно зависимы, то
линейно зависимы, то , а отсюда —
, а отсюда —  и
и
 , то первые r строк преобразованной матрицы линейно независимы, а любые r+ 1линейно зависимы, т.к. любая строка преобразованной матрицы линейно выражается через ее первые r линейно независимых строк:
, то первые r строк преобразованной матрицы линейно независимы, а любые r+ 1линейно зависимы, т.к. любая строка преобразованной матрицы линейно выражается через ее первые r линейно независимых строк:

 ,
,  для всех
для всех 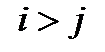 , и
, и 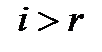 . Важно понимать, то у ступенчатой матрицы первые r диагональных элементовотличны от нуля:
. Важно понимать, то у ступенчатой матрицы первые r диагональных элементовотличны от нуля:  .
.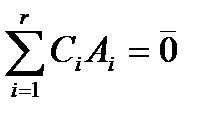 и вычислим ее в естественном базисе:
и вычислим ее в естественном базисе: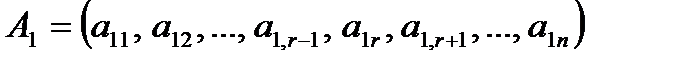 ,
,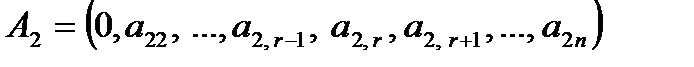 , …,
, …,

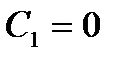 , поскольку
, поскольку  ,
, , поскольку
, поскольку 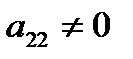 , …,
, …,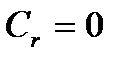 , поскольку
, поскольку 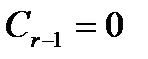 и
и  .
.


