

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Решение нелинейного уравнения с одной неизвестной. Методы отделения и уточнения корней.
Похожие статьи вашей тематики
ЛАБОРАТОРНАЯ РАБОТА №1
Решение нелинейного уравнения с одной неизвестной. Методы отделения и уточнения корней.
Постановка задачи. Для данного нелинейного уравнения y(x)=0 с одной неизвестной величиной на промежутке [a,b] отделить корни с шагом h (Шаговым методом)и уточнить корень с точностью ε:
- методом половинного деления
- методом Ньютона
- методом простой итерации
Идея метода
| Название метода
| Выбор начального значения
| Итерационная формула
| Окончание процесса вычисления
| | Шаговый метод
| x=a
| y=f(x) – значение функция в точке x
x1=x+h – следующее значение переменной x
y1=f(x1) - значение функция в точке x1
y*y1<0 - признак интервала изоляции
| x1<=b
| | Метод половинного деления
| [a,b] – интервал изоляции
| x=(a+b)/2 – середина интервала
f(a) – значение функции в точке a
f(x) – значение функции в точке x
если f(a)*f(x)<0, то выбираем [a,x]
если f(a)*f(x)>0, то выбираем [x,b]
| |f(x)|<ε
| | Метод Ньютона
| x0 = a или x0 = b
f2(x)- вторая производная функции f(x)
f(x0)*f2(x0)>0
| f1(x) – первая производная функции f(x)
xi+1 = xi - f(xi)/f1(xi)
| |f(xi)|<ε
| | Метод простой итерации
(1 способ)
| привести уравнение к виду
x= φ(x)
x0 = a или x0 = b
|φ(a)|<1
|φ(b)|<1
если |φ(a)| > |φ(b)|, то x0=a
если |φ(a)| < |φ(b)|, то x0=b
| xi+1= φ(xi)
| |f(xi)|<ε
| | Метод простой итерации
(2 способ)
| f1(x) – первая производная функции f(x)
если |f1(a)| > |f1(b)|, то x0=a
если |f1(a)| < |f1(b)|, то x0=b
| с=1/max(|f1(a)|;|f1(b)|)
xi+1 = xi – c*f(xi)
| |f(xi)|<ε
|
Шаговый метод .
Постановка задачи: шаговым методом найти интервал изоляции корня нелинейного уравнения ln(x) - 2·x + 2,5 = 0 на интервале [1; 2], шаг h = 0,1.

| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
int main()
{ double a,b,x0,x1,h;
int N;
cout<<"Vvedite a b"<<endl;
cin>>a>>b;
cout<<"Vvedite chislo razbien"<<endl;
cin>>N;
h=(b-a)/N;
cout.precision(5);
cout.setf(ios::left);
cout<<"_____________________________________"<<endl;
cout<<setw(12)<<"x"<<setw(12)<<"F(x)"<<endl;
cout<<"_____________________________________"<<endl;
x0=a;
cout<<setw(12)<<x0<<setw(12)<<F(x0)<<endl;
while(x1<=b)
{
x1=x0+h;
cout<<setw(12)<<x1<<setw(12)<<F(x1)<<endl;
if(F(x0)*F(x1)<0)
cout<<"na interv ["<<x0<<","<<x1<<"] est koren"<<endl;
x0=x1;
}
return 0;}
|
Метод половинного деления
Постановка задачи: найти корень нелинейного уравнения
ln(x) - 2·x + 2.5 =0
на отрезке [1; 2] методом половинного деления с точностью е = 0,001.

| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
int main()
{ double a,b,x,eps;
int k=0;
cout<<"Vvedite a b"<<endl;
cin>>a>>b;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout.precision(5);
cout.setf(ios::left);
cout<<"___________________________"<<endl;
cout<<setw(12)<<"a"<<setw(12)<<"x"<<setw(12)<<"b"
<<setw(12)<<"F(a)"<<setw(12)<<"F(x)"<<setw(12)<<
"F(b)"<<endl;
cout<<"___________________________"<<endl;
while(fabs(a-b)>eps)
{x=(a+b)/2;
cout<<setw(12)<<a<<setw(12)<<x<<setw(12)<<b
<<setw(12)<<F(a)<<setw(12)<<F(x)<<setw(12)<<
F(b)<<endl;
if(F(a)*F(x)<0)
b=x;
else
a=x;
k++;
}
cout<<endl<<"koren="<<x<<" F("<<x<<")="<<F(x);
cout<<endl<<"max chislo iter"<<k;
return 0;}
|
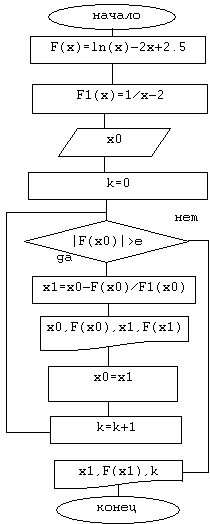
Метод Ньютона
Постановка задачи: найти корень нелинейного уравнения
ln(x) - 2·x + 2,5 = 0
на отрезке [1; 2 ] методом Ньютона с точностью е = 0,001.
| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
double F1 (double x)
{ return (1/x-2);}
int main()
{ double x0,x1,eps;
int k=0;
cout<<"Vvedite nachal znach"<<endl;
cin>>x0;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout.precision(5);
cout.setf(ios::left);
cout<<"______________________________"<<endl;
cout<<setw(12)<<"x0"<<setw(12)<<"F(x0)"<<setw(12)
<<"x1"<<setw(12)<<"F(x1)"<<endl;
cout<<"______________________________"<<endl;
while(fabs(F(x0))>eps)
{
x1=x0-F(x0)/F1(x0);
cout<<setw(12)<<x0<<setw(12)<<F(x0)<<setw(12)
<<x1<<setw(12)<<F(x1)<<endl;
x0=x1;
k++;
}
cout<<endl<<"koren="<<x1<<" F("<<x1<<")="<<F(x1)<<endl;
cout<<"vipolneno iter"<<k;
return 0;}
|
Метод простой итерации
Постановка задачи: найти корень нелинейного уравнения
ln(x) - 2·x + 2,5 = 0
на отрезке [1; 2 ] методом Ньютона с точностью е = 0,001.

| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
double S (double x)
{ return ((log(x)+2.5/2);}
int main()
{ double x0,x1,eps;
int k,kmax;
cout<<"Vvedite nachal znach"<<endl;
cin>>x0;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout<<"Vvedite max chislo iter"<<endl;
cin>>kmax;
cout.precision(5);
cout.setf(ios::left);
cout<<"______________________________"<<endl;
cout<<setw(12)<<"x0"<<setw(12)<<"F(x0)"<<setw(12)<<
"x1"<<setw(12)<<"F(x1)"<<endl;
cout<<"_______________________________"<<endl;
k=0;
while(fabs(F(x0))>eps)
{
x1=S(x0);
cout<<setw(12)<<x0<<setw(12)<<F(x0)<<setw(12)<<x1
<<setw(12)<<F(x1)<<endl;
if(k>kmax) {cout<<"vipolneno max iter"<<endl;
break;}
x0=x1;
k++;
}
cout<<endl<<"koren="<<x1<<" F("<<x1<<")="<<F(x1);
cout<<endl<<"chislo iter"<<k;
return 0;}
|
Лабораторная работа №2
Метод Гаусса
Постановка задачи: Дана система линейных уравнений
A11*x1+A12*x2+A13*x3+A14*x4=B1
A21*x1+A22*x2+A23*x3+A24*x4=B2
A31*x1+A32*x2+A33*x3+A34*x4=B3
A41*x1+A42*x2+A43*x3+A44*x4=B4
найти точное решение методом Гаусса.
Запись системы линейных уравнений в матричном виде
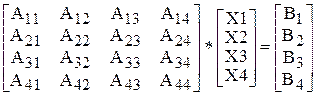

| Программа на языке CИ
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{ double a[4][4]={{5,1,1,1},{1,7,1,1},{1,1,6,1},{1,1,1,4}};
double b[4]={8,10,9,7};
double x[4];
int n,k,i,j;
n=4;
double c,s;
for(k=0;k<n-1;k++)
for(i=k+1;i<n;i++)
{
c=a[i][k]/a[k][k];
a[i][k]=0;
for(j=k+1;j<n;j++)
a[i][j]=a[i][j]-c*a[k][j];
b[i]=b[i]-c*b[k];
}
x[n-1]=b[n-1]/a[n-1][n-1];
for (i=n-1;i>=0;i--)
{
s=0;
for(j=i+1;j<n;j++)
{s=s+a[i][j]*x[j];
x[i]=(b[i]-s)/a[i][i];
}
}
cout<<"reshenie"<<endl;
for (i=0;i<n;i++)
cout<<x[i];
return 0;}
|

| Метод простой итерации.
Постановка задачи: Дана система линейных уравнений. Найти приближённое решение с точностью е.
Программа на языке CИ
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{ double
A[4][4]={{5,1,1,1},{1,7,1,1},{1,1,6,1},{1,1,1,4}};
double B[4]={8,10,9,7};
double X0[4],X1[4];
double eps,tochnost,max_tochnost,s;
int k,kmax,i,j;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout<<"Vvedite max chislo iter"<<endl;
cin>>kmax;
cout.precision(5);
cout.setf(ios::left);
for(i=0;i<4;i++) X0[i]=0;
k=0;
while(fabs(max_tochnost)>eps)
{
if(k>=kmax) break;
k=k+1;
cout<<setw(5)<<k;
max_tochnost=-100;
for(i=0;i<4;i++)
{s=0;
for(j=0;j<4;j++)
if(i!=j) s=s+A[i][j]*X0[j];
X1[i]=(B[i]-s)/A[i][i];
cout<<setw(10)<<X1[i];
tochnost=fabs(X1[i]-X0[i]);
if(tochnost>max_tochnost)
max_tochnost=tochnost;
}
cout<<endl;
for(i=0;i<4;i++) X0[i]=X1[i];
}
cout<<endl;
cout<<"Otvet"<<endl;
for(i=0;i<4;i++)
cout<<setw(10)<<X1[i];
cout<<endl;
cout<<"Chislo iter="<<k;
return 0;}
| 
| Метод Зейделя.
Постановка задачи: Дана система линейных уравнений. Найти приближённое решение с точностью е.
Программа на языке CИ
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{ double A[4][4]={{5,1,1,1},{1,7,1,1},{1,1,6,1},{1,1,1,4}};
double B[4]={8,10,9,7};
double X0[4],X1[4];
double eps,tochnost,max_tochnost,s;
int k,kmax,i,j;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout<<"Vvedite max chislo iter"<<endl;
cin>>kmax;
cout.precision(5);
cout.setf(ios::left);
for(i=0;i<4;i++) X0[i]=0;
k=0;
while(fabs(max_tochnost)>eps)
{
if(k>=kmax) break;
k=k+1;
cout<<setw(5)<<k;
max_tochnost=-100;
for(i=0;i<4;i++)
{s=0;
for(j=0;j<4;j++)
if(i!=j) s=s+A[i][j]*X0[j];
X1[i]=(B[i]-s)/A[i][i];
cout<<setw(10)<<X1[i];
tochnost=fabs(X1[i]-X0[i]);
if(tochnost>max_tochnost)
max_tochnost=tochnost;
X0[i]=X1[i];
}
cout<<endl;
}
cout<<endl;
cout<<"Otvet"<<endl;
for(i=0;i<4;i++)
cout<<setw(10)<<X1[i];
cout<<endl;
cout<<"Chislo iter="<<k;
return 0;}
| | | | | | |
Лабораторная работа №3
Метод наименьших квадратов
| Название метода
| Система для нахождения коэффициентов полинома
| Ответ
| | Метод наименьших квадратов
(аппроксимация)
| полином 1 степени
 полином 2 степени
полином 2 степени

| P1(x)=a0+a1*x
P2(x)=a0+a1*x+a2*x2
| 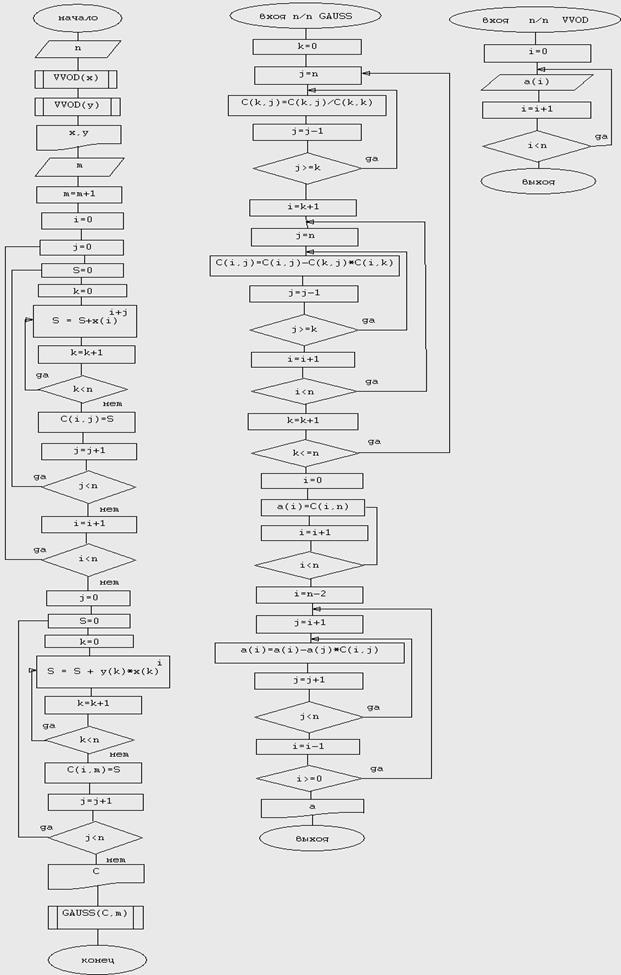
Программа на языке СИ
| #include <iostream.h>
#include <iomanip.h>
#include <math.h>
void gauss(double **c, int n)
{
int i,j;
cout.precision(3);
int k;
for (k=0; k<n; k++){
for (j=n; j>=k; j--)
c[k][j]/=c[k][k];
for (i=k+1; i<n; i++)
for (j=n; j>=k; j--)
c[i][j]-=c[k][j]*c[i][k];
}
double *a;
a=new double[n*sizeof(double)];
//Обратный ход
for (i=0; i<n; i++)
a[i]=c[i][n];
for (i=n-2; i>=0; i--)
for (j=i+1; j<n; j++)
a[i]-=a[j]*(c[i][j]);
//Печать результата
cout<<"Koeff\n";
for (j=0; j<n; j++)
cout<<"a"<<j<<"="<<a[j]<<endl;
delete[] a;
}
void vvod(double *a, int n)
{
for(int i=0;i<n;i++)
cin>>a[i];
}
int main()
{
int n,i,j;
cout<<"kol-vo tochek"<<endl;
cin>>n;
double **c;
double *x, *y;
x= new double[n];
cout<<"vvod x"<<endl;
vvod(x,n);
y= new double[n];
cout<<"vvod y"<<endl;
vvod(y,n);
| cout<<endl<<"prover'te koord tochek"<<endl;
for(i=0;i<n;i++)
cout<<"("<<x[i]<<","<<y[i]<<")"<<endl;
int m;
cout<<"stepen polinoma m"<<endl;
cin>>m;
m=m+1; //esli m=1, to yr-ya 2
c= new double *[m];
for(i=0;i<m;i++)
c[i]=new double[m];
int k;
double s;
for(i=0;i<m;i++)
for(j=0;j<m;j++){
s=0;
for(k=0;k<n;k++)
{
s=s+pow(x[k],(i+j));}
c[i][j]=s;}
for(i=0;i<m;i++){s=0;
for(k=0;k<n;k++)
{
s=s+y[k]*pow(x[k],i);}
c[i][m]=s;}
cout<<"Matritsa C+Y"<<endl;
for(i=0;i<m;i++)
{for(j=0;j<m+1;j++)
cout<<setw(5)<<c[i][j]<<" ";
cout<<endl;
}
cout<<endl;
gauss(c,m);
delete[] x;
delete[] y;
// for(i=0;i<n;i++)
// delete c[i];
delete[] c;
cin.get();
cin.get();
return 0;}
|
Программа на языке СИ
| #include <iostream.h>
#include <iomanip.h>
#include <math.h>
void gauss(double **c, int n)
{
int i,j;
cout.precision(3);
int k;
for (k=0; k<n; k++){
for (j=n; j>=k; j--)
c[k][j]/=c[k][k];
for (i=k+1; i<n; i++)
for (j=n; j>=k; j--)
c[i][j]-=c[k][j]*c[i][k];
}
double *a;
a=new double[n*sizeof(double)];
//Обратный ход
for (i=0; i<n; i++)
a[i]=c[i][n];
for (i=n-2; i>=0; i--)
for (j=i+1; j<n; j++)
a[i]-=a[j]*(c[i][j]);
//Печать результата
cout<<"Koeff\n";
for (j=0; j<n; j++)
cout<<"a"<<j<<"="<<a[j]<<endl;
delete[] a;
}
void vvod(double *a, int n)
{
for(int i=0;i<n;i++)
cin>>a[i];
}
int main()
| {
int n,i,j;
cout<<"kol-vo tochek"<<endl;
cin>>n;
double **c;
double *x, *y;
x= new double[n*sizeof(double)];
cout<<"vvod x"<<endl;
vvod(x,n);
y= new double[n*sizeof(double)];
cout<<"vvod y"<<endl;
vvod(y,n);
cout<<endl<<"prover'te koord tochek"<<endl;
for(i=0;i<n;i++)
cout<<"("<<x[i]<<","<<y[i]<<")"<<endl;
c= new double *[n];
for(i=0;i<n;i++)
c[i]=new double[n];
for(i=0;i<n;i++)
{
for(j=0;j<n;j++) c[i][j]=pow(x[i],j);
c[i][n]=y[i];
}
cout<<"Matritsa C+Y"<<endl;
for(i=0;i<n;i++)
{for(j=0;j<n+1;j++)
cout<<setw(7)<<c[i][j];
cout<<endl;}
cout<<endl;
gauss(c,n);
delete[] x;
delete[] y;
// for(i=0;i<n;i++)
// delete c[i];
delete[] c;
cin.get();
cin.get();
return 0;
}
|
Лабораторная работа №4
Метод трапеций

| Программа на языке СИ
#include <iostream.h>
#include <math.h>
double F(double x)
{return(x);}
int main()
{double I0,I1,h,eps,a,b,x;
int n,j;
cout<<"Vvefite a i b"<<endl;
cin>>a>>b;
cout<<"Vvedite cislo razbieniy [a,b]"<<endl;
cin>>n;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
I0=1E+10;
I1=0;
while(fabs(I1-I0)>eps)
{
h=(b-a)/n;
I1=0;
for(j=1;j<n;j++)
{x=a+j*h;
I1=I1+F(x)*h;
}
I1=I1+h*(F(a)+F(b))/2;
n=2*n;
I0=I1;}
cout<<"Otvet I="<<I1<<endl;
return 0;}
|
Метод Симпсона.

| Программа на языке СИ
#include <iostream.h>
#include <math.h>
double F(double x)
{return(x);}
int main()
{double I0,I1,S1,S2,h,eps,a,b,x;
int n,j;
cout<<"Vvefite a i b"<<endl;
cin>>a>>b;
cout<<"Vvedite cislo razbieniy [a,b]"<<endl;
cin>>n;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
I0=1E+10;
I1=0;
while(fabs(I1-I0)>eps)
{
h=(b-a)/n;
S1=0;
for(j=1;j<=n-1;j+2)
{x=a+j*h;
S1=S1+F(x);
}
S2=0;
for(j=2;j<n;j+2)
{x=a+j*h;
S2=S2+F(x);
}
I1=(h/6)*(F(a)+F(b)+2*S1+4*S2);
n=2*n;
I0=I1;}
cout<<"Otvet I="<<I1<<endl;
return 0;}
|
Лабораторная работа №5
Содержание
Решение нелинейного уравнения с одной неизвестной. Методы отделения и уточнения корней. 3
Шаговый метод. 4
Метод половинного деления. 5
Метод Ньютона. 6
Метод простой итерации. 7
Решение систем линейных уравнений. Прямые и итерационные методы. 8
Метод Гаусса. 8
Метод простой итерации. 10
Метод Зейделя. 10
Аппроксимация и Интерполяции. 12
Метод наименьших квадратов. 12
Метод неопределённых коэффициентов. 14
Вычисление определённого интеграла. 17
Метод центральных прямоугольников. 18
Метод трапеций. 19
Метод Симпсона. 20
Обыкновенные дифференциальные уравнения. Численное решение задач с начальными условиями Коши. 21
Метод Эйлера. 22
Модифицированный метод Эйлера. 23
Модифицированный метод Эйлера. 235
Литература
1.Павловская Т.А. C/C++Программирование на языке высокого уровня: Учебник для вузов/ Павловская Т.А СПб. Изд.-во «Питер», 2007.
2. Павловская Т.А. C/C++Структурное программирование:практикум./: Павловская Т.А, Ю.В.Щупак СПб.: Изд.-во «Питер», 2007.
ЛАБОРАТОРНАЯ РАБОТА №1
Решение нелинейного уравнения с одной неизвестной. Методы отделения и уточнения корней.
Постановка задачи. Для данного нелинейного уравнения y(x)=0 с одной неизвестной величиной на промежутке [a,b] отделить корни с шагом h (Шаговым методом)и уточнить корень с точностью ε:
- методом половинного деления
- методом Ньютона
- методом простой итерации
Идея метода
| Название метода
| Выбор начального значения
| Итерационная формула
| Окончание процесса вычисления
| | Шаговый метод
| x=a
| y=f(x) – значение функция в точке x
x1=x+h – следующее значение переменной x
y1=f(x1) - значение функция в точке x1
y*y1<0 - признак интервала изоляции
| x1<=b
| | Метод половинного деления
| [a,b] – интервал изоляции
| x=(a+b)/2 – середина интервала
f(a) – значение функции в точке a
f(x) – значение функции в точке x
если f(a)*f(x)<0, то выбираем [a,x]
если f(a)*f(x)>0, то выбираем [x,b]
| |f(x)|<ε
| | Метод Ньютона
| x0 = a или x0 = b
f2(x)- вторая производная функции f(x)
f(x0)*f2(x0)>0
| f1(x) – первая производная функции f(x)
xi+1 = xi - f(xi)/f1(xi)
| |f(xi)|<ε
| | Метод простой итерации
(1 способ)
| привести уравнение к виду
x= φ(x)
x0 = a или x0 = b
|φ(a)|<1
|φ(b)|<1
если |φ(a)| > |φ(b)|, то x0=a
если |φ(a)| < |φ(b)|, то x0=b
| xi+1= φ(xi)
| |f(xi)|<ε
| | Метод простой итерации
(2 способ)
| f1(x) – первая производная функции f(x)
если |f1(a)| > |f1(b)|, то x0=a
если |f1(a)| < |f1(b)|, то x0=b
| с=1/max(|f1(a)|;|f1(b)|)
xi+1 = xi – c*f(xi)
| |f(xi)|<ε
|
Шаговый метод .
Постановка задачи: шаговым методом найти интервал изоляции корня нелинейного уравнения ln(x) - 2·x + 2,5 = 0 на интервале [1; 2], шаг h = 0,1.

| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
int main()
{ double a,b,x0,x1,h;
int N;
cout<<"Vvedite a b"<<endl;
cin>>a>>b;
cout<<"Vvedite chislo razbien"<<endl;
cin>>N;
h=(b-a)/N;
cout.precision(5);
cout.setf(ios::left);
cout<<"_____________________________________"<<endl;
cout<<setw(12)<<"x"<<setw(12)<<"F(x)"<<endl;
cout<<"_____________________________________"<<endl;
x0=a;
cout<<setw(12)<<x0<<setw(12)<<F(x0)<<endl;
while(x1<=b)
{
x1=x0+h;
cout<<setw(12)<<x1<<setw(12)<<F(x1)<<endl;
if(F(x0)*F(x1)<0)
cout<<"na interv ["<<x0<<","<<x1<<"] est koren"<<endl;
x0=x1;
}
return 0;}
|
Метод половинного деления
Постановка задачи: найти корень нелинейного уравнения
ln(x) - 2·x + 2.5 =0
на отрезке [1; 2] методом половинного деления с точностью е = 0,001.

| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
int main()
{ double a,b,x,eps;
int k=0;
cout<<"Vvedite a b"<<endl;
cin>>a>>b;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout.precision(5);
cout.setf(ios::left);
cout<<"___________________________"<<endl;
cout<<setw(12)<<"a"<<setw(12)<<"x"<<setw(12)<<"b"
<<setw(12)<<"F(a)"<<setw(12)<<"F(x)"<<setw(12)<<
"F(b)"<<endl;
cout<<"___________________________"<<endl;
while(fabs(a-b)>eps)
{x=(a+b)/2;
cout<<setw(12)<<a<<setw(12)<<x<<setw(12)<<b
<<setw(12)<<F(a)<<setw(12)<<F(x)<<setw(12)<<
F(b)<<endl;
if(F(a)*F(x)<0)
b=x;
else
a=x;
k++;
}
cout<<endl<<"koren="<<x<<" F("<<x<<")="<<F(x);
cout<<endl<<"max chislo iter"<<k;
return 0;}
|
Метод Ньютона
Постановка задачи: найти корень нелинейного уравнения
ln(x) - 2·x + 2,5 = 0
на отрезке [1; 2 ] методом Ньютона с точностью е = 0,001.

| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
double F1 (double x)
{ return (1/x-2);}
int main()
{ double x0,x1,eps;
int k=0;
cout<<"Vvedite nachal znach"<<endl;
cin>>x0;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout.precision(5);
cout.setf(ios::left);
cout<<"______________________________"<<endl;
cout<<setw(12)<<"x0"<<setw(12)<<"F(x0)"<<setw(12)
<<"x1"<<setw(12)<<"F(x1)"<<endl;
cout<<"______________________________"<<endl;
while(fabs(F(x0))>eps)
{
x1=x0-F(x0)/F1(x0);
cout<<setw(12)<<x0<<setw(12)<<F(x0)<<setw(12)
<<x1<<setw(12)<<F(x1)<<endl;
x0=x1;
k++;
}
cout<<endl<<"koren="<<x1<<" F("<<x1<<")="<<F(x1)<<endl;
cout<<"vipolneno iter"<<k;
return 0;}
|
Метод простой итерации
Постановка задачи: найти корень нелинейного уравнения
ln(x) - 2·x + 2,5 = 0
на отрезке [1; 2 ] методом Ньютона с точностью е = 0,001.

| Программа на языке CИ
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
double F (double x)
{ return (log(x)-2*x+2.5);}
double S (double x)
{ return ((log(x)+2.5/2);}
int main()
{ double x0,x1,eps;
int k,kmax;
cout<<"Vvedite nachal znach"<<endl;
cin>>x0;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout<<"Vvedite max chislo iter"<<endl;
cin>>kmax;
cout.precision(5);
cout.setf(ios::left);
cout<<"______________________________"<<endl;
cout<<setw(12)<<"x0"<<setw(12)<<"F(x0)"<<setw(12)<<
"x1"<<setw(12)<<"F(x1)"<<endl;
cout<<"_______________________________"<<endl;
k=0;
while(fabs(F(x0))>eps)
{
x1=S(x0);
cout<<setw(12)<<x0<<setw(12)<<F(x0)<<setw(12)<<x1
<<setw(12)<<F(x1)<<endl;
if(k>kmax) {cout<<"vipolneno max iter"<<endl;
break;}
x0=x1;
k++;
}
cout<<endl<<"koren="<<x1<<" F("<<x1<<")="<<F(x1);
cout<<endl<<"chislo iter"<<k;
return 0;}
|
Лабораторная работа №2
|







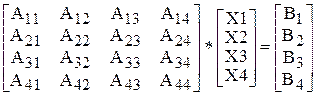



 полином 2 степени
полином 2 степени







