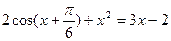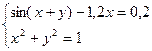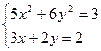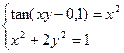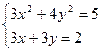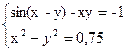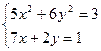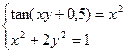Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение уравнений средствами MS EXCELСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель: изучить технологию численного решения уравнений средствами MS EXCEL. Теоретическое введение Пример 4.1. Нахождение корней полиномов при помощи табулирования и сервисной функции Подбор параметра. Известно, что если функция, определенная в интервале [a,b], имеет значения F(а) и F(b) с разными знаками, то в интервале [a,b] есть, по крайней мере, один корень. Построить алгоритм нахождения корней уравнений с заданной точностью EPS следующим образом. 1. Определить начальный интервал [A, B], где находятся корни. Для полиномов
модули всех корней xk, k = 1…n расположены в круговом кольце
где, Таким образом, положительные корни лежат в интервале [A, B], а отрицательные корни - в интервале [-B, -A]. 2. Табулируя полином в найденных начальных интервалах (например, с шагом (В-А)/10), составить таблицу {x, P(x)}. 3. Определить две соседние ячейки х, где функция меняет свой знак. Одно из значений (для которого значение функции ближе к нулю) принять за начальное приближение к корню полинома. 4. (меню Сервис). Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры (Сервис з Параметры з Вычисления) (рис. 4.1). 5. Открыть диалоговое окно Подбор параметра (рис. 4.2). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома. В поле Значение ввести 0 (т.е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, отведенной для переменной х, где должно находиться начальное приближение к корню полинома.
Рис. 4.1. Диалоговое окно Параметры
Рис. 4.2. Диалоговое окно Подбор параметра
Примечание. В этой ячейке должно содержаться числовое значение, а не формула, его вычисляющая. Для того, чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 4.3). В появившемся диалоговом окне отметить Значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра. 6. После подбора параметра (ОК) х получит значение корня. Процесс повторяется для всех найденных начальных приближений в диапазоне, определяемом формулой (4.1).
Рис. 4.3. Диалоговое окно Специальная вставка Пример 4.2. Нахождение корней нелинейных уравнений с помощью метода итераций. Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций уравнение представляют в виде x=F(x) и записывают итерационную схему
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, которое выбирается самостоятельно. Достаточное условие сходимости процесса: в окрестности корня | F /(x)| <1. Порядок действий в Excel может быть следующий. 1. Представить данное уравнение в виде x=F(x). 2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность. 3. В первую ячейку первой строки таблицы занести значение 0, во вторую – начальное приближение. 4. В следующие строки занести, соответственно, номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5). 5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения EPS. Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений – метод Ньютона. Его итерационная схема имеет вид
Сравнивая (4.2) и (4.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (4.3). В большинстве случаев метод Ньютона сходится быстрее. Пример 4.3. Нахождение корней нелинейных уравнений методом бисекции. Если метод итераций сходится не всегда, то метод бисекции (или метод деления отрезка пополам, или метод дихотомии) – безусловно сходящийся метод нахождения корней нелинейного уравнения F(x)=0, лишь бы был известен отрезок, на котором расположен корень уравнения. Пусть непрерывная функция F(x) меняет знак на концах отрезка [a,b], т.е. F(a)ЧF(b) < 0. Назовем такой отрезок отрезком локализации корня: на нем есть, по крайней мере, один корень. Найдем координату середины этого отрезка c=(a+b)/2 и рассмотрим два получившихся отрезка [a,c] и [c,b]. Если F(a)ЧF(с) < 0, то корень находится на отрезке [a,c], в противном случае – на отрезке [с,b]. Процесс деления все новых и новых отрезков локализации корня продолжаем до тех пор, пока длина отрезка не станет меньше заданной величины точности решения EPS.
Пример 4.4. Решение систем линейных алгебраических уравнений. В Excel имеются специальные функции для работы с матрицами (Вставка функции пМатематические): МОБР вычисление обратной матрицы А-1; МОПРЕД вычисление определителя матрицы D; МУМНОЖ нахождение произведения двух матриц. С их помощью можно решать системы линейных алгебраических уравнений вида
или в матричном виде АЧХ=В, где А = {aij}– матрица коэффициентов при неизвестных; В = {bij} – вектор-столбец правых частей уравнений; Х = {xij} – вектор-столбец неизвестных. Способ 1 (метод обратной матрицы). Решение имеет вид Х = А–1ЧВ, где А–1 – матрица, обратная по отношению к матрице А. С помощью функции МОБР находится обратная матрица, а затем с помощью функции МУМНОЖ она перемножается с вектором-столбцом правых частей уравнений. Примечание. При работе с матрицами перед вводом формулы необходимо выделить область на рабочем листе, куда будет выведен результат вычисления, а после задания исходных данных в поле функции выйти не как обычно, нажатием клавиши Enter или кнопки ОК, а нажатием клавиш Ctrl + Shift + Enter. Способ 2 (правило Крамера). Если определитель D, составленный из коэффициентов при неизвестных, отличен от нуля, то решение имеет вид x j = Dj / D, j=1...n. (4.5) Здесь Dj – дополнительный определитель, полученный из главного определителя системы D путем замены его j-го столбца вектором-столбцом В. С помощью функции МОПРЕД находятся главный и дополнительные определители, и по формулам (4.5) вычисляются корни СЛАУ. Способ 3 (метод исключений Гаусса). Этот метод основан на приведении матрицы системы к треугольному виду, что достигается последовательным исключением неизвестных из уравнений системы. Предположим, что в (4.4) a11 ¹ 0. Разделим первое уравнение системы на a11 (этот коэффициент называется ведущим или главным элементом), получим:
Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент ai1 (i=2,3,¼, n). Эти n–1 уравнений принимают вид:
Далее аналогичную процедуру выполняют с этой системой, оставляя в покое первое уравнение. Только теперь делят на другой ведущий элемент a22(1) ¹0. В результате исключения неизвестных приходим к СЛАУ с верхней треугольной матрицей с единицами на главной диагонали:
Индексы над коэффициентами означают, сколько раз данное уравнение преобразовывалось. Прямой ход метода Гаусса завершен. Обратный ход метода Гаусса заключается в нахождении неизвестных xn, xn-1,..., x1, причем в указанном порядке. В этом списке xn уже определено из последнего уравнения системы (4.6), а общая формула обратного хода имеет вид:
Проиллюстрируем этот алгоритм на примере решения системы из трех уравнений. 1.Располагаем на листе Excel матрицу коэффициентов и столбец правых частей (т.н. расширенная матрица 3´4), например, в ячейках А4:D6 (рис. 4.4). 2.Выделяем диапазон ячеек А8:D8 и вводим формулу: {=A4:D4/A4}. Фигурные скобки появляются автоматически при вводе формулы комбинацией клавиш Shift+Ctrl+Enter, как признак того, что идет работа не с отдельными ячейками, а с массивами.
3.Выделяем диапазон ячеек А9:D9, вводим формулу: {=A5:D5-$A$8:$D$8*B5} и копируем эту формулу в диапазон ячеек А10:D10. В ячейках А9 и А10 появились нули. 4.В ячейки А12:D12 копируем значения первой строки расширенной матрицы А8:D8, в ячейки А13:D13 – формулу {=A9:D9/B9}. При этом второй элемент главной диагонали матрицы коэффициентов становится равным единице.
Рис.4.4 – Результаты решения СЛАУ В ячейки А14:D14 вводим формулу: {=A10:D10–$A$13:$D$13*B10}. 5)В ячейки А16:D17 копируем значения первых двух строк расширенной матрицы (А12:D13), а в ячейки А18:D18 – формулу: {=A14:D14/C14}. Прямой ход метода Гаусса завершен: получилась верхняя треугольная матрица с диагональными элементами, равными 1.
Задание 4.5. Решение систем нелинейных уравнений. С помощью сервисной программы Поиск решения (Сервис | Поиск решения) в Excel можно решать системы нелинейных уравнений. В общем случае система нелинейных уравнений имеет вид:
Составим новую функцию F(x1, х2,..., хn), представляющую собой сумму квадратов правых частей уравнений:
Очевидно, переменные x1, х2,..., хn, являющиеся решением системы (4.7), с необходимостью и достаточностью являются также решением уравнения:
Технология решения. На листе Excel отводим ячейки для неизвестных данной системы уравнений, например с А1 по А5 (если пять переменных), и вводим туда начальные приближения. В ячейку В2 вводим формулу, вычисляющую функцию (4.8). Открываем диалоговое окно Поиск решения (рис. 4.5). В поле Установить целевую ячейку вводим В2, в группе Равной устанавливаем переключатель в положение Значению и в поле ввода задаем 0. В поле Изменяя ячейки вводим диапазон ячеек А1:А5.
Рис.4.5. Диалоговое окно Поиск решения при решении нелинейного уравнения
После нажатия на кнопку Выполнить будет найдено решение, которое поместится в ячейки А1:А5. В ячейке В2 будет вычислено значение левой части уравнения (4.9) с относительной погрешностью, задаваемой в диалоговом окне Параметры поиска решения. Примечание 1. При неудачном выборе вектора начального приближения решение может быть не найдено. Поэтому необходим предварительный анализ системы уравнений с целью определения лучшего (более близкого к корню) начального приближения. Например, для системы из двух уравнений можно затабулировать функцию (4.8) и в качестве начальных выбрать приближения, наиболее близкие к нулю. Примечание 2. Система уравнений может иметь несколько корней, поэтому необходим ее анализ и с этой стороны. Задавая разные начальные приближения, можно получить разные решения системы.
4.2. задания для практической работы Задание 4.1. Найти корни полиномов при помощи табулирования и сервисной функции Подбор параметра. Данные для решения взять из таблицы 4.1. Корни найти с точностью EPS=0,00001. Таблица 4.1 Полиномы
Задание 4.2. Найти корни нелинейных уравнений с помощью метода итераций. Данные для решения взять из таблицы 4.2. Точность решения EPS=0,0001. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат – очередное приближение к корню. Задание 4.3. Найти корни нелинейных уравнений методом бисекции. Таблица 4.2 Нелинейные уравнения
При использовании Excel достаточно внести в некоторые ячейки, лежащие в одной строке, формулы, осуществляющие: - вычисление значений левой и правой границы отрезков локализации; - нахождение середины отрезка; - вычисление произведения значений функций в левой и правой границах отрезка (для контроля правильности алгоритма); - проверку на точность решения (аналогично предыдущему заданию). Затем формулы копируются вниз по столбцам до тех пор, пока не будет найден корень с заданной степенью точности EPS=0,0001. Данные для решения взять из таблицы 4.2, то есть решить одно и то же уравнение двумя способами. Задание 4.4. Решить тремя способами систему линейных алгебраических уравнений, взяв данные для решения из таблицы 4.3. Проверить найденное решение умножением матрицы коэффициентов на вектор-столбец решения.
Таблица 4.3 Системы линейных алгебраических уравнений
Задание 5. Решить систему нелинейных уравнений, взяв данные из таблицы 1.4. Проверить найденное решение.
Таблица 1.4. Системы нелинейных уравнений
4.3.Контрольные вопросы 1. Опишите технологию нахождения корней полиномов при помощи табулирования и сервисной функции Подбор параметра. 2. С помощью какой сервисной команды осуществляется уточнение корня при использовании метода последовательных приближений? 3. В чем заключается отличие технологии нахождения корней нелинейных уравнений с помощью метода итераций от технологии нахождения корней нелинейных уравнений методом бисекции? 4. Укажите итерационную схему метода Ньютона. 5. Укажите специальные функции Excel для работы с матрицами. 6. Опишите технологию решения систем линейных алгебраических уравнений. 7. С помощью, какой сервисной программы Excel осуществляется решение систем нелинейных уравнений? 8. В чем заключается прямой и обратный ход методом Гаусса?
Практическая работа №5.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.123.103 (0.015 с.) |


 , (4.1)
, (4.1) ;
; 




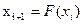 , (4.2)
, (4.2) (4.3)
(4.3) (4.4)
(4.4) .
. где
где
 (4.6)
(4.6)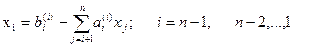

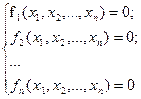 (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9)