
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если записать уравнение в видеСодержание книги
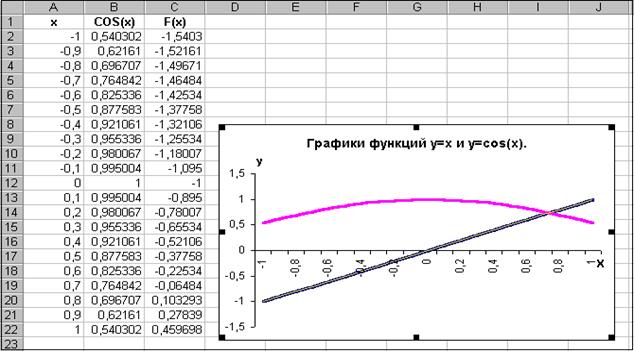
Поиск на нашем сайте f(x) =0 (3), то для применения этих алгоритмов нет необходимости накладывать какие-либо ограничения на функцию f(x), а предполагается только что она обладает некоторыми свойствами типа непрерывности, дифференцируемости и т.д. Эти свойства, накладываемые на функцию f(x) обусловлены теоремами о существовании корня непрерывной функции. Теорема 1. Если функция f(x) непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, то на этом отрезке существует, по крайней мере, один корень уравнения (3). Утверждение этой теоремы легко проиллюстрировать графически, так как корень уравнения (3) – это точка пересечения графика функции f(x) с осью абсцисс. Если же есть промежуток, на концах которого f(x) принимает значения разных знаков и функция непрерывна на этом промежутке, то, очевидно, существует, по крайней мере, одна точка, в которой график функции пересекает ось абсцисс. Теорема 2. Если функция f(x) непрерывна на отрезке [a, b], принимает на его концах значения разных знаков и производная функции f(x) сохраняет знак, то на этом отрезке существует корень уравнения (3), причем единственный. В качестве примера приложения этих теорем рассмотрим решение уравнения (2). Приведем его к виду (3): х–cos(x)=0, где f(x)=x–cos(x) Процесс нахождения приближённых значений корней уравнения разбивается на 2 этапа: 1) Отделение корней. 2) Уточнение корней до заданной степени точности. 1. Отделение корней. Будем считать, что корень уравнения отделен на отрезке [a, b], если установлено, что он принадлежит этому отрезку, и других корней там нет. Для решения данной задачи можно использовать программу Microsoft Excel. Вначале определим на каком отрезке лежит искомый корень. Для этого: 1. Включите компьютер; 2. после того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Excel; 3. сделаем первую строку – строкой заголовка, т.е. занесём в ячейкиA1, В1, С1 таблицы элементы х и cos(x) и F(x) соответственно; 4. активизируйте ячейку А2 и занесите в неё число –1, после чего нажмите на клавишу Enter; 5. в ячейке А3 запишите формулу: =А2+0,1, после чего автозаполнением заполните ячейки А4¸А22; 6. активизируйте ячейку В2 и запишите в неё формулу: =COS(A2), после чего нажмите на клавишу Enter; 7. автозаполнением заполните ячейки В3¸В22; 8. активизируйте ячейку С2 и запишите в неё формулу: =А2–COS(A2), после чего нажмите на клавишу Enter; 9. автозаполнением заполните ячейки С3¸С22. В результате мы получаем таблицу значений функции. Выберем промежуток, на котором функция меняет знак. Из рисунка 15.1 видно, что это отрезок [0,1].
Функция f(x)=x-cos(x) непрерывна на этом отрезке, при этом f(0)=-1, f(1)=0,4597, ее производная равна 2. Уточнение корня до заданной точности. Рассмотрим различные алгоритмы уточнения корня. Метод последовательных приближений.
Предположим. Что уравнение (3) можно записать в виде: x=j(x) (4) Возьмем произвольное значение х0 из области определения функции j(x) и будем строить последовательность чисел {xn}, определенных с помощью рекуррентной формулы xn+1=j(xn), n=0,1,2,…(5). Последовательность {xn}, называется итерационной последовательностью. При ее изучении возникают два вопроса: 1) Можно ли процесс вычисления чисел xn продолжать неограниченно, то есть, будут ли числа xn принадлежать области определения функции j(х)? 2) Если итерационный процесс бесконечен, то как ведут себя числа xn, при n ®¥? Исследование этих вопросов показывают, что при определенных ограничениях на функцию j(х) итерационная последовательность является бесконечной и сходится к корню уравнения (4):
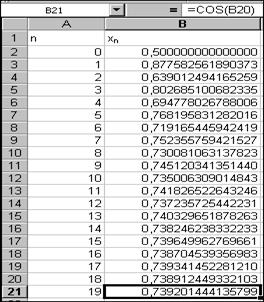
В качестве примера, иллюстрирующего данный метод, рассмотрим уравнение (2), в котором роль функции j(х) играет cos(x). Теперь, в соответствии с рекуррентной формулой (5) уравнение (2) перепишем следующим образом хn+1=cos(xn) (6). Корень этого уравнения будем искать на отрезке [0, 1], а в качестве нулевого приближения выбираем середину отрезка х0=0,5. В программе Excel расчет по (6) произведем для n=19. В этой таблице процесс вычислений остановлен на 19-ой итерации и можно написать для корня с двойное неравенство: 0,738912449332103< с <0,739201444135799, где х18=0,738912449332103, х19=0,739201444135799. Члены итерационной последовательности х18 и х19 определяют с как с недостатком, так и с избытком, с погрешностью, которая не превышает разности ½х19-х18½: e<D19=½х19-х18½<0,0003 Для иллюстрации зависимости поведения {xn} от n, построим график функции xn=xn(n) (см. рис. 15.2).
Рис. 15.2 Эта функция колеблется вокруг среднего значения с =
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.006 с.) |

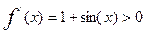 на всей области определения, следовательно, функция имеет единственный корень, который принадлежит отрезку [0, 1].
на всей области определения, следовательно, функция имеет единственный корень, который принадлежит отрезку [0, 1].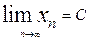 , C=j(C).
, C=j(C).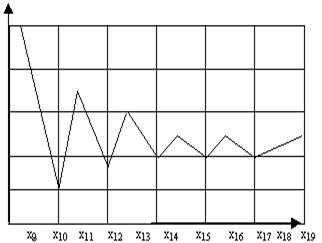
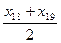 , которое можно принять за корень с точностью указанной погрешности.
, которое можно принять за корень с точностью указанной погрешности.


