
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Институт математики и информатикиСодержание книги
Поиск на нашем сайте Общеинститутская кафедра естественнонаучных дисциплин
Необходимый минимум баллов и форм работ для прохождения рубежной аттестации: 16 баллов (из них обязательные баллы: посещение занятий (п.1) не менее 4 баллов; выполнение лабораторных работ (п.2) не менее 6 баллов; выполнение домашних заданий (п.5) не менее 6 баллов). Необходимый минимум баллов и форм работ для допуска к промежуточной аттестации: 26 баллов (из них обязательные баллы: посещение занятий (п.1) не менее 6 баллов; выполнение лабораторных работ (п.2,3,4) не менее 10 баллов; выполнение домашних заданий (п.5,6) не менее 6 баллов, подготовка конспектов (п.7) не менее 4 баллов.
Студент, не выполнивший необходимый минимум работ, до сессии не допускается. ФИО преподавателя: доцент Селина Вера Олеговна Утверждено на заседании кафедры _____________________ от «___» _________ 201__ г. Протокол №__ Зав. кафедрой __________________ Приложение 1 Домашние задания Домашнее задание № 1. Определители.
Задача 1. Найти при каком значении параметра α определитель
Задача 2. Найти при каком значении α определитель
Задача 3. Найти при каком значении α определитель
Задача 4. Найти при каком значении α определитель
Задача 5. Найти при каком значении α определитель
Задача 6. Найти при каком значении α определитель
Задача 7. Найти при каком значении α определитель
Задача 8. Найти при каком значении α определитель
Задача 9. Найти значениеопределителя
Задача 10. Найти значение определителя
Задача 11. Найти значение определителя
Задача 12. Вычислить определитель
Задача 13. Вычислить определитель
Задача 14. Вычислить определитель
Задача 15. Вычислить определитель
Задача 16. Вычислить определитель
Задача 17. Вычислить определитель
Задача 18. Разложением по первой строке вычислить определитель
Задача 19. Разложением по первой строке вычислить определитель
Задача 20. Разложением по первой строке вычислить определитель
Задача 21. Разложением по первой строке вычислить определитель
Домашнее задание №2 Матрицы и операции над ними
Задача 1. Дана матрица
Найти сумму двух следующих ее элементов а11+ а32. Ответ: (- 7). Задача 2. Дана матрица найти сумму а12+ а23.
Ответ: (- 4). Задача 3. Найти сумму элементов, расположенных на главной диагонали.
Ответ: 15.
Задача 4. Найти сумму элементов, расположенных на второй диагонали.
Ответ: 9. Задача 5. Указать тип матрицы
Ответ: трапециевидная.
Задача 6. Указать тип матрицы
Ответ: единичная.
Задача 7. Указать тип матрицы
Ответ: верхняя.
Задача 8. Указать тип матрицы
Ответ: нижняя.
Задача 9. Указать тип матрицы
Ответ: симметричная.
Задача 10. Найти сумму двух следующих матриц
Ответ: Задача 11. Найти сумму двух следующих матриц
Ответ:
Задача 12. Найти сумму двух следующих матриц
Ответ:
Задача 13. Найти сумму двух следующих матриц
Ответ: Задача 14. Из матрицы А вычесть матрицу В:
Ответ:
Задача 15. Матрицу Ответ: λ• А=
Задача 16. Найти произведение А и В:
Ответ:
Задача 17. Найти произведение А и В:
Ответ: Задача 18. При каком значении параметра λ матрица
Ответ: λ = - 2
Задача 19. При каком значении параметра λ матрица
Задача 20. При каком значении параметра λ матрица
Задача 21. При каком значении параметра λ матрица
Задача 22. При каком значении параметра λ матрица
Задача 23. При каком значении параметра λ матрица
Ответ: λ = 2; Задача 24. Вычислить определители произведения матриц А и В
Ответ: Задача 25. Вычислить определители произведения матриц А и В
Ответ: Задача 26. Вычислить определители произведения матриц А и В
Ответ: Задача 27. Вычислить определители произведения матриц А и В
Ответ: Задача 28. Вычислить определители произведения матриц А и В
Ответ:
Задача 29. Найти ранг матрицы
Ответ: r = 1
Задача 30. Найти ранг матрицы
Ответ: r = 2
Задача 31. Найти ранг матрицы
Ответ: r = 2
Задача 32. Найти ранг матрицы
Ответ: r = 1
Задача 33. Найти ранг матрицы
Ответ: r = 2
Задача 34. При каком значении параметра λ матрица А не имеет обратной.
Ответ:
Задача 35. При каком значении параметра λ матрица А не имеет обратной.
Задача 36. При каком значении параметра λ матрица А не имеет обратной.
Задача 37. При каком значении параметра λ матрица А не имеет обратной.
Задача 38. При каком значении параметра λ матрица А не имеет обратной.
Задача 39. При каком значении параметра λ матрица А не имеет обратной.
Домашнее задание №3. Системы линейных алгебраических уравнений. Задача 1. Решить систему алгебраических уравнений
Задача 2. Решить систему алгебраических уравнений
Задача 3. Решить систему алгебраических уравнений
Задача 4. Решить систему алгебраических уравнений
Задача 5. Решить систему алгебраических уравнений
Задача 6. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 7. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 8. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 9. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 9. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ:
Задача 10. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 11. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 12. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 13. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 14. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 15. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 16. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 17. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 18. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 19. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 20. Представить в матричном виде системы линейных алгебраических уравнений
Ответ: Задача 21. Представить в матричном виде системы линейных алгебраических уравнений
Ответ: Задача 22. Представить в матричном виде системы линейных алгебраических уравнений
Ответ:
Задача 23. Представить в матричном виде системы линейных алгебраических уравнений
Ответ:
Задача 24. Представить в матричном виде системы линейных алгебраических уравнений
Ответ: Домашнее задание №4 Область определения. Частные производные. Производная по направлению. Градиент. Дифференциал.
Задача 1. Найти область определения функции 2-ух переменных
Ответ: I и III квадранты без границ. Задача 2. Найти область определения функции
Ответ: Вся плоскость, за исключением точек окружности Задача 3. Найти область определения функции
Ответ: I и III квадранты. Частные производные. Задача 1. Вычислить
Ответ: Задача 2. Вычислить
Ответ: Задача 3. Вычислить
Ответ: Производная по направлению. Задача 1. Вычислить производную функции
В точке Ответ: 7. Задача 2. Вычислить производную функции
В точке Ответ: Градиент. Задача 1. Найти градиент функции
Ответ: Задача 2. Найти градиент функции
Ответ: Задача 3. Найти градиент функции
Ответ: Дифференциал. Задача 1. Найти дифференциалы следующих функций 1) Ответ: 2) Ответ: 3) Ответ: Задача 2. Вычислить приближенное значениечислового выражения Домашнее задание №5. Производные и экстремумы функций.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |


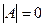
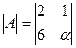 Ответ: α=3.
Ответ: α=3.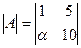 Ответ: α = 2;
Ответ: α = 2;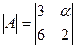 Ответ: α = 1;
Ответ: α = 1;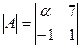 Ответ: α = - 7;
Ответ: α = - 7;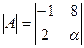 Ответ: α = -16;
Ответ: α = -16;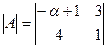 Ответ: α = - 11;
Ответ: α = - 11;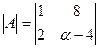 Ответ: α = 20;
Ответ: α = 20;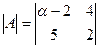 Ответ: α = 12
Ответ: α = 12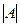 :
: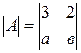 Ответ:
Ответ: 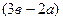
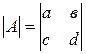 , Ответ:
, Ответ: 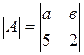 , Ответ:
, Ответ: 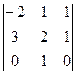 , Ответ:
, Ответ: 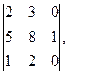 Ответ:
Ответ: 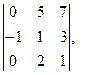 Ответ:
Ответ: 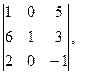 Ответ:
Ответ: 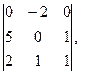 Ответ:
Ответ: 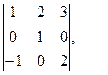 Ответ:
Ответ: 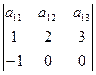 Ответ:
Ответ: 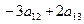
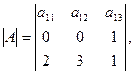 Ответ:
Ответ: 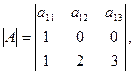 Ответ:
Ответ: 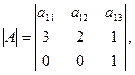 Ответ:
Ответ: 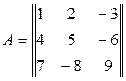
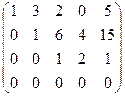
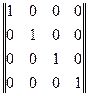
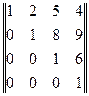
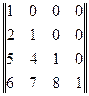
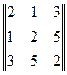

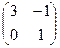
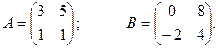
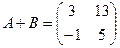 ;
;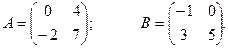
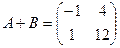 ;
;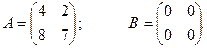
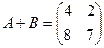
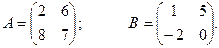
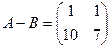 ;
;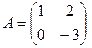 умножить на число λ=2.
умножить на число λ=2.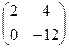 ;
;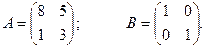
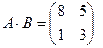 ;
;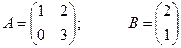
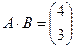
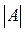 является вырожденной.
является вырожденной.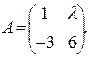
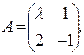 . Ответ: λ= -2;
. Ответ: λ= -2;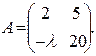 . Ответ: λ= - 8;
. Ответ: λ= - 8;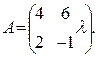 . Ответ: λ= 3;
. Ответ: λ= 3;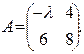 . Ответ: λ= - 3;
. Ответ: λ= - 3;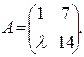 .
.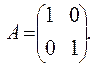 ,
, 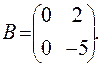 ,
,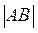 =0;
=0;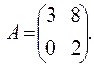 ,
, 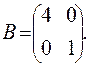 ,
,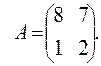 ,
, 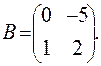 ,
,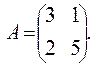 ,
, 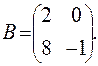 ,
,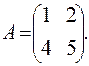 ,
, 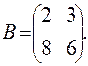 ,
,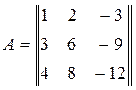
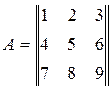
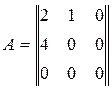
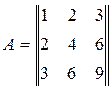
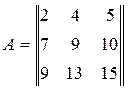
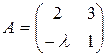
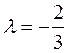
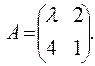 ,, Ответ:
,, Ответ: 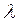 = 8;
= 8;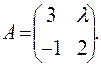 ,, Ответ:
,, Ответ: 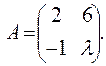 ,, Ответ:
,, Ответ: 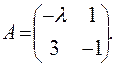 ,, Ответ:
,, Ответ: 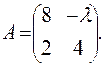 , Ответ:
, Ответ: 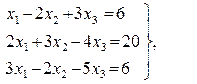 Ответ: х1 = 8, х2 = 4, х3 = 2;
Ответ: х1 = 8, х2 = 4, х3 = 2;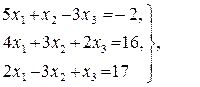 Ответ: х1 = 3, х2 = - 2, х3 = 5;
Ответ: х1 = 3, х2 = - 2, х3 = 5;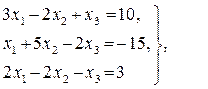 Ответ: х1 = 1, х2 = - 2, х3 = 3;
Ответ: х1 = 1, х2 = - 2, х3 = 3;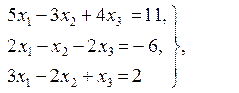 Ответ: х1 = 1, х2 = 2, х3 = 3;
Ответ: х1 = 1, х2 = 2, х3 = 3;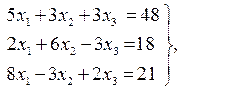 Ответ: х1 = 3, х2 = 5, х3 = 6
Ответ: х1 = 3, х2 = 5, х3 = 6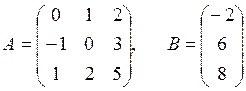
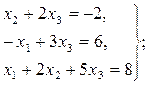
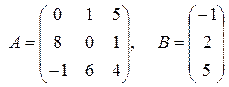
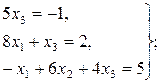
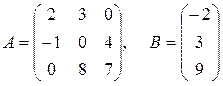
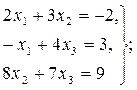
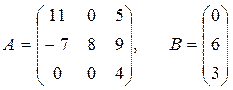
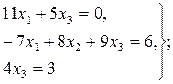
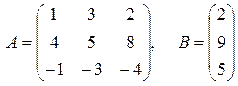
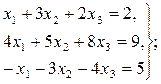

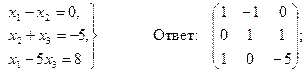

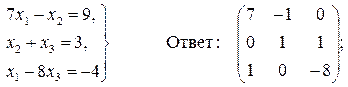
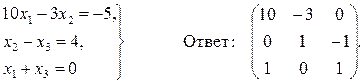
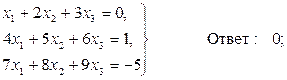
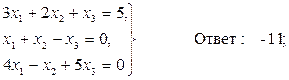
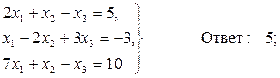
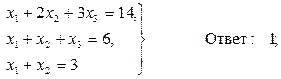
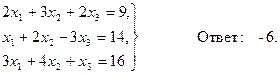
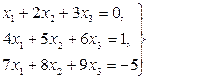
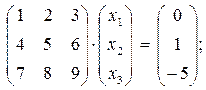
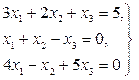
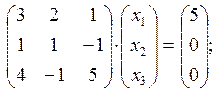
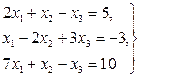
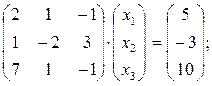
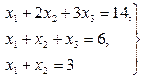
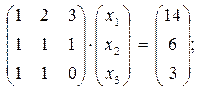
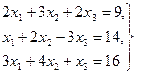

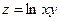
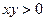
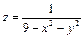
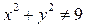
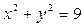
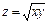
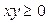
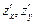
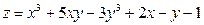
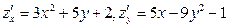
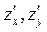
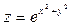
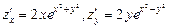
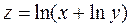
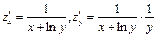
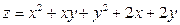
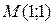 по направлению вектора
по направлению вектора 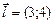
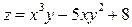
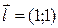
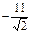
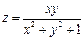 в точке
в точке 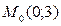
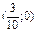
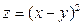 в точке
в точке 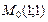
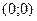
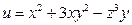 в точке
в точке 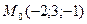
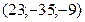
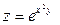
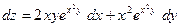
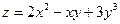
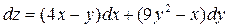
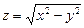
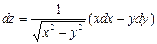
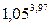 с помощью полного дифференциала 1-го порядка функции двух переменных
с помощью полного дифференциала 1-го порядка функции двух переменных


