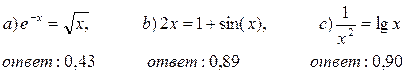Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уточнение корня методом половинного деления.Содержание книги
Поиск на нашем сайте Одним из вариантов метода проб является метод половинного деления. Он отличается тем, что на каждом следующем шаге отрезок делится не на 10 частей, а на две. При этом получается последовательность отрезков [a0,b0]; [a1,b1];…;[an,bn], удовлетворяющих условиям: f(ak)f(bk)<0 (k=0,1,2,3,…) bk-ak= ak<x*<bk (k=0,1,2,3,…) Процесс половинного деления прекращается в двух случаях: когда середина одного из полученных отрезков окажется корнем уравнения; когда получим отрезок, длина которого не превосходит заданной точности вычисления. Тогда за приближенное значение корня принимается число x*= Метод половинного деления не удобен для вычисления корня “безмашинным” способом, так как требуется выполнение большого объема вычислительной работы, но алгоритм решения этим методом очень прост и легко реализуется с помощью компьютера. Рассмотрим решение этим методом уравнения x-cos(x)=0
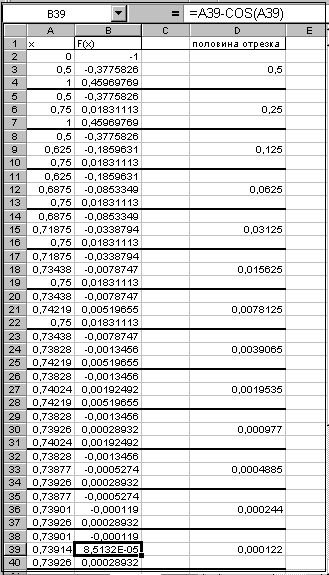
16. в ячейку А2 занесите число «0», а в ячейку А4 – 1; 17. активизируйте ячейку D3 и занесите в неё формулу: =(А4-А2)/2, после чего нажмите на клавишу Enter; 18. активизируйте ячейку А3 и вставьте в неё формулу: =А2+А3, после чего нажмите на клавишу Enter; 19. активизируйте ячейку В2 и запишите формулу: =А2-cos(А2), нажмите на клавишу Enter; 20. автозаполнением заполните ячейки А3¸А4. Таким способом будем продолжать процесс половинного деления, пока в ячейке В39 мы не обнаружим, что число бесконечно мало, т.е равно нулю 9см. рис. 15.5. Уточнение корня методом касательных (метод Ньютона).
y=f(x0)+f¢(x0)(x-x0) (7)

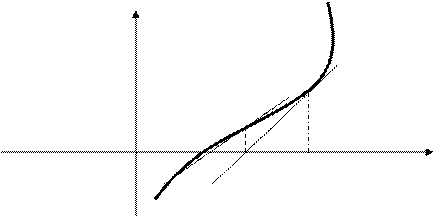
Найдем точку пересечения касательной с осью абсцисс – х1. Для определения координаты этой точки можем использовать уравнение f(x0)+f¢(x0)(x-x0)=0 Таким образом, x1=x0- Повторим проделанную процедуру: напишем уравнение касательной к графику функции в точке х1 и найдем точку пересечения этой касательной с осью Ох (см. рис.1): х2=x1- Продолжая этот процесс, получим последовательность {хn}, определенную с помощью рекуррентной формулы: xn+1=xn- При исследовании этой последовательности снова возникают два вопроса: 1) Можно ли процесс вычисления чисел xn продолжать неограниченно, иными словами, будут ли получившиеся значения принадлежать отрезку [a;b]? 2) Если процесс бесконечен, то как ведет себя последовательность {хn} при n®¥? Оказывается, что если значение х близко к искомому корню, то справедлива теорема о сходимости последовательности (9). Применим данный метод для решения уравнения (2). Итак, f(x)=x-cosx, рекуррентная формула имеет вид: xn+1=xn-
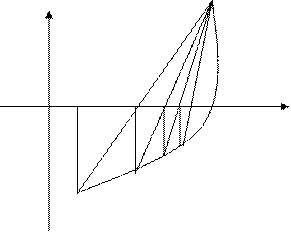
21. Активизруйте ячейку В14 и занесите в неё число 0,5; 22. в ячейке D14 запишите формулу: =В14-((B14-COS(B14))/(1+SIN(B14))), после чего нажмите на клавишу Enter; 23. в ячейку В15 занесите: =D14, и нажмите на Enter; 24. Результаты вычислений представлены на рис. 15.7 Из рисунка видно, что, начиная с номера n=1, последовательность {хn} убывает и приближается к корню х= с сверху. После четвертого шага процесс останавливается. Остановка связана с тем, что расчеты ведутся с 12 знаками, и после достижения погрешности, не превышающей 10-12, становится невозможно уловить разницу между xn+1 и xn, лежащую за пределами ошибки округления. 5. Уточнение корня методом хорд. Пусть корень уравнения (3) отделен на отрезке [a, b], функция f(x) – непрерывна на отрезке и принимает на его концах значения разных знаков. График функции y=f(x) проходит через точки A(a, f(a)) и B(b, f(b)). Запишем уравнение хорды АВ: Если у=0, то х=с1 – абсцисса точки пересечения хорды с осью Ох, может быть найдена по формуле: c1=a - Теперь возьмем на данной кривой точку А1(c1,f(c1))
y B
a=c0 c1 c2 b
A2 A1 A Рис. 15.8
Найдем абсциссу с2 точки пересечения хорды А1В с осью Ох
………………………… cn+1=cn - При возрастании числа n значение cn приближается к истинному значению корня. Этот процесс продолжается до тех пор, пока не получим приближенного значения корня с заданной точностью. Мы рассмотрели случай, когда «перемещается» левая граница отрезка [a, b]. Возможен и другой вариант, в этом случае формулы (11-12) имеют вид:
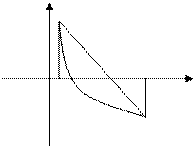
Возможны следующие четыре типа расположения дуги кривой АВ: 1. Функция убывает, график – вогнутая кривая
f¢(x)<0, f¢¢(x)>0
2. Функция убывает, график – выпуклая кривая
f¢(x)<0, f¢¢(x)<0
f¢(x)>0, f¢¢(x)>0
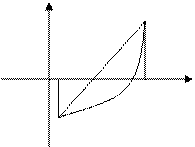
4. Функция возрастает, график – выпуклая кривая
f¢(x)>0, f¢¢(x)<0
Из рисунков видно, что формулы (11-12) применяются в случаях (2) и (3), то есть тогда, когда f¢(x)×f¢¢(x)<0, а формулы (13) применяются в случаях (1) и (4), то есть тогда, когда f¢(x)×f¢¢(x)>0. Методами математического анализа доказывается, что если f¢(x) и f¢¢(x) сохраняют знак на отрезке [a, b], то последовательность с1,с2,…cn,… сходится и ее предел равен истинному значению корня. Рассмотрим решение эти методом уравнения x-cosx=0. Корень уравнения x-cosx=0 будем искать на отрезке [0, 1] f¢(x)×=1+sin(x))>0, f¢¢(x)=cos(x))>0 на отрезке [0, 1], то есть имеет место (3) случай, поэтому применяем формулы (11-12), получаем:
Из таблицы видно, что, начиная с номера n=1, последовательность {сn} возрастает и приближается к корню х= с снизу. После пятого шага процесс останавливается. Остановка обусловлена теми же причинами, что и в предыдущем методе. Уточнение корня комбинированным методом хорд и касательных. Рассмотренные методы решения уравнений удобнее применять в сочетании друг с другом. Например, хороший результат дает комбинация методов хорд и касательных. При этом в случаях (1) и (4) метод хорд дает приближенное значение корня с избытком, а метод касательных – с недостатком, а в случаях (2) и (3) наоборот. Рассмотрим решение этим методом уравнения x-cos(x)=0. Корень уравнения x-cos(x)=0 будем искать на отрезке [0, 1]. Как сказано ранее, имеет место 3 случай, поэтому применяем формулы (11-12) и формулы (9). Получим
Рис. 15.9 Из таблицы видно, что результат достигается уже на третьем шаге.
Задания для самостоятельной работы. 1) Применяя метод проб, найдите корень уравнения с точностью до 0,1: х4 – 0,5х – 1=0. Ответ: -0,9; 1,2. 2) Применяя метод проб, найдите корень трансцендентного уравнения с двумя верными десятичными знаками:
3) Найдите корень уравнения комбинированным методом хорд и касательных с точностью до трёх десятичных знаков: a) x6+2x – 1=0 (положительный корень) ответ: 0,492 b) х2+lgx=5; ответ: 2,160 c) x+arctg x=10; ответ: 8,546 d) 3x+sin x=7. ответ: 2,035
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

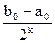 (k=0,1,2,3,…)
(k=0,1,2,3,…)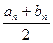 с погрешностью, не превышающей
с погрешностью, не превышающей 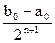 .
. Корень уравнения x-cos(x)=0 будем искать на отрезке [0, 1]
Корень уравнения x-cos(x)=0 будем искать на отрезке [0, 1] Метод касательных, связанный с именем И.Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f(x), имеющая корень на отрезке [a; b], дифференцируема на этом отрезке и ее производная f¢(x) не обращается на нем в нуль. Возьмем произвольную точку х0 проведем касательную к графику функции f(x) в этой точке и запишем уравнение касательной:
Метод касательных, связанный с именем И.Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f(x), имеющая корень на отрезке [a; b], дифференцируема на этом отрезке и ее производная f¢(x) не обращается на нем в нуль. Возьмем произвольную точку х0 проведем касательную к графику функции f(x) в этой точке и запишем уравнение касательной:
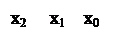
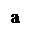
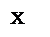
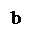

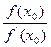 (8).
(8).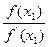
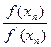 , n=0,1,2,… (9).
, n=0,1,2,… (9).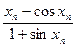 , n=0,1,2,… (10).
, n=0,1,2,… (10).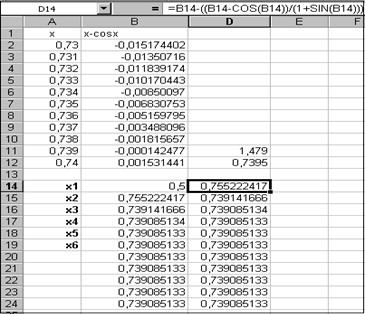 Выберем, как и ранее в качестве нулевого приближения х0=0,5 и вычислим несколько следующих приближений по формуле (10) с помощью программы Excel.
Выберем, как и ранее в качестве нулевого приближения х0=0,5 и вычислим несколько следующих приближений по формуле (10) с помощью программы Excel. автозаполнением заполните ячейки B16¸D24.
автозаполнением заполните ячейки B16¸D24.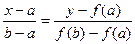
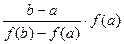 (11).
(11).
 с2=с1 -
с2=с1 - 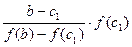
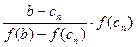
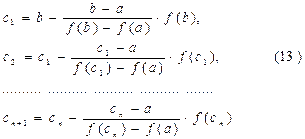
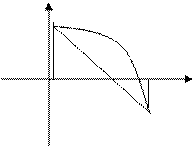
 3. Функция возрастает, график – вогнутая кривая
3. Функция возрастает, график – вогнутая кривая