Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №6. Вычисление ранга матрицы.Содержание книги
Поиск на нашем сайте
Рассмотрим матрицу типа [ n ´ m ]:
Если в этой матрице выделить произвольно k столбцов и k строк, то элементы, стоящие на пересечении выделенных столбцов и строк, образуют квадратную матрицу k -го порядка. Определитель этой матрицы называется минором k -го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдётся, по крайней мере, один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если все элементы матрицы А равны нулю, то говорят, что ранг матрицы А равен нулю. Если ранг матрицы А равен r, то это означает, что в матрице А имеется, по крайней мере, один, отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(А). Очевидно, что всегда выполняется соотношение 0 £ r £ min (m,n). Свойство 1. При транспонировании матрицы её ранг не меняется. Свойство 2. Ранг матрицы не меняется при перестановке её столбцов (строк). Свойство 3. Ранг матрицы не меняется при умножении всех элементов её столбца (строки) на отличное от нуля число. Свойство 4. Ранг матрицы не изменится, если к одному из её столбцов (строк) прибавить другой столбец (строку), умножив его (её) на некоторое число. Свойство 5. Ранг матрицы не изменится, если удалить из неё столбец (строку), состоящий из одних нулей. Свойство 6. Ранг матрицы не изменится, если удалить из неё столбец (строку), являющийся линейной комбинацией других столбцов (строк). Элементарными называются следующие преобразования матриц: 1) перестановка двух любых столбцов (строк); 2) умножение столбца (строки) на отличное от нуля число; 3) прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк). Из перечисленных выше свойств ранга матрицы следует, что при элементарных преобразованиях матрицы её ранг не меняется. Две матрицы называют эквивалентными, если одна из них получается из другой с помощью применения конечного множества элементарных преобразований. Эквивалентные матрицы не являются равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А~В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например:
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на её главной диагонали. На практике для вычисления ранга матрицы достаточно привести матрицу к ступенчатому виду. Пусть нам дана матрица А, имеющая следующий вид:
Чтобы вычислить ранг матрицы А, необходимо с помощью элементарных преобразований, преобразовать её к такому виду, в котором все элементы, располагающиеся ниже главной диагонали, были равны нулю. Для этого произведём анализ строк матрицы А. Интерес вызывает 2-я строка, в которой 1-й элементы равен 1, следовательно, используя свойства 1-4, во всех строках, кроме этой, получить ряд нулевых элементов с помощью следующих преобразований над строками: - к элементам 1-ой строки прибавим элементы 2-ой, умноженные на (-2); - к элементам 3-ей строки прибавим элементы 2-ой, умноженные на (-2); - к элементам 4-ой строки прибавим элементы 2-ой, умноженные на (-3). В результате получим матрицу Ā~А:
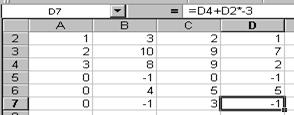
где вторая строка матрицы А становится первой строкой в матрице Ā. В качестве вычислительного средства воспользуемся инструментами программы Excel. Для этого: 1. Включите компьютер. 2. После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно MicrosoftExcel. 3. Заполните ячейки таблицы значениями матрицы А (рис. 6.1). После появления на экране компьютера матрицы А осуществляется указанный выше анализ строк. Для выполнения выбранного словесного алгоритма производим следующие действия. · Активизируйте ячейку А5 и занесите в неё с клавиатуры формулу =А1+А2*(-2). Результат занесите автозаполнением в ячейки В5¸D5. ·В ячейке А6 разместите результат прибавления к 3-ей строке 2-ой, умноженной на (-2). Результат, полученный в ячейке, автозаполнением занесите в ячейки В6¸D6. ·В ячейке А7 запишем формулу =А4+А2*(-3), после чего автозаполнением заполните ячейки В7¸D7 (см. рис. 6.2).
Рис. 6.1 Рис. 6.2 Из рис.38 видно, что в результате проделанных вычислений строки матрицы Ā оказались в ячейках А2¸D2, А5¸D5, А6¸D6, А7¸D7.
4. Снова глядя на экран компьютера, анализируем строки и составляем следующий словесный алгоритм, позволяющий преобразовать матрицу Ā так, чтобы в ней появились нулевые элементы ниже главной диагонали: - прибавим к 3-ей строке 2-ю, умноженную на число 4; - прибавим к элементам 4-ой строки элементы 2-ой, умноженные на число (-1). В результате получим новую матрицу В~Ā:
Реализация этого словесного алгоритма производится следующим образом. · Активизируем ячейку А8 и запишем в неё формулу =А6+А5*4 и затем численный результат, полученный в ней, заносим автозаполнением в ячейки А7¸D7. ·В ячейке А9 разместим результат прибавления 5-ой строки, умноженной на число (-1), к 7-ой, после чего автозаполнением занесём численные результаты в ячейки А9¸D9. 5. Анализируя строки полученной матрицы составляем следующий словесный алгоритм, позволяющий окончательно преобразовать матрицу В~ В /. Для этого: ·прибавим к 3-ей строке матрицы В 4-ю строку, умноженную на число (-5) и деленную на число 3. Матрица В / ~А, будет иметь следующий вид:
· 6. Элементы преобразованной матрицы В / находятся в строках 2, 5, 9 и 10. Для того, чтобы все другие строки не мешали подсчёту ранга матрицы В /, воспользуемся пунктом меню ФОРМАТ и скроем их. Для этого: ·
 , выполните нажатие ЛКМ на ячейке А3 и протащите его до ячейки D4; , выполните нажатие ЛКМ на ячейке А3 и протащите его до ячейки D4;
· ·
После проделанных действий на экране монитора возникнет следующее изображение (рис. 6.5). & Далее, в тексте задачника будем обозначать: скройте строки... Аналогичным способом скройте строки 1, 6, 7, 8. Экран программы Excel примет вид (рис. 6.6).
Рис. 6.5 Рис. 6.6 С помощью элементарных преобразований над строками матрицы А мы получили матрицу В /, эквивалентную матрице А. При этом r(В / )= r(А) = 4 Задания для самостоятельной работы.
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.105 (0.01 с.) |



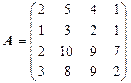
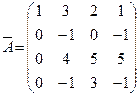


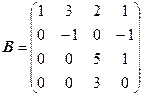

 Активизируем ячейку А10 и запишем в неё формулу =А8+А9*(-5)/3 и затем численный результат, полученный в ней, заносим автозаполнением в ячейки А10¸D10, см. рис. 6.3.
Активизируем ячейку А10 и запишем в неё формулу =А8+А9*(-5)/3 и затем численный результат, полученный в ней, заносим автозаполнением в ячейки А10¸D10, см. рис. 6.3. отпустите кнопку мыши при этом диапазон ячеек А3÷D4, окажется выделенным другим цветом;
отпустите кнопку мыши при этом диапазон ячеек А3÷D4, окажется выделенным другим цветом;