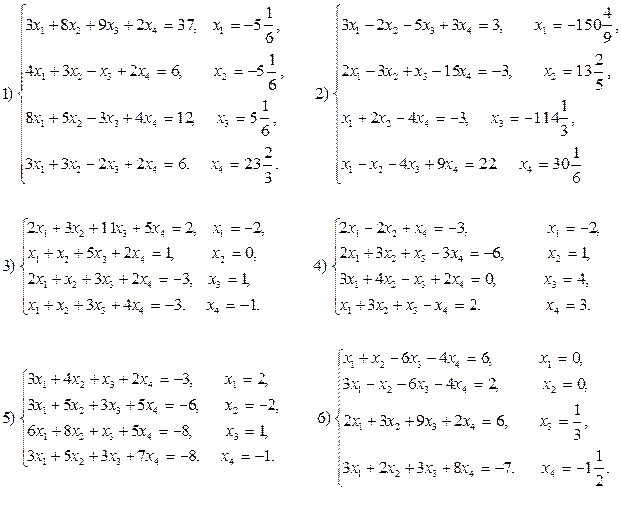Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №9. Решение систем линейных уравнений по формуле Крамера.Содержание книги
Поиск на нашем сайте
Пусть дана система n -линейных уравнений с n- неизвестными х1, х2,..., х n:
............................... аn 1х1+ аn 2х2+...+ аnnхn = bn. Матрица, составленная из коэффициентов при неизвестных, и её определитель называются соответственно матрицей системы (1) и определителем этой системы.
Dх2= b 1А12+ b 2 А22+...+ bn А n 2, ......................................., Dх n = b 1А1 n + b 2 А2 n +...+ bn А nn. Правые части уравнения системы (2) обозначим соответственно символами D1, D2,..., Dn, где
Тогда система уравнений (2)примет вид:
Dх2=D2, ............, Dх n =D n. Если D¹0, то из этих уравнений находим
Полученные формулы называются формулами Крамера; они дают решение системы (2), полученной из системы (1). Формулы Крамера (5) являются единственным решением системы (1), поскольку система (2) выведена из системы (1). Таким образом, следует Теорема: если определитель системы (1) отличен от нуля, то система имеет единственное решение, получаемое по формулам Крамера. Правило Крамера. Система n уравнений с n переменными, определитель которой отличен от нуля, всегда имеет решение и притом единственное, определяемое следующим правилом: значение каждого из переменных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом переменном столбцом свободных членов. Решим следующую систему уравнений с 4-мя неизвестными:
х1+3х2+2х3+х4=11, 2х1+10х2+9х3+7х4=40, 3х1+8х2+9х3+2х4=37. Определитель матрицы, составленный из коэффициентов при неизвестных данной системы D= -3, отличен от нуля, поэтому к системе применимо правило Крамера. Используя редактор формул, запишем определители D1, D2, D3 и D4, используя формулу (3).
Для этого: 1. Включите компьютер. 2. 3. Вставьте объект Microsoft Equation 3. 0. 4. Запишем определитель D1 в формульный редактор. Для этого: ·
 ; ;
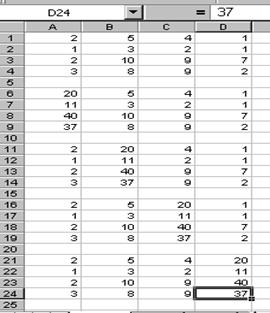
· вставьте шаблон определителя 4-го порядка в формульном редакторе; · занесите числовые значения определителя в свободные поля; Повтором предыдущих действий, запишите в редакторе формул определители D2¸D4 (см. рис. 9.1) В качестве вычислительного средства воспользуемся инструментами программы Excel– 97. 5. Откройте окно MicrosoftExcel. 6. Перепишите определители D, D1, D2, D3 и D4, из Word в Excel (см. рис. 9.2).
Рис. 9.2 Рис. 9.3 7. Используя функцию МОПРЕД, которая находится в мастере функций ƒх на стандартной панели, найдите, чему будут равны все пять определителей (см. рис. 9.3) Получаем, что D= -3, D1= -3, D2= -6, D3= -6 и D4= -1,11Е-14. Так как результат вычислений определителя D4 записан в виде числа с мантиссой, следовательно, поменяем формат ячейки Е25 на ДРОБНЫЙ, после чего определитель D4 станет равным нулю. 8. Найдём неизвестные х1, х2, х3, х4. Для этого: · активизируйте ячейку G10 и запишите в не формулу: · активизируйте ячейку G15 и запишите в не формулу: · активизируйте ячейку G20 и запишите в не формулу: · активизируйте ячейку G25 и запишите в не формулу: Задания для самостоятельной работы.
Пользуясь методом Крамера, решить следующие системы уравнений:
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.42.59 (0.05 с.) |

 а 11х1+ а 12х2+...+ а 1 nхn = b 1,
а 11х1+ а 12х2+...+ а 1 nхn = b 1,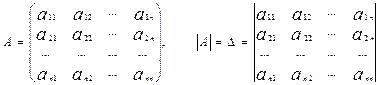
 Пусть А ij (i, j = 1, 2,..., n)– алгебраические дополнения элементов определителя D. Преобразуем систему (1) так, чтобы каждое из её уравнений содержало только одно неизвестное. Для этого умножим первое уравнение системы на А11, второе – на А21,..., n -е – на А n 1 и сложим их; затем умножим уравнения системы соответственно на А21, А22,..., А n 2 и сложим их, и т.д., наконец, умножим уравнения системы соответственно на А n 1, А n 2,..., А nn и опять сложим. Получим новую систему уравнений:
Пусть А ij (i, j = 1, 2,..., n)– алгебраические дополнения элементов определителя D. Преобразуем систему (1) так, чтобы каждое из её уравнений содержало только одно неизвестное. Для этого умножим первое уравнение системы на А11, второе – на А21,..., n -е – на А n 1 и сложим их; затем умножим уравнения системы соответственно на А21, А22,..., А n 2 и сложим их, и т.д., наконец, умножим уравнения системы соответственно на А n 1, А n 2,..., А nn и опять сложим. Получим новую систему уравнений:


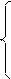 2х1+5х2+4х3+х4=20,
2х1+5х2+4х3+х4=20,
 После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Word.
После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Word.
 , после чего нажмите на клавишу Enter. В результате получим х1=1;
, после чего нажмите на клавишу Enter. В результате получим х1=1; , после чего нажмите на клавишу Enter. В результате получим х2=2;
, после чего нажмите на клавишу Enter. В результате получим х2=2; , после чего нажмите на клавишу Enter. В результате получим х3=2;
, после чего нажмите на клавишу Enter. В результате получим х3=2; , после чего нажмите на клавишу Enter. В результате получим х4=0.
, после чего нажмите на клавишу Enter. В результате получим х4=0.