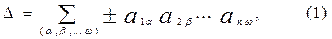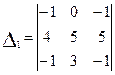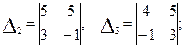Лабораторная работа №5 . Словесные алгоритмы линейной алгебры и их реализация в программе Excel.

В большинстве математических задач ответ даётся в виде формулы. Формула определяет последовательность математических операций, которую нужно выполнить для вычисления искомой величины.

Однако известны задачи, для которых ответ легко может быть найден, хотя он и не записывается в виде формулы. Например, можно ли назвать формулой правило вычисления суммы нескольких чисел с помощью поразрядного сложения столбиком? В то же самое время это правило полностью решает поставленную задачу: оно определяет последовательность математических операций, которую нужно выполнить для вычисления искомой величины.

Итак, для решения математической задачи важно указать систему правил, которая задаёт строго определённую последовательность математических операций, приводящих к искомому ответу. Такую систему правил называют алгоритмом. Формульные алгоритмы легко программируются традиционными языками программирования и их ещё называют вычислительными алгоритмами.

В качестве примера не формульного алгоритма можно указать на метод отыскания наибольшего общего делителя двух целых чисел. Этот метод состоит в поэтапном представлении большего числа в виде суммы из двух слагаемых. Одно слагаемое представляет произведение числа на частное от деления большего числа на меньшее, а другое – остаток указанного деления. Процесс поэтапного представления заканчивается, когда остаток становиться равным нулю. Этот метод называют алгоритмом Евклида.

Отличие такого алгоритма от формульного состоит в том, что он требует дополнительных логических операций, чтобы вычислительный процесс для любых двух чисел вести по данной системе правил. Например, в данном случае необходимо определить – какое из данных двух чисел представляется большим.

Если указанных дополнительных операций много в данной системе правил, то программирование таких алгоритмов традиционными языками программирования затруднено из-за ограниченности логических операций в языке программирования.

Чтобы различать такие алгоритмы от формульных, назовем их словесными алгоритмами.

Словесные алгоритмы могут представляться и некоторыми приемами упрощения формульных алгоритмов с целью сокращения числа арифметических операций.

Действительно, рассмотрим алгоритмы вычисления определителей в линейной алгебре. Пусть дана квадратная матрица А n -го порядка: ||A|| = a_ij (i=1,2,3..n; j=1,2,3..n). Тогда по определению, определителем матрицы А п -го порядка называется сумма всех п! произведений элементов этой матрицы, взятых по одному из каждой строки и по одному из каждого столбца; при этом каждое произведение снабжено знаком плюс или минус по некоторому правилу.

В соответствии с данным определением величину определителя следует вычислять по формуле

где суммирование ведётся по всем п! перестановкам (a,b,...w) из чисел 1, 2,... п. Знак перед каждым произведением в (1) определяется по общеизвестному правилу, которое не влияет на количество выполняемых арифметических операций.

Вычисление определителя п -го порядка по формуле (1) представляет весьма трудоёмкий процесс, так как число слагаемых, из которых составляется определитель, очень быстро растёт с увеличением п. Например, если п =20, то требуется выполнить 19·20!»4,5·10¹⁹ умножений. На машине, которая делает миллион умножений в секунду, такой расчёт продолжался бы 1,4·10⁶ лет.

Поэтому существует вычислимый алгоритм, основанный, например, на формуле разложения определителя по элементам любой строки. Эта формула для определителя п -го порядка имеет вид:

D = а_{i 1} A _{i 1} + a_{i 2} A _{i 2} + … + a_in A _in (2).

Учитывая связь между алгебраическими дополнениями и минорами:

A _ij = (-1) ^i+j M _{ij ,}

можно записать:

D = а_{i 1} (-1) ^{i+ 1} M _{i 1} + a_{i 2} (-1) ^{i+ 2} M _{i 2}+ … + a_in (-1) ^i+п M _iп (3).

С помощью этой формулы вычисление определителя п -го порядка D сводится к вычислению ряда определителей (п - 1)-го порядка - миноров M _{i 1,} … M _iп. Каждый из этих определителей, в свою очередь, можно свести к определителям (п - 2)-го порядка, эти последние - к определителям порядка п - 3 и т.д. В конечном счёте, вычисление D может быть сведено к вычислению определителей только 2-го порядка.

В вычислительный процесс, определяемый формулами (2)-(3), входит и словесный алгоритм вычисления определителя п -го порядка и миноров как определителей (п -1)-го порядка. Этот словесный алгоритм диктуется следующим определением: минор М _ij элемента а_ij матрицы А п -го порядка есть определитель матрицы (п -1)-го порядка, полученной вычёркиванием в матрице А i -ой строки и j -го столбца и сдвигом оставшихся элементов без нарушения их порядка.

Для уменьшения числа арифметических операций в формуле (3) можно с помощью элементарных преобразований над строками или столбцами исходного определителя преобразовать его к такому виду, в котором в i -ой строке будет как можно больше нулевых элементов. В частности, когда в i -ой строке только элемент а_ij ¹0, то формула (3) упрощается так:

D = а _ij (-1) ^i+j M _ij (4).

Элементарные преобразования над строками или столбцами определителя представляются словесными алгоритмами, основанными на следующих свойствах определителей.

Свойство 1. Если поменять местами две строки или столбца, определитель изменит знак.

Свойство 2. Определитель матрицы п -го порядка не изменится, если к элементам одной его строки прибавить соответствующие элементы другой строки, умноженные на одно и то же произвольное число. То же самое справедливо и для столбцов.

К сожалению, словесные алгоритмы не инвариантны. Они зависят от конкретного вида определителя и в пределах одного определителя, как правило, неоднозначны, т.е. различными преобразованиями можно получить одну и ту же форму определителя.

Именно поэтому реализацию словесных алгоритмов удобно осуществлять в программе Excel.

Ранее было введено понятие входной язык программы и приведены примеры программ на указанном языке. Оказалось, что процесс программирования на входном языке сводится к построению различных технологий пользования главным меню программы применительно к поставленной задаче.

Проиллюстрируем процесс программирования в Excel словесных алгоритмов линейной алгебры, необходимых для вычисления по формулам (3)-(4) следующего определителя:

Чтобы вычислить данный определитель по формуле (4), необходимо с помощью элементарных преобразований преобразовать его к такому виду, в котором в любой из строк содержался только один элемент не равный нулю. Для этого произведём анализ строк определителя D. Интерес вызывает 2-я строка, в которой 1-й элементы равен 1, следовательно, в этой строке можно получить ряд нулевых элементов с помощью следующих преобразований над столбцами:

- к элементам 2-го столбца прибавим элементы 1-го, умноженные на (-3);

- к элементам 3-го столбца прибавим элементы 1-го, умноженные на (-2);

- к элементам 4-го столбца прибавим элементы 1-го, умноженные на (-1).

В результате в соответствии с формулой (4) будем иметь

D= (-1) · D₁ (5),

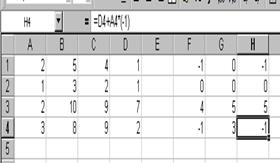
где

В качестве вычислительного средства воспользуемся инструментами программы Excel– 97.

1. Включите компьютер.

2. Подождите пока загрузится операционная система Windows, после чего откройте окно MicrosoftExcel.

3. Заполните ячейки таблицы значениями определителя D (рис. 5.1).

После появления на экране компьютера матрицы А осуществляется указанный выше анализ строк. Для выполнения выбранного словесного алгоритма производим следующие действия.

· Активизируйте ячейку F1 и занесите в неё с клавиатуры формулу =В1+А1*(-3). Результат занесите автозаполнением в ячейки F2¸F4.

· В ячейке G1 разместите результат прибавления к 3-му столбцу 1-го, умноженного на (-2). Результат, полученный в ячейке, автозаполнением занесите в ячейки G2¸G4.

· В ячейке Н1 запишем формулу =D1+А1*(-1), после чего автозаполнением заполните ячейки Н2¸Н4 (см. рис. 5.2).

Рис.35

Рис. 5.1 Рис. 5.2

Из рис.36 видно, что в результате проделанных вычислений столбцы определителя D₁ оказались в ячейках F1, F3, F4; G1, G3, G4; H1, Н3, H4.

Теперь в соответствии с формулой (3) определитель D₁ разложим по элементам 1-ой строки. Тогда будем иметь:

D₁= (-1) D₂ + (-1) D₃ (6).

При этом определители D₂ и D₃ имеют вид:

а их элементы оказались в ячейках: G3, G4, Н3, H4 (для D₂); F3, F4, G3, G4 (для D₃).

Для вычисления определителей 2-го порядка D₂ и D₃ в строку формул рабочего листа Excel необходимо последовательно ввести следующие формулы в ячейки Н5 и I5:

 

После последовательного вычисления по этим формулам получим: D₂= 20 (ячейка Н5); D₃= -17 (ячейка I5).

Возвращаемся снова к строке формул и заносим там выражение для вычисления формулы (6):

Вычисление по (6) дает D₁= 3 (ячейка J5 рабочего листа Excel).

Наконец вычисляем по формуле (5) искомый определитель D:

в результате будем иметь D=-3.

Таким образом, указан вычислимый алгоритм, который применим к любому определителю любого порядка. Если исходный определитель высокого порядка, то процесс его вычисления не обязательно доводить до вычисления определителей 2-го порядка. Можно остановиться на определителе более низкого порядка по сравнению с исходным, который в дальнейшем вычислить с использованием меню МАСТЕР ФУНКЦИЙ.

Предложенный вычислимый алгоритм представляет комбинацию словесных и формульных алгоритмов. Он легко программируется на входном языке Excel и программа на этом языке отлаживается одновременно с вычислениями благодаря взаимодействию пользователя с компьютером.

 

Задания для самостоятельной работы.

Посчитайте определители следующих матриц: