Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 2. Изучение числовых последовательностейСодержание книги
Поиск на нашем сайте
Для выполнения данной лабораторной работы необходимо знать определение последовательности, предела последовательности, возрастающей и убывающей последовательности, поэтому напомним некоторые понятия теории последовательностей. Если каждому числу п натурального ряда чисел 1, 2,..., n,... ставится в соответствие по определенному закону некоторое действительное число
называется числовой последовательностью или просто последовательностью. Числа -х„ называются элементами или членами последовательности (1). Сокращенно последовательность (1) обозначается символом { хn } (или (xn)). Наиболее распространенные способы задания последовательностей аналитический и рекуррентный. Аналитический - это способ задания с помощью формулы п -го («общего») члена an=f(n). Рекуррентный, когда любой член последовательности, начиная с некоторого, выражается через предшествующие (один или несколько). При этом способе задания указывается первый член последовательности (или несколько первых членов) и формула, позволяющая определить любой член последовательности по известным предшествующим членам. Последовательность (аn) называется убывающей (невозрастающей), если Число а называется пределом последовательности (аn), если для любого положительного числа То же определение коротко можно сформулировать так: Число а есть предел последовательности (аn), если ее значения отличаются от а сколь угодно мало, начиная с некоторого места. Последовательность, имеющую предел Постановка задачи. С помощью табличного процессора MS Excel 2000 найти двадцать первых членов последовательностей, если известно, что
Выяснить вопрос о возрастании (убывании) и пределе последовательностей. Для решения поставленной задачи придется несколько раз выполнять одни и теже операции для разных последовательностей. Поэтому целесообразно создать макросы для облегчения работы. Макрос - набор инструкций, указывающих последовательность действий, которые должен выполнить Microsoft Excel. Макрос - это, по сути дела, программа, предназначенная для решения некоторой специфической задачи и выполняющейся только внутри Excel. Ход работы: 1. Включите компьютер. 2. Щелкните на кнопке 3. Выберите команду Программы → Microsoft Excel. Программа Excel откроет новый документ (рабочую книгу).
4. Создайте файл, в котором будут храниться результаты вашей работы. Для этогонужновыбрать команду Файл → Сохранить как (рис. 1). В открывшемся диалоговом окне Имя файла выделенное имя Книга1 удалить нажатием клавиши
Рис. 1 Delete, после чего набрать с клавиатуры необходимое имя (например, Последовательности_1), а в строке Папка выбрать двойным щелчком имя нужной папки (например, Воробьев). Щелкнуть на кнопке " Сохранить " в окне диалога 5. Чтобы избежать потери данных регулярно сохраняйте рабочий материал с помощью команды Файл → Сохранить или щелчка мышью на кнопке Сохранить
6. На открывшемся Листе1 запишите общий член последовательности (1), вычислите 20 первых членов последовательности (1) и разности между членами последовательности и предыдущими членами. Для этого выполните следующие действия: 1) начните запись Макроса1, который будет создан для заполнения соответствующих ячеек текстовой информации и номерами членов последовательностей, с этой целью: а) выполните команду Сервис → Макрос → Начать запись (рис. 2);
Рис. 2
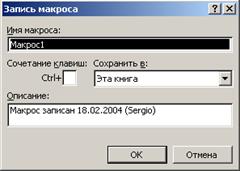
b) в открывшемся диалоговом окне Запись макроса в поле Имя макроса появится заданное по умолчанию название Макрос1 (рис. 3);
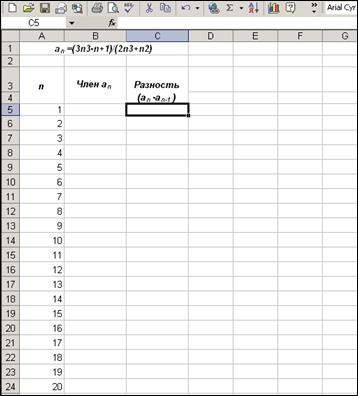
Рис. 3 c) чтобы сохранить Макрос1 в активной книге, убедитесь, что в поле Сохранить в выводится Эта книга; d) щелкните на кнопке ОК. В рабочем окне Excel появится панель инструментов Остановка записи e) чтобы панель не мешала вашим дальнейшим действиям, перенесите ее вправо, ухватившись за рамку, расположенную в верхней части панели; 2) осуществите запись Макроса1 (рис. 4):
Рис. 4
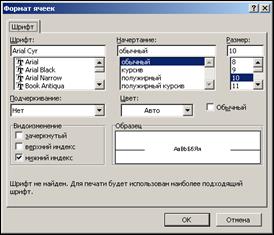
а) в ячейку А1 введите текст "аn=", для этого текст "аn=" наберите на латинском языке. На латинский язык с русского, и наоборот, можно переключиться с помощью нажатия клавиш Shift + Ctrl. Затем выделите с помощью мыши букву n (это можно сделать как в активной ячейке, так и в строке формул, расположенной в верхней части экрана) и выполните команду Формат → Ячейки. В диалоговом окне Формат ячеек установите флажок Нижний индекс (рис. 5). Щелкните на кнопке ОК. Рис. 5
Нижний индекс будет отображен только в активной ячейке, ноне в строке формул. Нажмите Enter; b) выделите диапазон ячеек А1:С1 и объедините его с помощью кнопки c) выделите ячейки A3, А4 и объедините их (кнопка d) измените ширину и высоту ячейки ВЗ. Для этого выберите команду Формат → Строка → Высота (рис. 6). В диалоговом окне Высота строки
Рис. 6
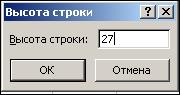
замените 12,75 на 27 и щелкните на кнопке ОК. Для этого нажмите, а затем с клавиатуры наберите 27 (рис. 7).
Рис. 7.
Далее выберите команду Формат → Столбец → Ширина. В диалоговом окне Ширина столбца 8,4 замените на 12, как было сказано в этом пункте выше; e) введите в ячейку ВЗ текст "Член an", an введите также как и в п°а). При выделении n, пусть вас не смущает, то, что выделяется все оставшееся поле ячейки после n. В строке формул поместите курсор после символа n. Нажмите левый Alt + Enter, чтобы поднять текст внутри ячейки, а затем Enter; f) выделите ячейки ВЗ, В4 и объедините их (кнопка g) измените ширину ячейки СЗ на 12 (как было описано в пункте 6.2.d); h) введите в ячейку СЗ текст "Разность (an-an-1)". После ввода слова "Разность" нажмите левый Alt + Enter, чтобы текст перешел на другую строчку внутри ячейки; i) выделите ячейки СЗ, С4 и объедините их (кнопка j) выделите диапазон ячеек АЗ:С4 с помощью мыши, щелкните последовательно на кнопках k) в ячейку А5 введите 1;
l) в ячейку А6 введите 2; m) выделите ячейки А5 и А6 и протяните их до ячейки, схватившись за маркер автозаполнения, расположенный в нижнем правом углу выделенного диапазона (значок +). Столбец окажется заполненным первыми двадцатью числами натурального ряда; n) активизируйте ячейку А1; o) щелкните на кнопке 3) в ячейку А1 введите дополнительно (3n3-n+1)/(2n3+n). (см. рис.2).С этойцелью введите с клавиатуры (3n3-n+l)/(2n3+n). Выделите 3, которая должна стать степенью, затем выполните команду Формат → Ячейки, в диалоговом окне Формат ячеек установите флажок Верхний индекс. Аналогично вводятся и остальные степени. Нажмите Enter; 4) в ячейку В5 введите формулу первого члена ряда =(3*A5^3-A5+1)/(2*A5^3+A5)(рис. 8). Нажмите Enter. В ячейке В5 отобразится е сама введенная формула, а вычисленное по ней значение. Тем не менее, на самом деле в ячейке содержится формула, которая и отображается в строке формул;
Рис. 8. 5) выделите ячейку В5 и с помощью автозаполнения заполните ячейки В6:В24. Благодаря относительным ссылкам на ячейки в ячейку В6 запишется формула =(3*A6^3-A6+l)/(2*A6^3+A6), в ячейку В7 формула: =(3*A7^3-A7+1)/(2*A7^3+A7) и т.д. Адреса ячеек в формуле можно вводить или с клавиатуры или с помощью "щелчка" мышью на требуемой ячейке; 6) на основании полученных данных столбца В сделайте вывод о существовании предела последовательности (1). Введите в ячейку D1 слово "сходится", если последовательность имеет конечный предел, и "расходится" в противном случае. Объедините ячейки, как было показано в п°2.b); 7) в ячейку С6 введите формулу =В6-В5;
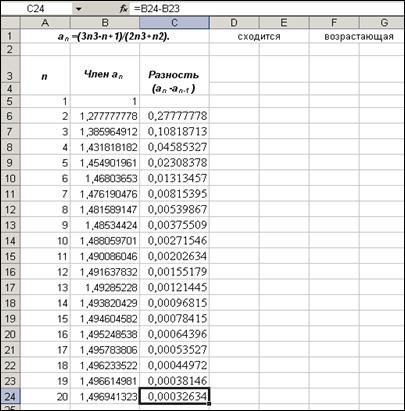
8) выделите ячейку С6 и с помощью автозаполнения заполните ячейки С7:С24 (Рис. 9.); Рис. 9.
9) на основании полученных данных столбца сделайте вывод о возрастании (убывании) последовательности (1). Введите в ячейку Е1 необходимую информацию: возрастающая, убывающая или не возрастающая и не убывающая (рис. 9); 10) чтобы подтвердить вывод, сделанный в пункте 6, нужно выяснить поведение последовательности при достаточно больших п. Для этого произведите следующие действия:
а) выделите диапазон ячеек С6:С24 и выберите команду Формат → Столбец → Скрыть (рис. 10, результат - рис. 11);
Рис. 10.
Рис. 11.
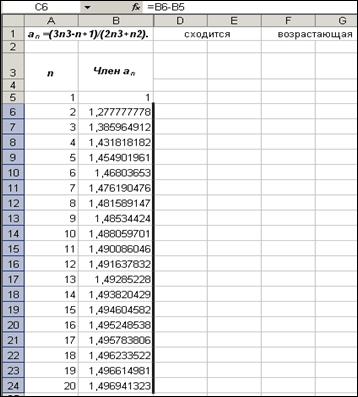
b) выделите строки 6:23 и выберите команду Формат → Строка → Скрыть (рис. 12); c) в ячейку А25 введите =А24*5;
Рис. 12.
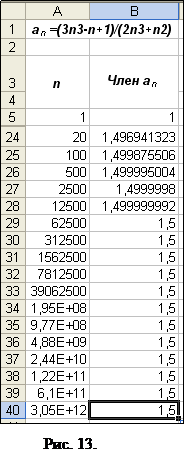
е) активизируйте ячейку В24 и, "зацепив" маркер автозаполнения, протяните его до ячейки В40 (рис. 13);
f) в ячейку А41 введите “lim аn=...”, вместо точек введите соответствующее значение в случае существования такового. Выделите ячейки А41 и В41 и объедините их с помощью кнопки
а) выделить ячейки А5:В24 и выберите команду Формат → Строка → Отобразить. b) На стандартной панели инструментов нажмите на кнопку Мастер Диаграмм c) Выберите диапазон А5:В24 (шаг 2 из 4). Нажмите два раза Далее. На шаге 4 выберите Поместить диаграмму на листе: отдельном. Нажмите Готово. d) Щёлкните по оси Y значений и в появившемся контекстном меню выберите Формат оси. e) На вкладке Шкала в поле минимальное значение укажите 1 (Рис. 16). Нажмите ОК.
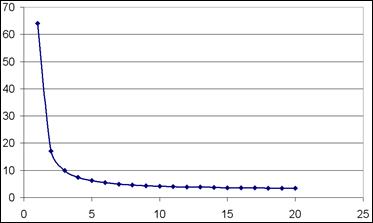
Рис. 16. Анализируя график, можно отметить, что кривая f(n) бесконечно приближается к значению по оси Y в 1,5.
Задания 1. Для последовательности 1) перейдите на новый лист. Для этого поместите указатель мыши на ярлычок листа, с которым вы будете работать (Лист2) и щелкните мышью на нем. Если новых листов больше нет, то вставьте его, выбрав команду Вставка → Лист. После этого добавится новый лист со следующим порядковым номером. Оставьте активной ячейку А1. 2) выберите команду Сервис → Макрос → Макросы, затем в окне диалога Макросы подтвердите выбор Макроса1 и щелкнитена кнопке Выполнить; 3) в ячейку А1 дополнительно введите 4)в ячейку В5 введите формулу первого члена последовательности:=(A5^3-A5-3)/(2*A5^2+A5+1);
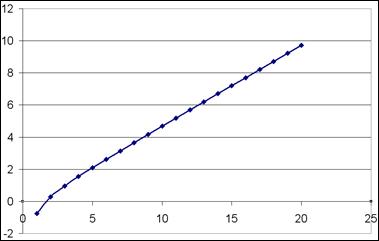
5) выполните последовательно оставшиеся пункты. В качестве ответа вы должны получить график функции f(n). Ответ: 2. Для последовательности
Ответ: 3. Для последовательности
Ответ:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.174.204 (0.008 с.) |

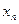 , то множество занумерованных действительных чисел
, то множество занумерованных действительных чисел
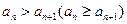 для любого п, и возрастающей (неубывающей), если
для любого п, и возрастающей (неубывающей), если 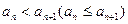 .
.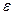 существует номер N, такой что при всех п>N выполняется неравенство
существует номер N, такой что при всех п>N выполняется неравенство 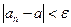 .
.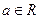 , называют сходящейся, в противном случае расходящейся.
, называют сходящейся, в противном случае расходящейся.
 на панели задач Windows.
на панели задач Windows.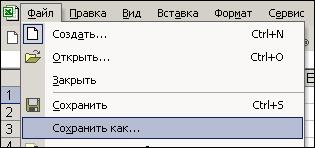
 на стандартной панели инструментов.
на стандартной панели инструментов.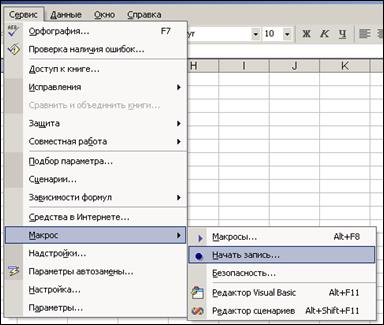
 ;
;
 (объединить и поместить в центре) на панели инструментов форматирования. Затем щелкните на кнопке
(объединить и поместить в центре) на панели инструментов форматирования. Затем щелкните на кнопке  (жирный текст) и кнопке
(жирный текст) и кнопке  (курсив). В строке формул текст отображается не отредактированным;
(курсив). В строке формул текст отображается не отредактированным; ), затем введите n и нажмите Alt + Enter, чтобы поднять текст внутри ячеек. Для активизации ячейки в соседнем столбце справа от A3, нажмите вместо Enter клавишу Tab;
), затем введите n и нажмите Alt + Enter, чтобы поднять текст внутри ячеек. Для активизации ячейки в соседнем столбце справа от A3, нажмите вместо Enter клавишу Tab;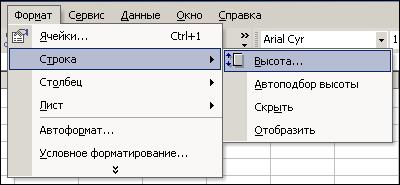
 (остановить запись) на панели Остановка записи;
(остановить запись) на панели Остановка записи;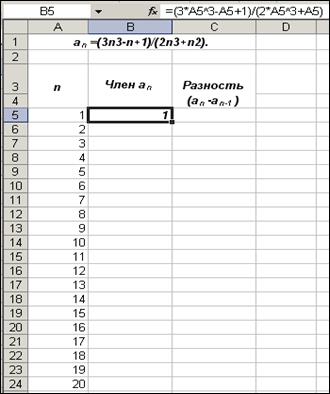
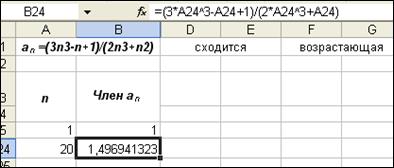
 (жирный текст) и кнопке
(жирный текст) и кнопке  (курсив) (рис. 14);
(курсив) (рис. 14);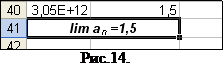
 7. Построим точечную функцию зависимости
7. Построим точечную функцию зависимости 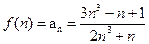 ,
, 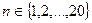 .Для этого необходимо:
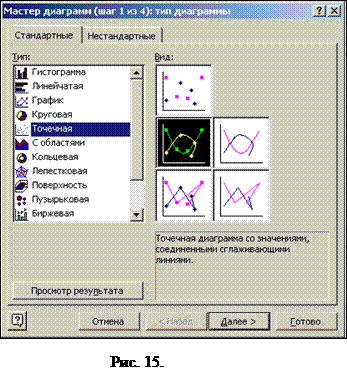
.Для этого необходимо: . В поле Тип выберите Точечная, а в поле Вид выберите второе изображение - шаг 1 из 4 (Рис. 15.) Нажмите Далее.
. В поле Тип выберите Точечная, а в поле Вид выберите второе изображение - шаг 1 из 4 (Рис. 15.) Нажмите Далее.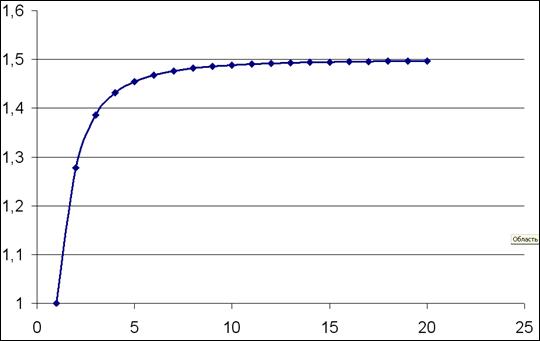
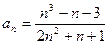 создайте таблицу и постройте график, по аналогии с примером, описанным выше, пользуясь при этом записанным Макросом1 на новом Листе2. С этой целью выполните следующие действия:
создайте таблицу и постройте график, по аналогии с примером, описанным выше, пользуясь при этом записанным Макросом1 на новом Листе2. С этой целью выполните следующие действия: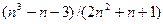 .
.
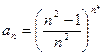 создайте таблицу и постройте график.
создайте таблицу и постройте график.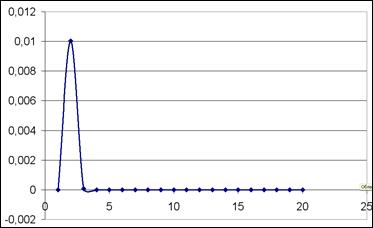
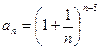 создайте таблицу и постройте график.
создайте таблицу и постройте график.