Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №7. Умножение матриц.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Произведение матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
Пусть даны матрица А размера [ п х т ] и матрица В размера [ т х р ]. Произведением двух матриц А и В, заданных в определённом порядке (А - первая, В - вторая), называется матрица С размера [ п х р ], элементы с ij которой определяются по следующему правилу: элемент i -й строки и j- го столбца матрицы С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j- го столбца матрицы В (рис.43), т.е. c ij = ai1b1 j + ai2b2 j + … + aimbmj = i = 1, 2, …, n; j = 1,2, …, p. Произведение матриц А и В, взятых в указанном порядке, обозначается А·В или АВ.
Произведением двух прямоугольных матриц является снова прямоугольная матрица, число строк которой равно числу строк первой матрицы, а число столбцов – числу столбцов второй матрицы. Из определения умножения матриц видно, что если возможно умножение матрицы А на матрицу В, то отсюда не следует возможность умножения матрицы В на матрицу А. Умножение матриц не обладает свойством перестановочности, поэтому если оба произведения АВ и ВА имеют смысл, то АВ может не совпадать с ВА. В том случае, когда оба произведения АВ и ВА определены и выполняется равенство АВ=ВА, матрицы А и В называют перестановочными. Умножение матриц обладает следующими свойствами: Свойство 1. А(ВС)=(АВ)С Свойство 2. "lÎÂ(l(АВ)=(lА)В=А(lВ)) Свойство 3. С (А+В)=СА+СВ Свойство 4. (А+В)С=АС+ВС Свойство 5. (АВ)Т=ВТАТ , где А,В,С – матрицы, а l – число, а АТ это матрица, полученная из матрицы А в результате транспонирования. Пусть нам даны две матрицы А и В, где матрица А имеет размерность [5х6], а матрица В имеет размерность [6х7].
Тогда, используя формулу (1) получаем:
где с11= 4*(-5)+4*0+(-1) *2+0*6+(-1) *5+8* (3)= -3; с12= 4*(-7)+4*0+(-1)*0+0*4+(-1) *(-4)+8* 0= -24; ……………………………………………………. ……………………………………………………. с56= 1*16+7*0+6*0+6*(-5)+5 *6+7* 0 = 16; с57= 1*1+7*4+6*1+6*5+5 *1+7* 1 = 77.
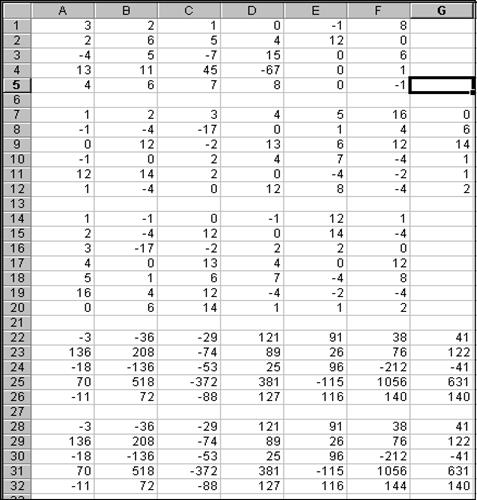
Как видно из примера, вычисление элементов матрицы представляет собой громоздкий процесс, поэтому здесь для подсчёта элементов матрицы С удобно воспользоваться программой Excel. Матрицы А и В необходимо переписать на экран компьютера, для чего войдите в программу Word – 97, после выполнения следующих операций: 1. Включите компьютер. 2. После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Word. 3. Вставьте объект Microsoft Equation 3. 0. 4. Перепишем матрицы А и В в формульном редакторе. Для этого: · Вставьте шаблон матрицы А в формульном редакторе, используя в ШАБЛОНЕ СКОБОК шаблон вида ·Выполните нажатие ЛКМ на кнопке ОПЕРАТОРЫ и выберите шаблон вида · Вставьте шаблон матрицы В в формульном редакторе, используя в ШАБЛОНЕ СКОБОК шаблон вида Выполним вычисления. Для этого воспользуемся инструментами программы Excel. 5. Откройте окно MicrosoftExcel. 6. Перепишите матрицы А и В из Word в Excel (см. рис. 7.2).
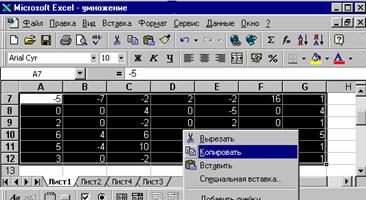
Рис. 7.1 Рис. 7.2 7. Чтобы подсчитать элементы матрицы С, воспользуемся функцией СУММПРОИЗВ, которая находится в мастере функций ƒх и перемножает все компоненты двух массивов, а затем складывает полученные произведения. Но вышесказанную операцию функция может осуществить, если аргументы, которые являются массивами, имеют одинаковые размерности. В нашем примере матрицы А и В имеют разные размерности. Поэтому, чтобы воспользоваться данной функцией, прежде транспонируем матрицу В. Для этого: · активизируйте ячейку А7; · выполните нажатие ЛКМ на ячейке А7 и перетащите курсор по главной диагонали до ячейки G12; · отпустите левую кнопку мыши, при этом область А7¸G12 окажется выделенной. & Далее в тексте задачника будем обозначать: выделите область... ·Выполните нажатие ПКМ, после чего на экране компьютера появится контекстное меню; ·выполните нажатие ЛКМ на слове КОПИРОВАТЬ (рис. 7.3); · активизируйте ячейку А14; ·в строке меню выполните нажатие ЛКМ на кнопке ПРАВКА, а затем в открывшемся контекстном меню выполните то же самое действие на кнопке СПЕЦИАЛЬНАЯ ВСТАВКА (рис. 7.4);
·в открывшемся окне выполните нажатие ЛКМ на Транспонировать (рис. 7.5); ·выполните нажатие ЛКМ на ОК; результат см. на рис. 7.6.
Рис. 7.5 Рис.7.6 В результате проделанных действий на экране Excel появится матрица ВТ (рис. 7.6), при помощи которой мы сможем осуществить поставленную задачу. 8. Вычисления будем производить следующим образом: · активизируйте ячейку А22; · воспользуйтесь функцией СУМПРОИЗВЕД, которая находится в мастере функций ƒх в категории МАТЕМАТИЧЕСКИЕ · для вычисления второго элемента 1-ой строки необходимо ввести в ячейку В22 следующие строки: · формула вычисления 7-го элемента 1-ой строки будет иметь следующий вид: · в ячейке А26 разместим 1-ый элемент последней строки матрицы С: · в ячейке G26 окажется последний элемент последней строки матрицы С:
На рис. 7.7 элементы матрицы С располагаются в ячейках А22¸G26. 9. Быструю проверку проделанных вычислений произведём также в программе Excel. Для этого: ·
· выделите область А28¸G32; · воспользуйтесь функцией МУМНОЖ, которая находится в мастере функций ƒх в категории МАТЕМАТИЧЕСКИЕ, где в окне Массив1 выделите область А1:F5, а в окне Массив2 выберите область А7:G12 (рис. 7.8);
Рис. 7.8 Рис. 7.9 на клавиатуре одновременно нажмите следующую комбинацию клавиш: Shift+Ctrl+Enter. В результате чего в ячейках появятся следующие значения (рис. 7.9). Полученные значения доказывают правильность произведённых вычислений.
& Это полезно знать! Приложение Microsoft Excel в отличие от других приложений пакета Office обладает следующим свойством: если при решении задачи будут постоянно выполняться ссылки на ячейки, то в результате мы получим «шаблон» решения однотипных задач. Например, если при решении описанной выше задачи мы выполним транспонирование матрицы В не так, как описано в п. 7, а следующим образом: 1. Выделим область ячеек А22:G26; 2. воспользуемся функцией ТРАНСП, которая находится в мастере функций fx в категории Ссылки и массивы в появившемся диалоговом окне в поле «Массив» выделим область A7:G12; 3. на клавиатуре одновременно нажмём комбинацию клавиш Shift+Ctrl+Enter. Начиная с п.8 все действия остаются без изменения. В результате, если нам снова придётся находить произведение матриц размерностей [5x6] и [6x7], то автоматически результаты будут выведены на экран. Например, при нахождении произведения матриц
промежуточные вычисления и результат разу же появляются в ячейках электронной таблицы (см. рис. 7.10).
Задания для самостоятельной работы. 1. Найти произведения матриц в Excel.
2. Вычислить АВ и ВА, если
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |






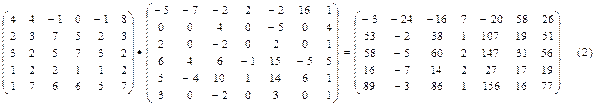
 , а в ШАБЛОНЕ МАТРИЦ шаблон вида
, а в ШАБЛОНЕ МАТРИЦ шаблон вида  (в окне СТОЛБЦОВ выберите число 6, а в окне СТРОК – число 5).
(в окне СТОЛБЦОВ выберите число 6, а в окне СТРОК – число 5). .
.






 ;
; и т.д.;
и т.д.; и т.д.;
и т.д.; ;
;
 При этом в окне программы появятся следующие числа (рис. 7.7):
При этом в окне программы появятся следующие числа (рис. 7.7):