Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 6. Численное дифференцирование степенной функцииСодержание книги
Поиск на нашем сайте
Описание По определению производной функции f(х) в точке х является предел отношения:
Замена производной Рассмотрим несколько способов построения отношения Для этого разделим отрезок
Рис. 32
Точки
Соседние узлы сетки определяются по формулам
Значения функции в узлах обозначим как Заменив производную
получим правую разностную производную, которая определена во всех узлах сетки, кроме последнего узла - правой границы отрезка. Аналогично, заменив производную
получим левую разностную производную, которая определена во всех узлах сетки, кроме нулевого, совпадающего с левой границей отрезка. Во внутренних точках сетки рассмотрим центральную разностную производную по формуле
Сравним все три разностные производные с производной, вычисленной по аналитической формуле. Для этого рассмотрим для каждой разностной производной погрешность приближения, называемую также погрешностью аппроксимации
Чтобы оценить величину погрешности аппроксимации, разложим функцию
Из формулы (8), используя введенные обозначения, получим формулу
Разделив на h и используя (4), придем к выражению
Правая часть формулы (10) стремится к нулю при
где Аналогично из формулы (9) получим оценку
Вычитая из формулы (8) формулу (9) и поделив полученное выражение на 2h, получим формулу
откуда
Исходя из полученных формул, можно сделать следующие выводы: 1) с уменьшением шага каждая разностная производная будет точнее описывать производную, хотя для расчета производной на всем интервале потребуется сетка с большим числом узлов; 2) так как дать приближенное значение производной в обеих граничных точках ни одна формула не может, то, чтобы рассчитать производную на каком-то отрезке 3) на основе оценок (11), (12) формулы правой и левой разностной производной считаются формулами первого порядка точности по h, т.е., используя O символику можно записать
а формула центральной разностной производной на основе оценки (13) считается формулой второго порядка точности по h:
тем самым более точными.
Возьмем некоторую функцию из таблицы производных, например, функцию
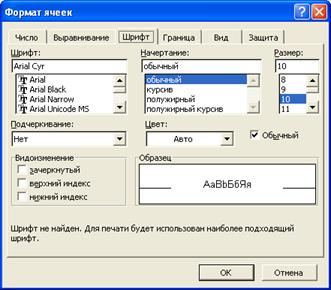
рассчитаем приближенно ее производную различными способами на отрезке Для выполнения задания § осуществите запуск программы Excel, щелкнув на кнопке ПУСК на панели задач и выбрав соответствующий пункт каскадного меню; § в открывшемся рабочем листе (ЛИСТ 1) новой рабочей книги выполните следующие пункты. Создание таблицы значений. 1. Создание строки заголовков. Запишите информацию в строку заголовков таблицы (см. рис. 33). При введении текста следует помнить, что a. для того чтобы ввести информацию в ячейку, необходимо предварительно выделить ее, щелкнув на ней левой кнопкой мыши; b. перенос в ячейке текста на другую строку осуществляется с помощью нажатия сочетания клавиш Alt+Enter; c. для записи верхнего (нижнего) индекса нужно выбрать команду меню ФОРМАТ - ЯЧЕЙКИ, а в раскрывшемся диалоге щелкнуть на корешке вкладки ШРИФТ и щелчком выбрать опцию Верхний (Нижний) индекс, нажать кнопку ОК (см. рис. 34); d. поскольку запись в ячейке F1 похожа на запись в ячейке Е1 удобно сначала скопировать содержание ячейки Е1, а потом внести изменения. Копирование может быть осуществлено многими способами. Например, выделив ячейку Е1, выполните команду ПРАВКА - КОПИРОВАТЬ (см. рис. 35), а потом, выделив ячейку F1, выполнить команду ПРАВКА - ВСТАВИТЬ. Аналогично можно поступить при записи информации в другие ячейки. 2. Вычисление шага сетки по числу интервалов разбиения. В ячейки А2, A3, А4 запишите значения, соответствующие границам отрезка [0; 1,1] и числу интервалов разбиения: 0; 1,1; 11, а в ячейке А5 рассчитайте значение шага h по формуле (2), т.е. запишите формулу Excel: =(А3-А2)/А4 (17) и нажатием клавиши Enter пошлите на выполнение. В результате значение шага - 0.1, а в строке формул - формула (17). Знак равенства в (17) отличает ввод формулы, по которой следует провести вычисление, от ввода текста.
Рис. 33
Рис. 34
Рис. 35
3. Вычисление значений аргумента. В ячейку В2 запишите формулу Excel: =A2 и нажмите Enter. В ячейке В2 появится значение левого края отрезка. В дальнейшем, при изменении числового значения в ячейке А2, будет изменяться число и в В2. В ячейку ВЗ запишите значение следующей точки оси Х по формуле Excel: =B2+A5 и закрепите в ней адрес шага сетки h - ячейку А5. Для этого дважды щелкните мышью в строке формул на адресе А5, чтобы выделить его, и нажмите клавишу F4. После этого адрес ячейки А5 станет абсолютным, на что указывает символ $ перед буквой столбца и номером строки адреса. Формула примет вид =В2+$А$5 (18) В дальнейшем, при переносе формулы адрес А5, в отличие от адреса В2, меняться не будет. Нажмите Enter. Установите курсор мыши на маркере заполнения ячейки ВЗ, т.е. на маленьком черном квадратике в правом нижнем углу ячейки ВЗ (см. рис. 36). При этом указатель мыши примет вид черного крестика. В этом положении курсора нажмите левую кнопку мыши и, не отпуская ее, перетащите курсор вниз до ячейки В13, соответствующей правому концу отрезка, и отпустите кнопку мыши. После выполнения этого действия столбец В таблицы будет заполнен значениями точек разбиения отрезка [0; 1,1].
Рис. 36 Чтобы понять, как изменяется формула (18) при выполненном переносе, щелкните на некоторых ячейках столбца В и рассмотрите формулы, которые высветятся в строке формул. 4. Вычисление значений функции. В ячейку С2 запишите формулу Excel: =B2^4, по которой рассчитывается значение функции (16) в точке В2 и нажмите Enter. Перенесите эту формулу ячейки С2 вниз до тринадцатой строки с помощью маркера заполнения также, как это сделано в пункте 3. После выполнения этого шага в столбце С таблицы окажутся значения функции (16) во всех узлах сетки. 5. Вычисление значений производной функции. В ячейку D2 запишите формулу Excel: =4*B2^3, по которой рассчитывается значение производной функции (16) в точке В2, нажмите Enter и перенесите формулу ячейки D2 вниз до тринадцатой строки с помощью маркера заполнения. После выполнения этого шага в столбце D таблицы окажутся значения производной функции (16) в узлах сетки. 6. Численное дифференцирование функции с помощью формулыправой разностной производной (4): В ячейку Е2 запишите формулу Excel: =(СЗ-С2)/$А$5, (19) по которой рассчитывается значение правой разностной производной (4) в точке В2. Адрес ячейки А5 в формуле (18) закрепляется также как в пункте 3. С помощью маркера заполнения перенесите формулу ячейки Е2 вниз до двенадцатой строки, соответствующей точке разбиения с номером n-1. После выполнения этого шага в столбце Е окажутся значения правой разностной производной функции (16) в узлах сетки. Ячейка Е13 при этом остается пустой, так как соответствует правому концу отрезка, где правая разностная производная не вычисляется. 7. Численное дифференцирование функции с помощью формулы левой разностной производной (5): При вычислении левых разностных производных ячейка F2 остается пустой, так как соответствует левому концу отрезка, где левая разностная производная не вычисляется. В ячейке F3 значение левой разностной производной (5) в точке ВЗ вычисляется по той же формуле (19). С помощью маркера заполнения перенесите формулу ячейки F3 вниз опять до тринадцатой строки, соответствующего точке с номером n. После выполнения этого шага в столбце F окажутся значения левой разностной производной функции (16) в узлах сетки. 8. Численное дифференцирование функции с помощью формулы центральной разностной производной (6): При вычислении центральных разностных производных остаются пустыми ячейки F2 и Е14, соответствующие левому и правому концам отрезка. В ячейку G3 запишите формулу вычисления значение центральной разностной производной (6) в точке ВЗ: =(С4-С2)/$А$5/2 (20) нажмите Enter и с помощью маркера заполнения перенесите формулу ячейки G3 вниз до двенадцатой строки. 9. Вычисление абсолютных погрешностей. Погрешности будем вычислять только в точках отрезка [0,1; 1,0]. Выделите ячейку H3 и, нажав клавишу =ABS(D3-E3) (21) и нажмите Enter. В результате вычистится погрешность d1 в ячейке ВЗ. Погрешность d2 в ячейке I3 следует вычислить по формуле =ABS(D3-F3), a погрешность d3 в ячейке J3 - по формуле =ABS(D3-G3). Поскольку эти формулы аналогичны (21), то удобно не выполнять повторно команду ВСТАВКА ФУНКЦИИ, а скопировать содержимое ячейки НЗ в ячейки I3 и J3 и изменить адреса ячеек в формуле (21). Копировать можно через буфер, как описано в пункте 1. По другому способу требуемые команды копирования можно вызвать, нажав правую кнопку мыши, т.е. вызвав контекстное меню. Выделите три ячейки: НЗ, I3 и J3 ВЗ:В13, т.е. проведите по этим ячейкам курсором мыши, держа левую кнопку нажатой, и отпустите кнопку. С помощью маркера заполнения перенесите формулы всех трех ячеек одновременно вниз до двенадцатой строки, соответствующей последней точке отрезка [1; 2]. 10 Вычисление относительных погрешностей аппроксимации. В ячейки K3,L3,M3 запишите формулы =H3/D3, =I3/D3, =J3/D3 соответственно. Выделите эти три ячейки, и с помощью маркера заполнения перенесите формулы всех трех ячеек одновременно вниз до двенадцатой строки. В результате выполненных шагов получится таблица:
Рис. 37
11. Анализ погрешностей. Значения погрешностей показывают близость к аналитической производной любой из трех разностных производных. Хотя абсолютные погрешности и растут с увеличением значения функции, относительные погрешности уменьшаются. Сравнение погрешностей показывает, что наиболее точные значения производной дает центральная разностная формула, как и следует из теории (вывод 3 Описания). Для наглядности построим графики всех производных. Построение графиков. Для построения графиков функций 1. Выделите с помощью мыши блок ячеек D1:G1 и нажмите сочетание клавиш Shift+F8. В результате в строке состояния появится сообщение ДОБ, означающее, что следующие выделенные ячейки будут добавлены к уже выделенным (см. рис. 38). Выделите блок ячеек D3:G12.
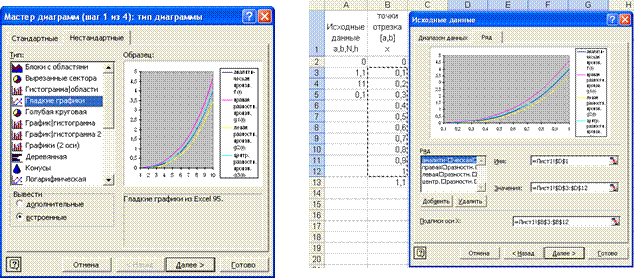
Рис. 38 2. Вызовите МД нажатием кнопки 3. Щелкните на корешке вкладки НЕСТАНДАРТНЫЕ и в левом окне ТИП выберите гладкие графики, после чего в правом окне появится образец графика, в котором по оси абсцисс будут стоять номера точек (см. рис. 39). Перейдите на следующий шаг, нажав кнопку Далее.
Рис. 39 Рис. 40
4. На втором шаге МД, указывающем источник данных, на вкладке ДИАПАЗОН ДАННЫХ проверьте адреса выделенных ячеек. При этом ряды должны быть размещены в столбцах. Щелкните на корешке вкладки РЯД и в поле "ПОДПИСИ ОСИ X:". После этого выделите на Листе1 Excel блок ячеек ВЗ:В12, т.е. проведите по этим ячейкам курсором мыши, держа левую кнопку нажатой, и отпустите кнопку. В результате данный блок ячеек будет выделен пунктирной рамкой, в поле "ПОДПИСИ ОСИ X:" появятся адреса этих ячеек, а в образце графика - правильные значения точек по оси абсцисс (рис. 40). Перейдите на следующий шаг МД, нажав кнопку Далее. 5. На третьем шаге МД, указывающем параметры диаграммы, на вкладке ЗАГОЛОВКИ в поле "НАЗВАНИЕ ДИАГРАММЫ" запишите "Производные при h=0,1" и нажмите кнопку Готово. В результате на Листе1 появится диаграмма с требуемыми графиками. Данная диаграмма будет выделена, на что указывают черные квадратики - "ручки" - по углам и в середине сторон рамки диаграммы. 6. Поместите диаграмму под таблицей и растяните ее. Для этого щелкните мышью на свободном месте области диаграммы, не отпуская мышь, перетащите пунктирную рамку диаграммы под таблицу и отпустите мышь. После этого, взявшись за "ручки", растяните рамку диаграммы так, чтобы она заняла левую половину экрана по ширине и во весь экран высоте. Для перехода в режим во весь экран выполните команду с этим именем в меню ВИД. 7. Щелкнув на области построения графиков, выделите ее и растяните, взявшись за появившиеся "ручки", по ширине и высоте внутри области диаграммы насколько возможно. Полученные графики показаны на рисунке 41. На этом рисунке графики разных разностных производных различаются не цветом, а маркировкой. Сравнение графиков на рисунке 41 наглядно демонстрирует насколько хорошо те или иные разностные аппроксимации близки к точной, аналитически посчитанной производной. Видно, что центральная разностная производная почти точно описывает аналитическую производную. Левая и правая производные дают примерно равные ошибки, но в разные стороны.
Рис. 41
Сохраните полученные результаты, для чего: § в меню ФАЙЛ выберите команду СОХРАНИТЬ КАК...; § в открывшемся диалоговом окне СОХРАНЕНИЕ ДОКУМЕНТА с помощью соответствующих кнопок (см. рис.11) и полосы прокрутки основного окна найдите и поместите в окно "ПАПКА" папку, указанную преподавателем (например, папку с вашей фамилией); § в окне "ИМЯ ФАЙЛА:" запишите имя файла, указанное преподавателем (например "производные"); § 4. проверьте, чтобы в окне "ТИП ФАЙЛА:" было записано "Книга Microsoft Excel (*.xls); § нажмите кнопку СОХРАНИТЬ.
 

Рис. 42
Завершите работу в Excel, нажав крайнюю правую кнопку в строке заголовка.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.50.1 (0.014 с.) |

 (1)
(1) некоторым отношением
некоторым отношением  дает приближенное значение
дает приближенное значение  .
. точками
точками  на n равных частей так, что
на n равных частей так, что  (рис. 32) и
(рис. 32) и  (2)
(2) X0=a x1 x2 x3 xi-1 xi xi+1 xn-1 xn=b
X0=a x1 x2 x3 xi-1 xi xi+1 xn-1 xn=b
 называется узлом или точкой сетки, а величина h - шагом сетки. Тогда
называется узлом или точкой сетки, а величина h - шагом сетки. Тогда , где
, где  (3)
(3) ,
, 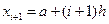
 .
.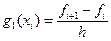 ,
,  (4)
(4) ,
,  , (5)
, (5) ,
,  . (6)
. (6) ,
, 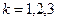 . (7)
. (7) в ряд Тейлора в зафиксированной точке
в ряд Тейлора в зафиксированной точке  , (8)
, (8) . (9)
. (9)
 ,
, 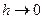 , т.е. является бесконечно малой функцией. Тогда при достаточно малых h для погрешности аппроксимации производной правой разностной производной можно сделать оценку
, т.е. является бесконечно малой функцией. Тогда при достаточно малых h для погрешности аппроксимации производной правой разностной производной можно сделать оценку ,
, 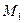 - некоторая постоянная, зависящая от вида функции
- некоторая постоянная, зависящая от вида функции  ,
, 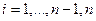 . (12)
. (12)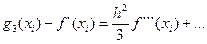 ,
,  ,
,  , нужно рассмотреть отрезок
, нужно рассмотреть отрезок  , включающий
, включающий 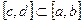 ;
; ,
,  , (14)
, (14) , (15)
, (15) , (16)
, (16) в 10 точках: 0,1; 0,2; 0,3;... 0,9; 1,0 и сравним с производной, вычисленной аналитически. Чтобы рассчитать разностные производные по всем трем формулам в конечных точках отрезка, надо рассмотреть больший отрезок (см. вывод 2 Описания). Для этого рассмотрим отрезок
в 10 точках: 0,1; 0,2; 0,3;... 0,9; 1,0 и сравним с производной, вычисленной аналитически. Чтобы рассчитать разностные производные по всем трем формулам в конечных точках отрезка, надо рассмотреть больший отрезок (см. вывод 2 Описания). Для этого рассмотрим отрезок  . Разобьем его на 11 одинаковых интервалов, получим равномерную сетку с шагом h =0.1, в узлах которой построим разностные производные
. Разобьем его на 11 одинаковых интервалов, получим равномерную сетку с шагом h =0.1, в узлах которой построим разностные производные 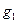 ,
,  ,
, 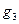 по формулам (4), (5), (6). Все требуемые вычисления и построения графиков описаны ниже для пакета Excel 97.
по формулам (4), (5), (6). Все требуемые вычисления и построения графиков описаны ниже для пакета Excel 97.



 в точках i=1,...,n.
в точках i=1,...,n. на панели инструментов, выполните команду ВСТАВКА ФУНКЦИИ. В левом окне открывшегося диалога выберите категорию функций математические, а в правом окне - функцию ABS. После этого в строке формул в скобках наберите D3-E3 (щелкнув мышью на указанных ячейках). Получится формула
на панели инструментов, выполните команду ВСТАВКА ФУНКЦИИ. В левом окне открывшегося диалога выберите категорию функций математические, а в правом окне - функцию ABS. После этого в строке формул в скобках наберите D3-E3 (щелкнув мышью на указанных ячейках). Получится формула
 ,
, 
 . Появится диалоговое окно первого шага, в котором определяется тип диаграммы.
. Появится диалоговое окно первого шага, в котором определяется тип диаграммы.